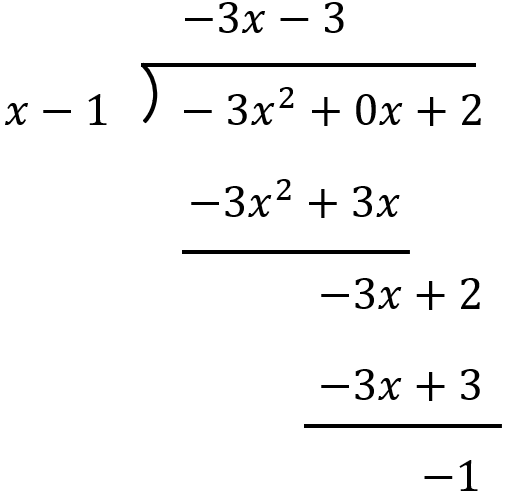As assíntotas de uma função são valores que uma função se aproxima à medida que os valores de x se aproximam de um valor específico. Por exemplo, uma função pode se aproximar, mas nunca atingir o eixo x quando os valores de x tendem ao infinito.
A seguir, veremos um resumo dos três tipos de assíntotas que as funções podem ter. Além disso, veremos vários exercícios de assíntotas resolvidos para aprender como encontrar as assíntotas de funções.
Resumo e exercícios de assíntotas verticais
Para encontrar as assíntotas verticais de uma função, temos que examinar os fatores do denominador que não são comuns aos fatores do numerador. Os zeros desses fatores representam as assíntotas verticais.
Podemos usar os seguintes passos para identificar as assíntotas verticais de funções racionais:
Passo 1: Se possível, fatorar o numerador e o denominador.
Passo 2: Determine se o domínio da função tem alguma restrição.
Passo 3: Cancele os fatores comuns, se houver, para simplificar para a expressão.
Passo 4: Se houver um valor na versão simplificada que torne o denominador zero, esses valores representam as assíntotas verticais.
EXERCÍCIO 1
Considerando a função racional $latex f(x) =\frac{{{x}^2}+2x-3}{{{x}^2}-5x-6}$, encontre suas assíntotas verticais.
Solução: podemos fatorar o numerador e o denominador da seguinte forma:
$latex f(x)=\frac{(x+3)(x-1)}{(x-6)(x + 1)}$
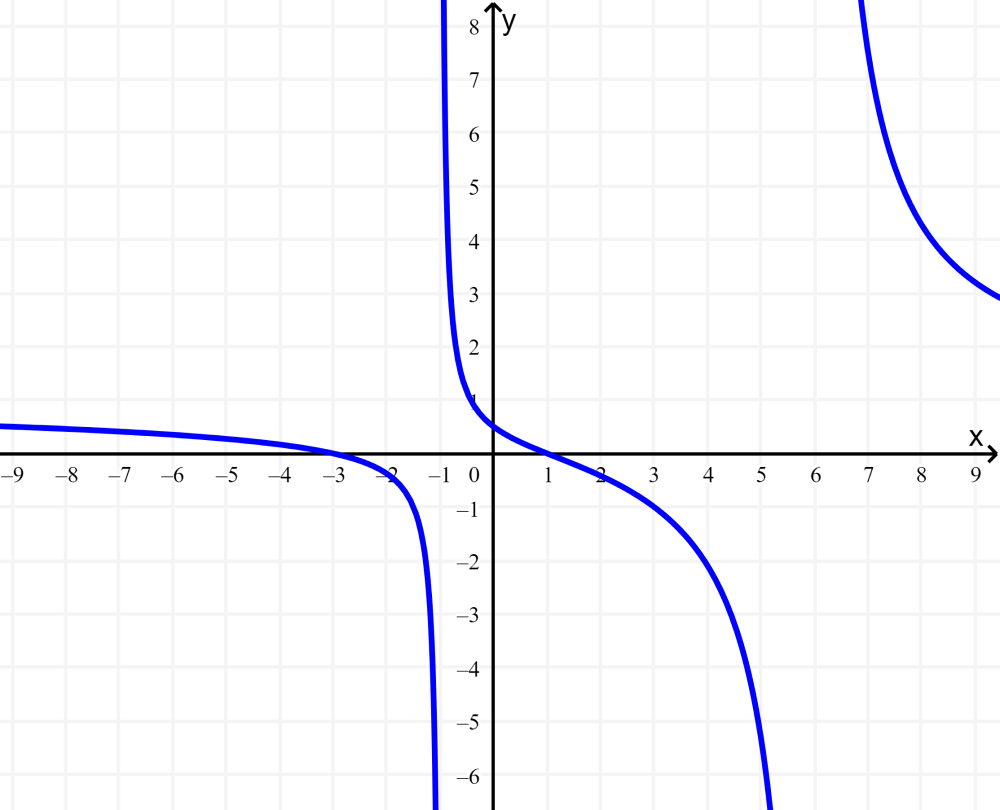
Olhando para o denominador, sabemos que x não pode ser nem 6 nem -1, pois teríamos divisão por zero. A seguir está o gráfico da função racional:
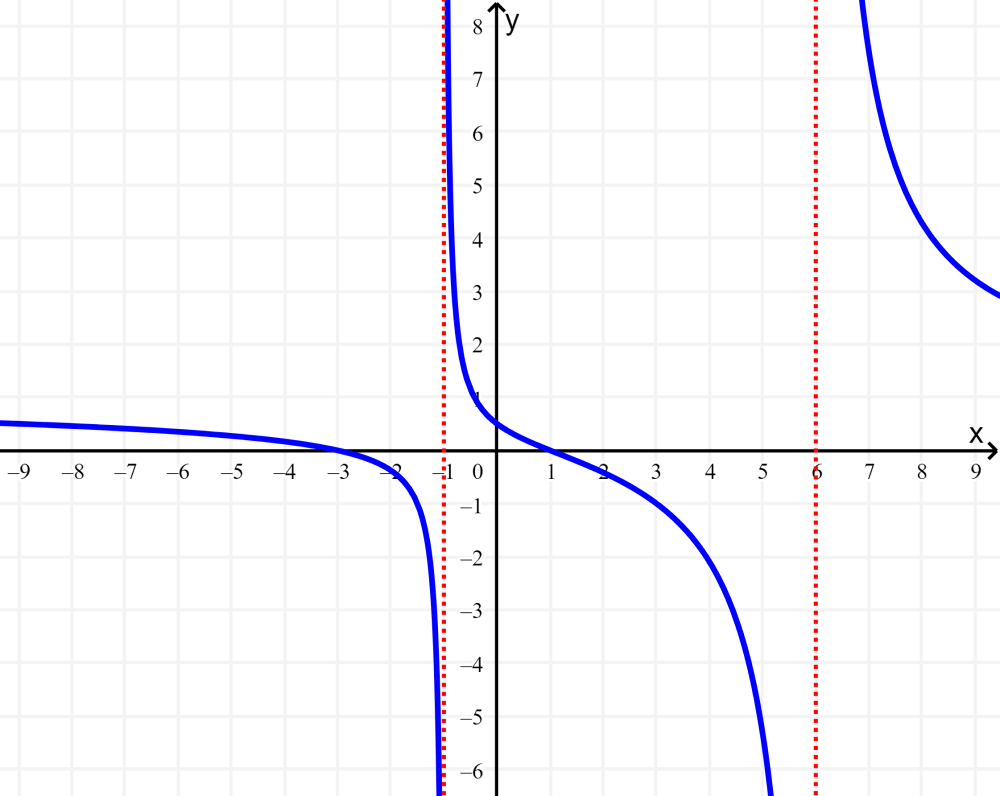
No gráfico, vemos que as curvas evitam as linhas verticais $latex x=6$ e $latex x=-1$. Os valores de x não podem ser iguais a 6 ou -1, portanto, essas são as assíntotas. Podemos desenhar as assíntotas verticais como linhas tracejadas:
EXERCÍCIO 2
Dada a função $latex g(x)=\frac{x+2}{{{x}^2}+2x-8}$, encontre suas assíntotas verticais.
Solução: Aqui, só temos que fatorar para o denominador:
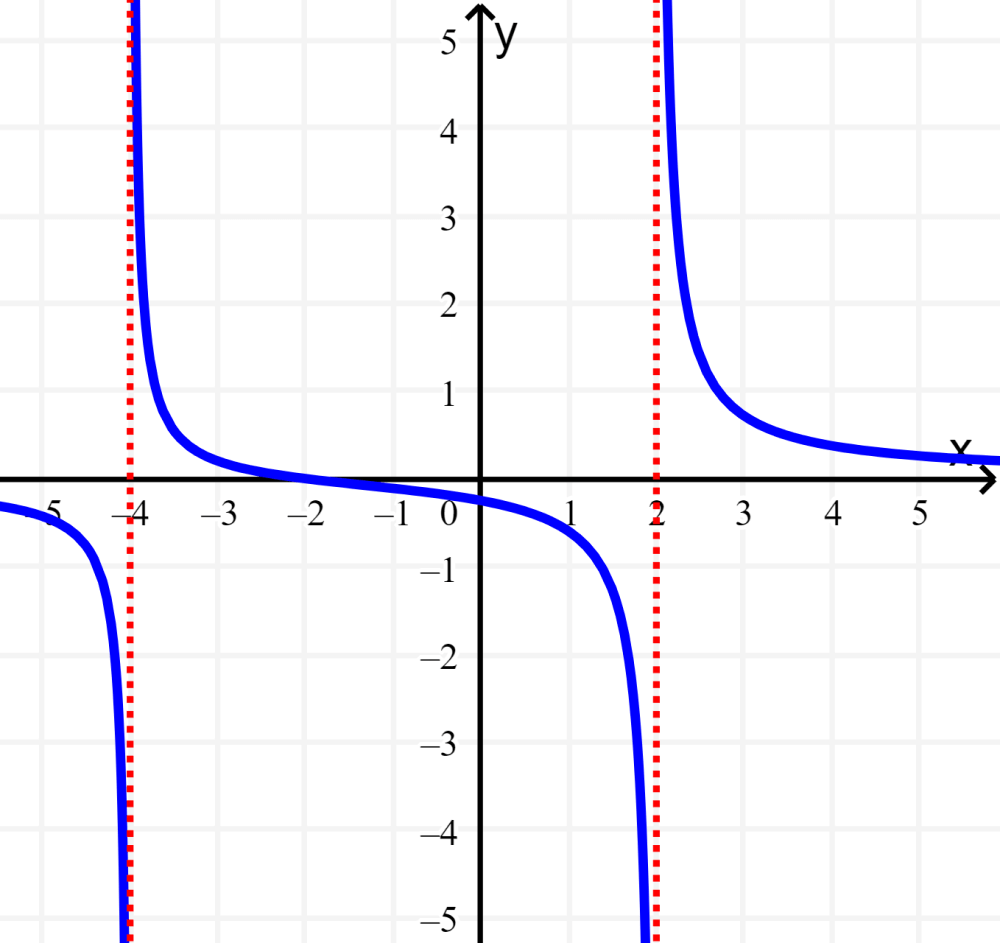
$latex f(x)=\frac{x+2}{(x+4)(x-2)}$
Olhando para o denominador, sabemos que x não pode ser igual a $latex x=-4$ ou $latex x=2$, pois isso causaria a divisão por zero. Isso nos diz que as assíntotas verticais da função estão localizadas em $latex x=-4$ e $latex x=2$:
Experimente você mesmo – Resolva o exercício
Resumo e exercícios de assíntotas horizontais
Para encontrar as assíntotas horizontais de funções racionais, podemos usar os seguintes métodos que variam dependendo de como os graus do polinômio se comparam no numerador e denominador da função:
• Quando o grau do polinômio no numerador é igual ao grau do polinômio no denominador, dividimos os coeficientes líderes (da variável com o maior expoente) para obter as assíntotas horizontais.
• Quando o grau do numerador é menor que o grau do denominador, temos a assíntota horizontal $latex y=0$.
• Quando o grau do numerador é maior que o grau do denominador, a função não tem assíntotas horizontais.
Vamos ver alguns exercícios:
EXERCÍCIO 1
Dada a função $latex g(x)=\frac{x+2}{2x}$, determine suas assíntotas horizontais.
Solução: Tanto no numerador quanto no denominador, temos um polinômio de grau 1. Assim, encontramos a assíntota horizontal considerando os coeficientes de x.
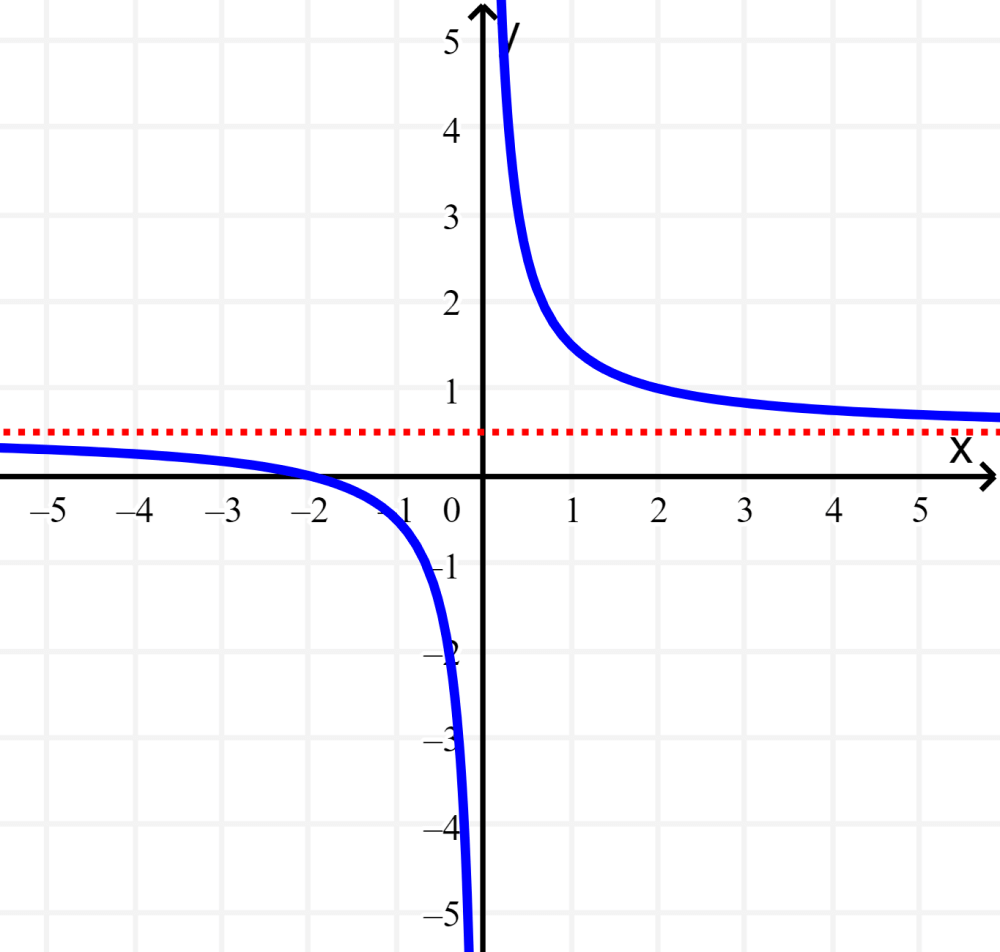
Portanto, a assíntota horizontal da função é $latex y=\frac{1}{2}$:
EXERCÍCIO 2
Dada a função $latex g(x) = \frac{x}{{{x}^2}+2}$, determine suas assíntotas horizontais.
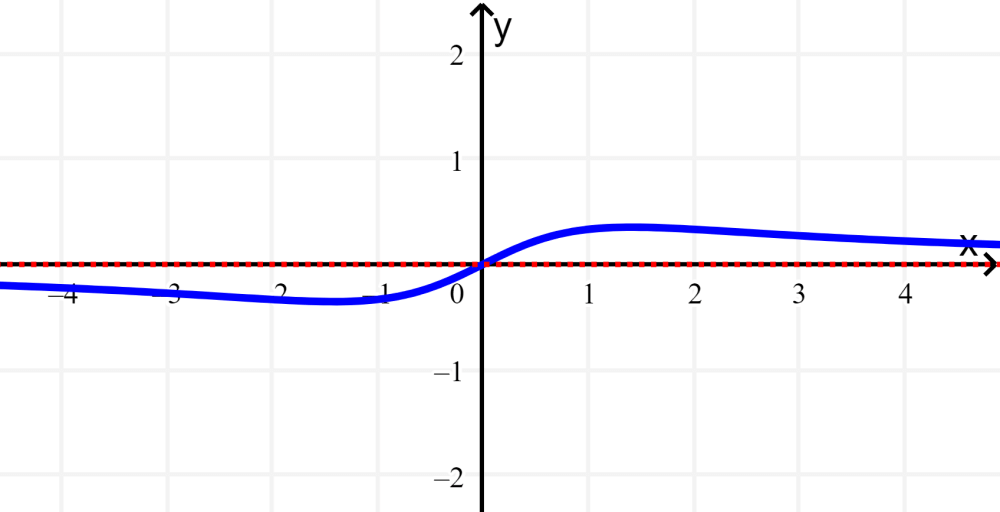
Solução: Nesta função, o grau do numerador é menor que o grau do denominador. Isso significa que a assíntota horizontal está localizada em $latex y=0$:
EXERCÍCIO 3
Dada a função $latex f(x)=\frac{{{x}^2}+2}{x+1}$, encontre suas assíntotas horizontais.
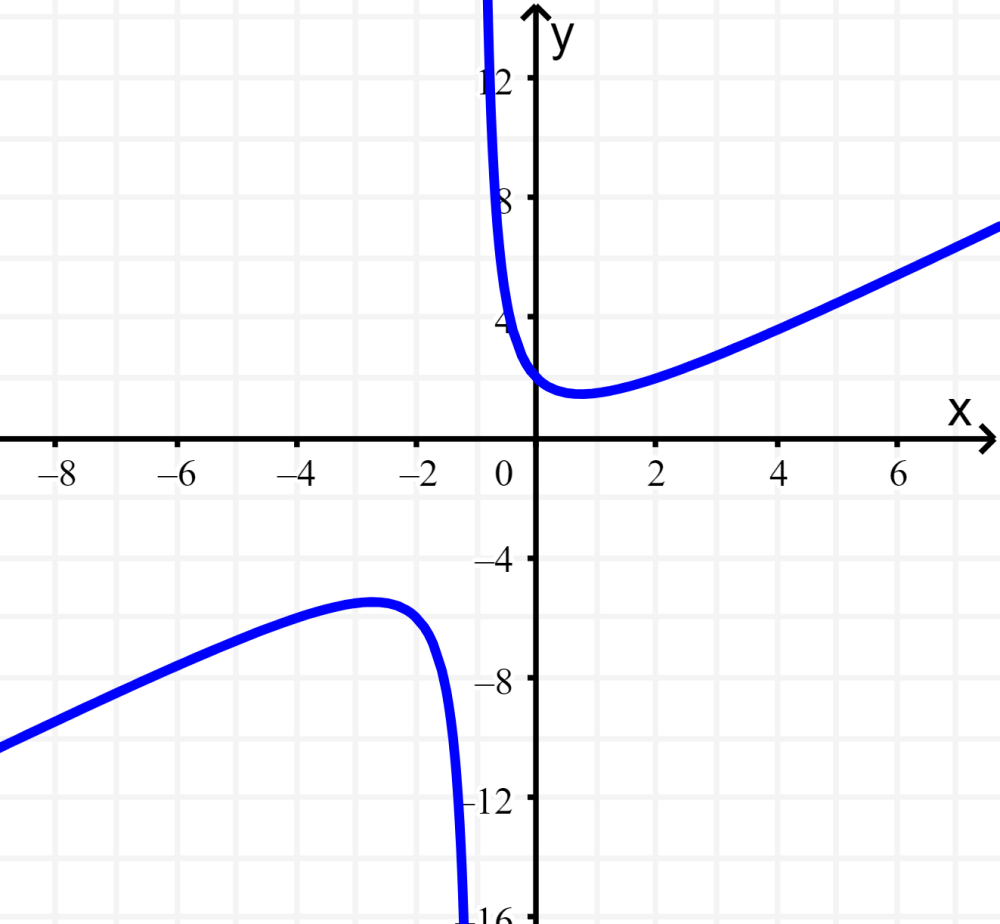
Solução: Vemos que o grau do numerador é maior que o grau do denominador. Isso significa que a função não possui uma assíntota horizontal:
Experimente você mesmo – Resolva os exercícios
Resumo e exercícios de assíntotas oblíquas
As assíntotas oblíquas, também chamadas inclinadas, podem ser determinadas comparando o grau do numerador e o grau do denominador. Quando o grau do numerador é exatamente um a mais que o grau do denominador, a função racional produzirá um gráfico que se parecerá mais ou menos com uma linha inclinada com divergências complicadas no meio. A assíntota desse tipo de função é chamada de assíntota oblíqua ou inclinada.
Para obter a equação desta assíntota, devemos realizar a divisão longa dos polinômios. A equação da assíntota é a parte inteira do resultado da divisão.
EXERCÍCIO 1
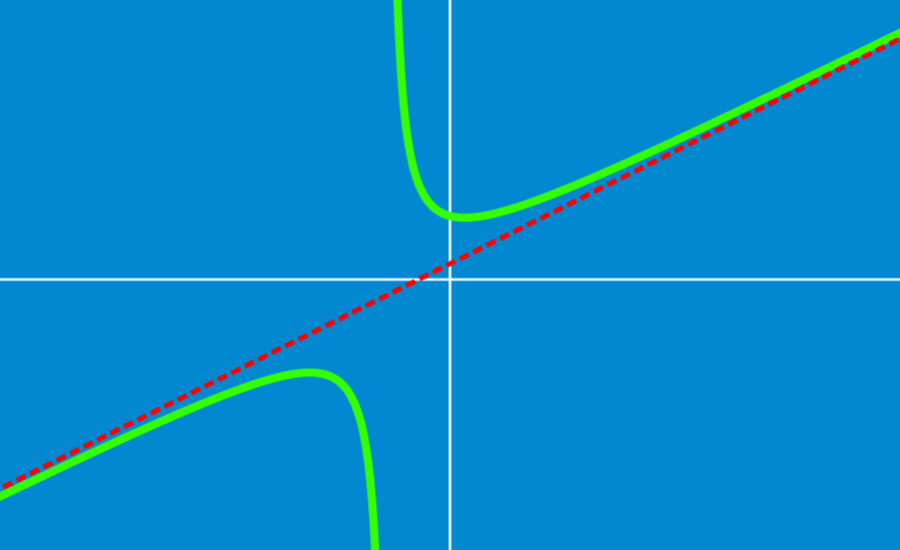
Dada a função $latex f(x) = \frac{-3{{x}^2}+2}{x-1}$, determine sua assíntota oblíqua.
Solução: Temos que realizar a longa divisão desta função racional:
O quociente da divisão, localizado no topo, é a expressão linear $latex -3x-3$. O resíduo está localizado na parte inferior. Portanto, após a divisão, convertemos a função em uma expressão mista:
$latex f(x)=-3x-3+\frac{-1}{x-1}$
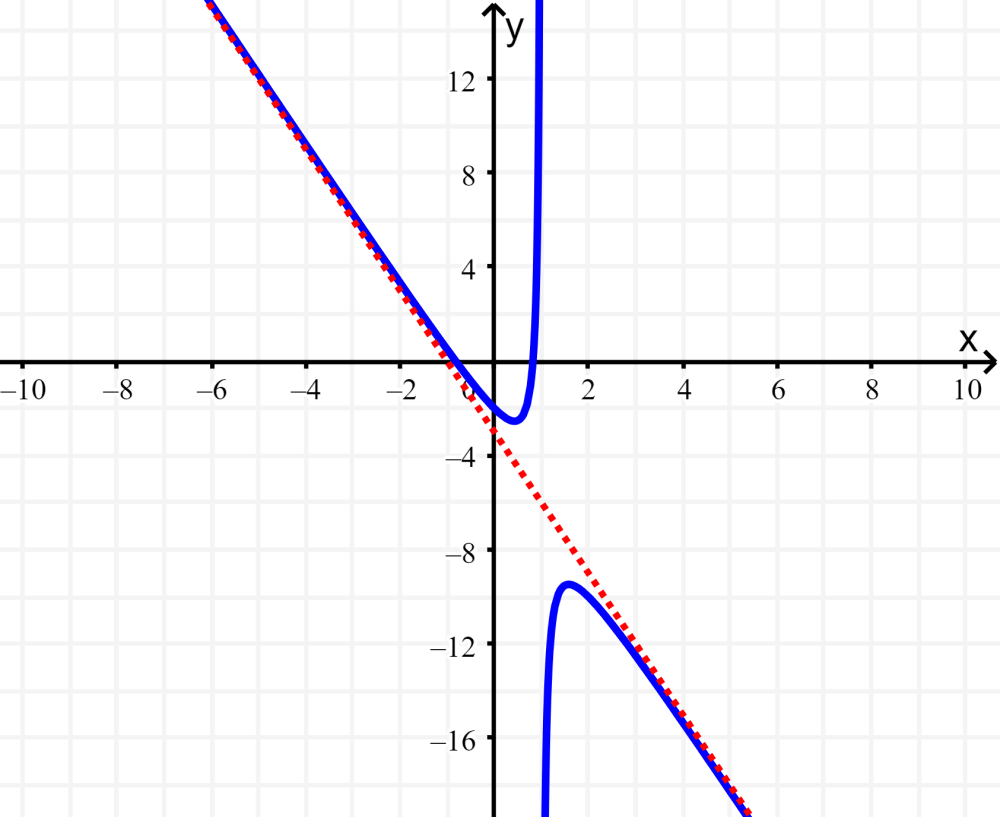
A assíntota oblíqua da função é a linha $latex y=-3x-3$, ou seja, a parte inteira da divisão:
Experimente você mesmo – Resolva o exercício
Veja também
Você quer aprender mais sobre funções racionais e assíntotas ? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
