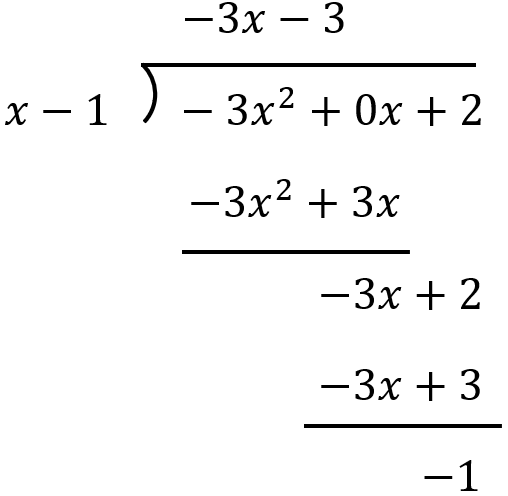As assíntotas de uma função podem ser calculadas investigando o comportamento do gráfico da função. No entanto, também é possível determinar se a função tem assíntotas ou não sem usar o gráfico da função. O método para calcular as assíntotas varia dependendo se a assíntota é vertical, horizontal ou oblíqua.
A seguir, veremos como calcular as assíntotas de uma função com exemplos.
Como calcular as assíntotas verticais de uma função?
As assíntotas verticais de uma função podem ser encontradas examinando os fatores do denominador que não são comuns com os fatores do numerador. As assíntotas verticais ocorrem nos zeros desses fatores.
Dada uma função racional, podemos identificar as assíntotas verticais seguindo estos passos:
Passo 1: Fatorar o numerador e o denominador.
Passo 2: Observe todas as restrições no domínio da função.
Passo 3: Reduza a expressão cancelando os fatores comuns no numerador e denominador.
Passo 4: Encontre qualquer valor que torne o denominador zero na versão simplificada. É aqui que ocorrem as assíntotas verticais.
EXEMPLO 1
Encontre as assíntotas verticais da função racional $latex f(x)=\frac{{{x}^2}+2x-3}{{{x}^2}-5x-6}$.
Solução: Começamos fatorando o numerador e o denominador:
$latex f(x)=\frac{(x+3)(x-1)}{(x-6)(x+1)}$
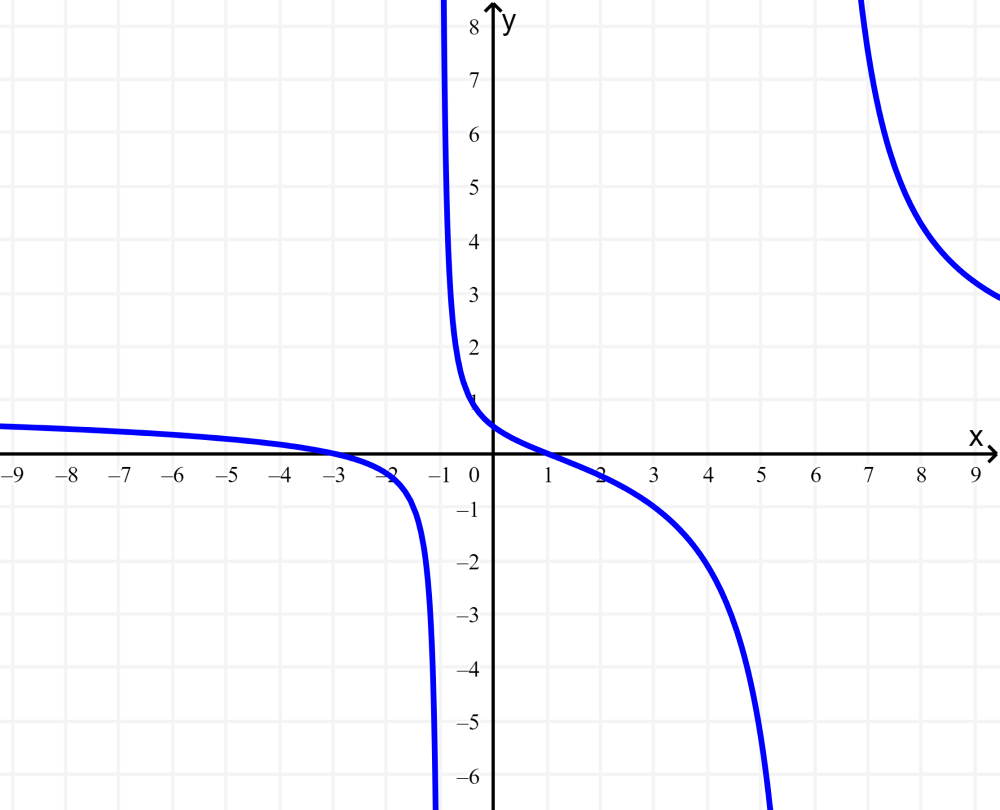
Esta função não pode mais ser simplificada. Portanto, x não pode ser 6 ou -1, pois estaríamos dividindo por zero. Vejamos o gráfico desta função racional:
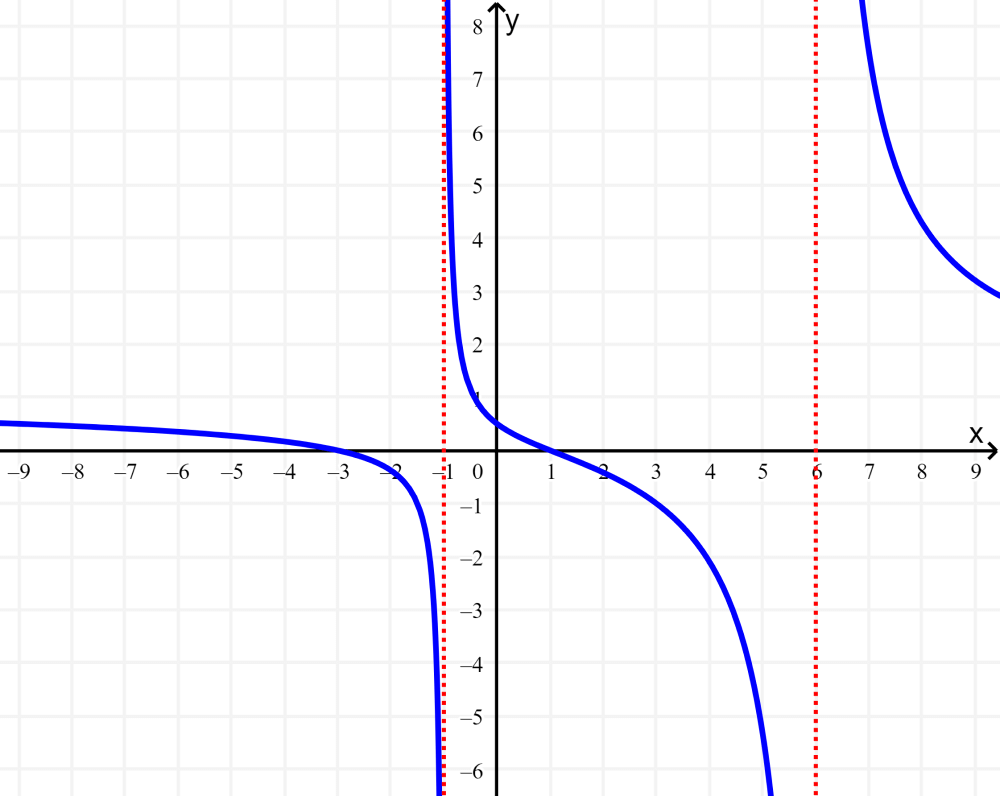
Podemos ver que o gráfico evita as linhas verticais $latex x=6$ e $latex x=-1$. Isso ocorre porque x não pode ser igual a 6 ou -1. Então, desenhamos as assíntotas verticais como linhas tracejadas:
EXEMPLO 2
Encontre as assíntotas verticais da função $latex g(x)=\frac{x+2}{{{x}^2}+2x-8}$.
Solução: O numerador já está fatorado, então fatoramos para o denominador:
$latex f(x)=\frac{x+2}{(x+4)(x-2)}$
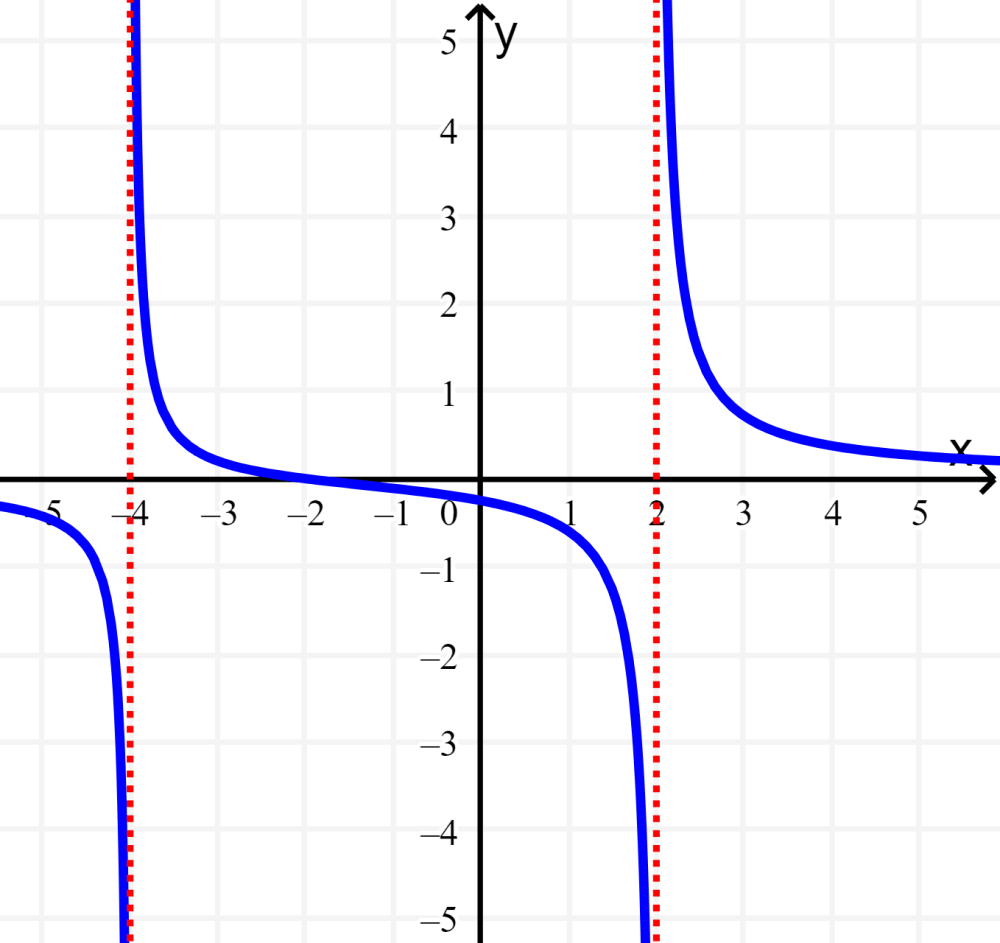
Não podemos simplificar esta função e sabemos que não podemos ter zero no denominador, então x não pode ser igual a $latex x=-4$ ou $latex x=2$. Isso nos diz que as assíntotas verticais da função estão localizadas em $latex x=-4$ e $latex x=2$:
Experimente você mesmo – Resolva os exercícios
Como as assíntotas horizontais são calculadas?
O método para a identificação de assíntotas horizontais muda de acordo com a forma como os graus do polinômio comparar no numerador e denominador da função. Para encontrar as assíntotas horizontais, devemos lembrar o seguinte:
- Se o grau do polinômio do numerador for igual ao grau do polinômio do denominador, dividimos os coeficientes dos termos de maior grau para obter as assíntotas horizontais.
- Se o grau do numerador for menor que o grau do denominador, as assíntotas horizontais serão $latex y=0$.
- Se o grau do numerador for maior que o grau do denominador, não há assíntotas horizontais.
Vejamos alguns exemplos:
EXEMPLO 1
Encontre as assíntotas horizontais da função $latex g(x)=\frac{x+2}{2x}$.
Solução: Como o maior grau no numerador e no denominador é 1, consideramos o coeficiente de x.
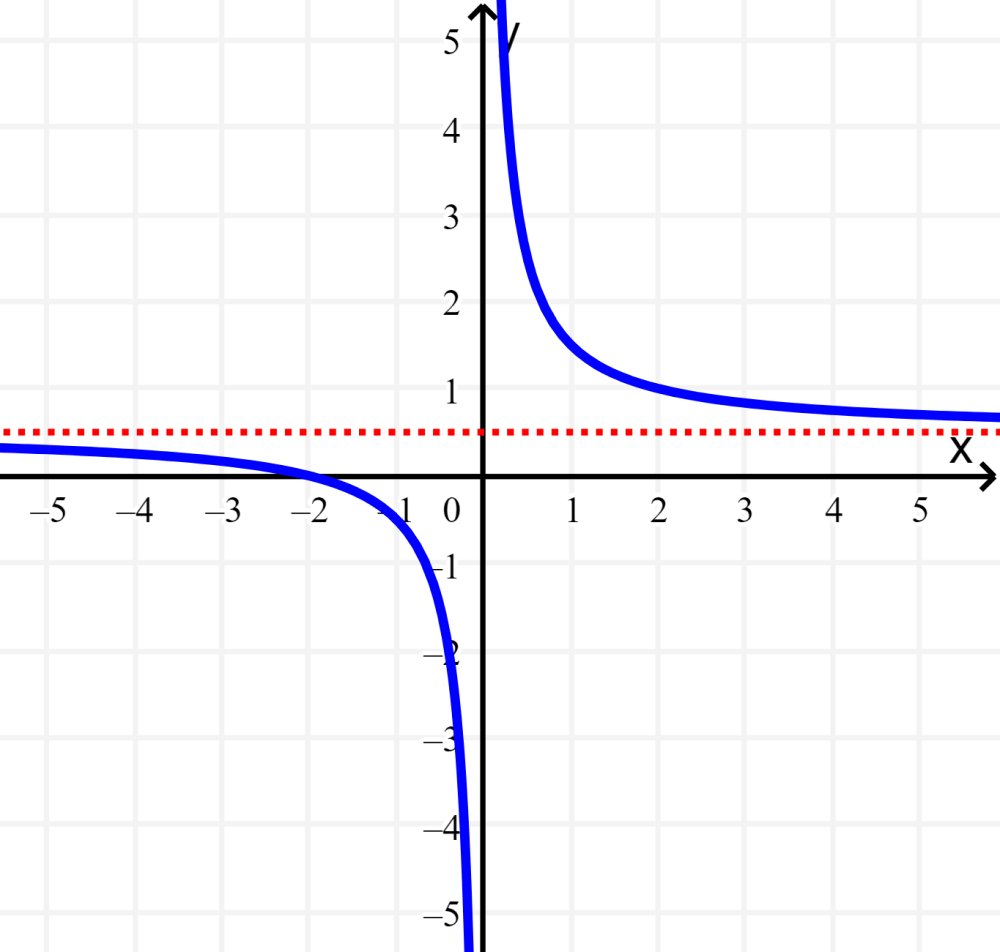
Neste caso, a assíntota horizontal está localizada em $latex y=\frac{1}{2}$:
EXEMPLO 2
Encontre as assíntotas horizontais da função $latex g(x)=\frac{x}{{{x}^2}+2}$.
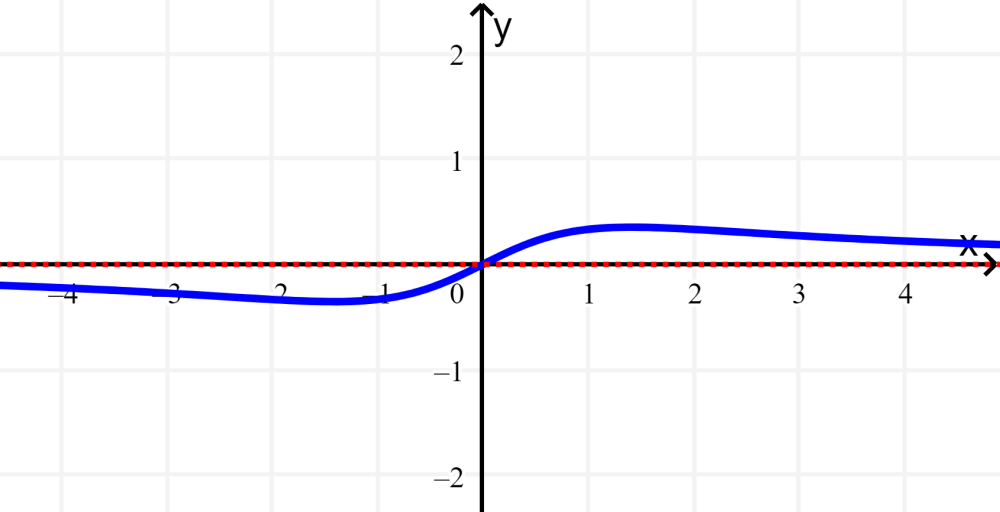
Solução: Aqui podemos ver que o grau do numerador é menor que o grau do denominador, portanto, a assíntota horizontal está localizada em $latex y=0$:
EXEMPLO 3
Encontre as assíntotas horizontais da função $latex f(x)=\frac{{{x}^2}+2}{x+1}$.
Solução: Neste caso, o grau do numerador é maior que o grau do denominador, portanto não há assíntota horizontal:
Experimente você mesmo – Resolva os exercícios
Como calcular a assíntota oblíqua de uma função?
Para calcular a assíntota oblíqua ou inclinada de uma função, devemos comparar o grau do numerador e o grau do denominador. Se o grau do numerador for exatamente um a mais do que o grau do denominador, o gráfico da função racional será aproximadamente uma linha inclinada com algumas partes complicadas no meio. A assíntota desse tipo de função é chamada de assíntota oblíqua ou inclinada.
Podemos obter a equação dessa assíntota realizando uma longa divisão de polinômios. A equação da assíntota é a parte inteira do resultado da divisão.
EXEMPLO
Encontre a assíntota oblíqua da função $latex f(x)=\frac{-3{{x}^2}+2}{x-1}$.
Solução: Começamos fazendo a longa divisão desta expressão racional:
No topo temos o quociente, a expressão linear $latex -3x-3$. Na parte inferior, temos o restante. Isso significa que, por meio da divisão, convertemos a função em uma expressão mista:
$latex f(x)=-3x-3+\frac{-1}{x-1}$
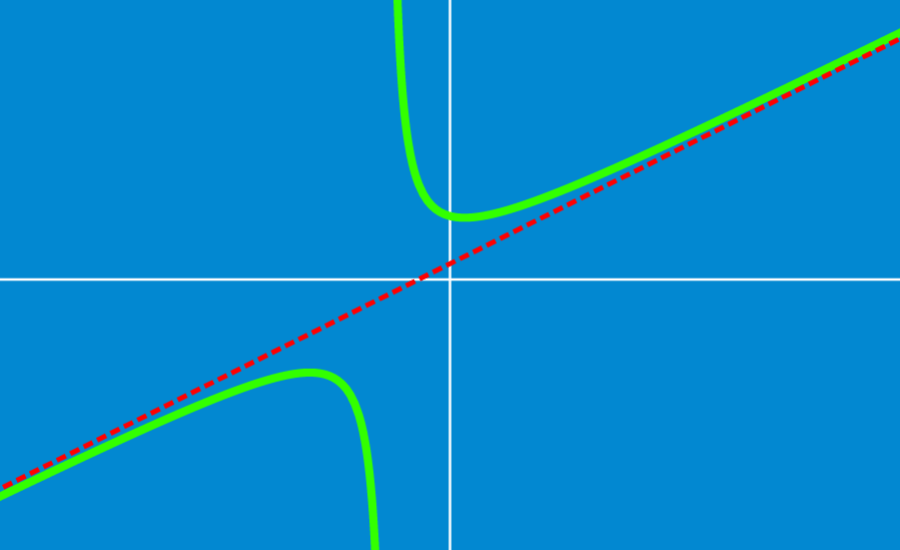
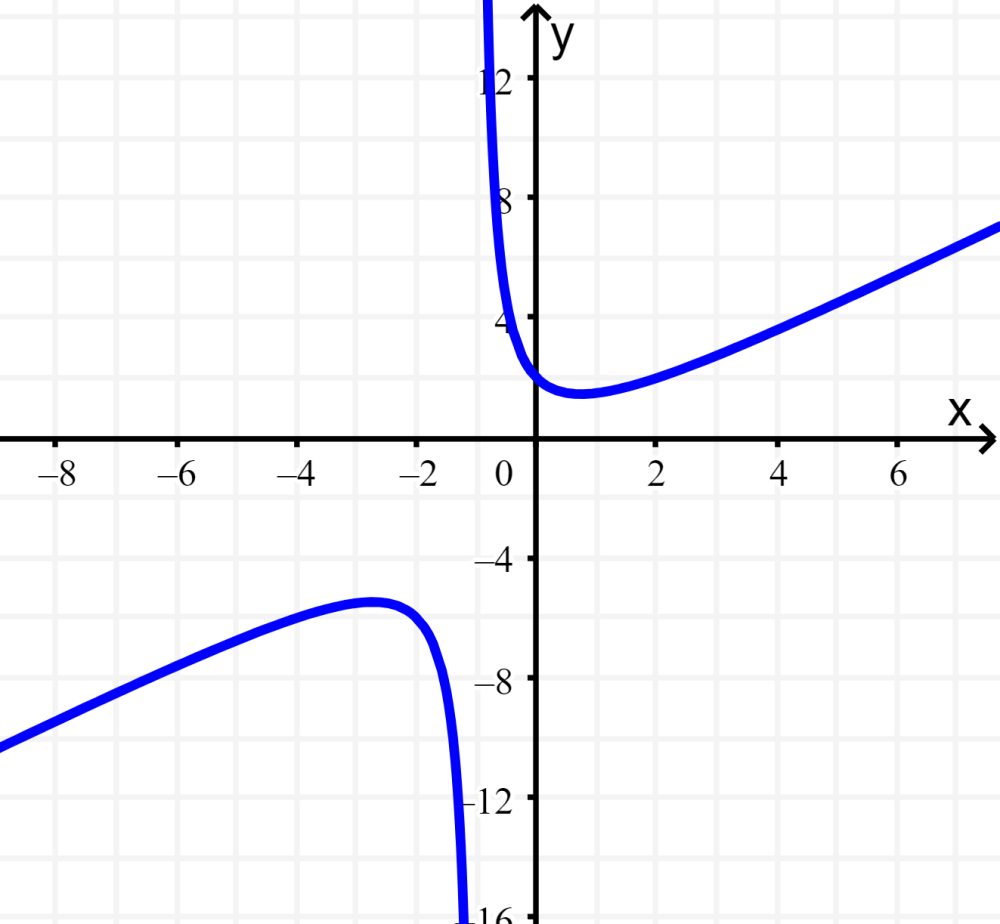
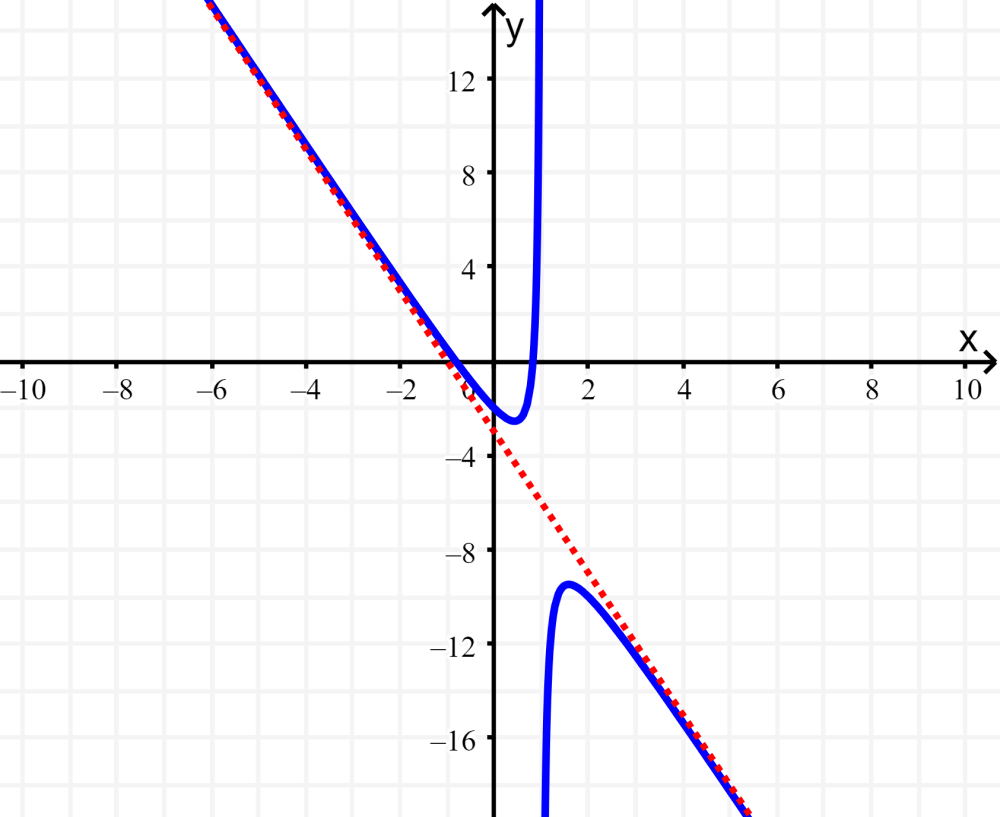
Esta é a mesma função, nós apenas a reorganizamos. Representando graficamente a função junto com a linha $latex y=-3x-3$, podemos ver que esta linha é a assíntota oblíqua da função:
Experimente você mesmo – Resolva os exercícios
Veja também
Você quer aprender mais sobre funções? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
