O gráfico do seno caracteriza-se por ser uma função que possui um período de 2π. Isso significa que a função se repete a cada 2π e se estende indefinidamente nas direções positiva e negativa. Portanto, o domínio da função é igual a todos os números reais, pois os valores de x podem assumir qualquer valor.
No entanto, a imagem de uma função seno básica é de -1 a 1, então os valores de y são de -1 a 1. Podemos obter mais variações do gráfico seno se alterarmos seus diferentes parâmetros, como amplitude, fase, período e sua translação vertical.
TRIGONOMETRIA
Relevante para…
Aprender a representar graficamente a função seno com exercícios.
TRIGONOMETRIA
Relevante para…
Aprender a representar graficamente a função seno com exercícios.
Gráfico da função seno básica
No gráfico da função seno, traçamos os ângulos no eixo x e traçamos o resultado do seno de cada ângulo no eixo y. O gráfico do seno é uma curva que varia de -1 a 1 e se repete a cada 2π. Esses tipos de curvas são chamadas de senoidais.
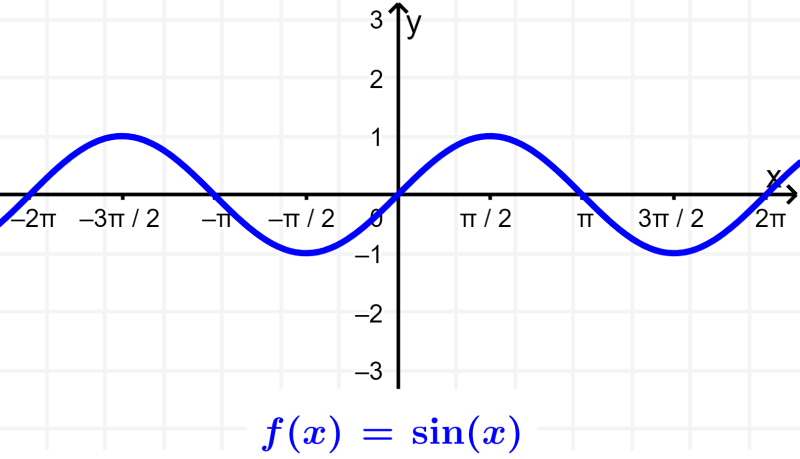
Claramente, podemos ver que a função se repete em intervalos regulares de 2π. Além disso, notamos também que o gráfico é simétrico em relação à origem, ou seja, simétrico em 180°. Isso significa que a função seno é uma função ímpar.
Domínio da função seno
A função seno se estende indefinidamente tanto para o lado x positivo quanto para o lado x negativo. Esta função faz um loop indefinidamente com um período de 2π ou 360°, então podemos usar qualquer ângulo como entrada.
Portanto, o domínio da função seno é igual a todos os números reais.
Imagem de função seno
O gráfico da função seno básica nos mostra que os valores de y variam de -1 a 1. A função sempre retorna valores dentro desse intervalo e nunca sai de esses valores. Isso significa que a imagem da função seno é todos os números reais entre 1 e -1.
Gráficos de variações da função seno
Podemos obter variações da função seno básica modificando vários parâmetros na forma geral do seno. A forma geral da função seno é:
$latex y=A~\sin(Bx-C)+D$
Modificando os parâmetros desta função, podemos obter diferentes variações do gráfico senoidal. Cada parâmetro afeta diferentes características do gráfico.
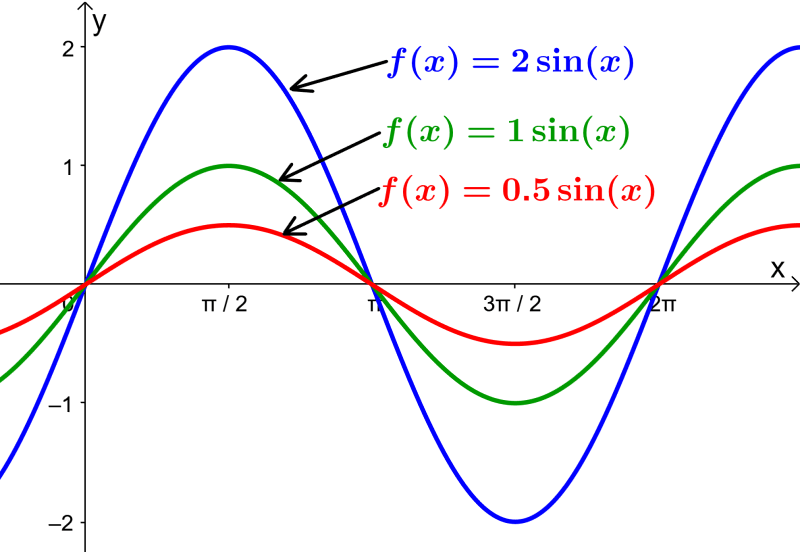
Variar a amplitude da função seno
A amplitude da função seno representa a distância da linha média do gráfico ao ponto mais alto ou mais baixo. A amplitude é medida em valor absoluto.
Também podemos pensar na amplitude como uma medida da altura do gráfico. A função seno básica tem uma amplitude de 1 e sua linha média está localizada no eixo x.
Usando a forma geral do seno, sua amplitude é encontrada usando |A|. Por exemplo, a largura de $latex y=4\sin(x)$ é 4.
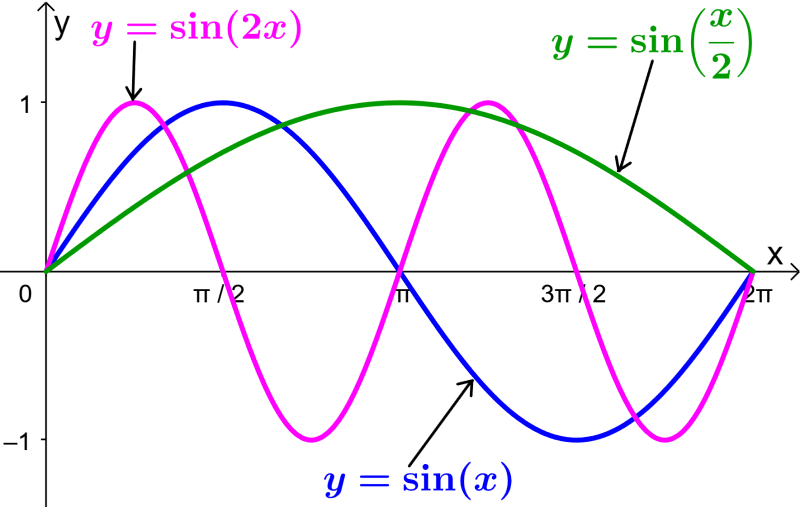
Variar o período da função seno
O período da função seno é o intervalo após o qual a função se repete. O período da função seno básica é 2π.
O período é afetado pelo parâmetro B de maneira geral. Para encontrar o período nesta forma usamos a equação $latex P=\frac{2\pi}{|B|}$. Quando temos B>1, a função “se move” mais rápido e o período é menor que 2π.
Isso faz com que a função seja compactada horizontalmente. Quando temos B<1, a função “se move” mais lentamente e o período é maior que 2π. Isso resulta na função sendo esticada horizontalmente.
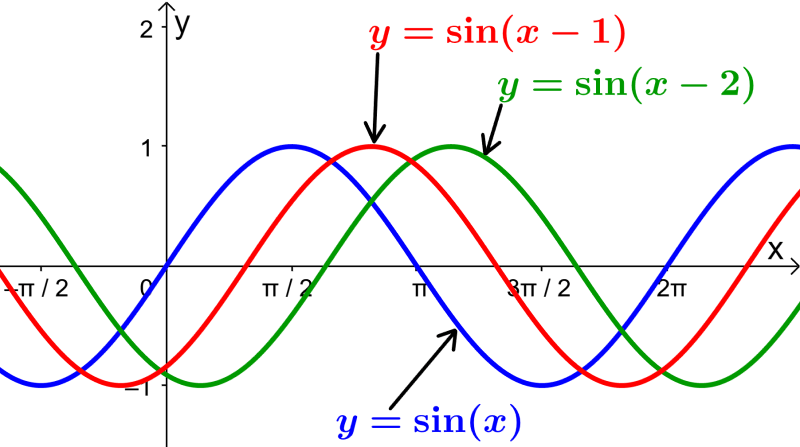
Variar a fase da função seno
A fase da função seno é a translação horizontal da função em relação à função seno básica.
Podemos encontrar a fase reescrevendo a forma geral da função da seguinte forma: $latex y=A~\sin(B(x-\frac{C}{B})+D$. Usando esta forma, a fase é igual para $latex \frac{C}{B}$.
Quando temos C>0, o gráfico tem um deslocamento para a direita. Quando temos C<0, o gráfico tem um deslocamento para a esquerda.
Variar a translação vertical da função seno
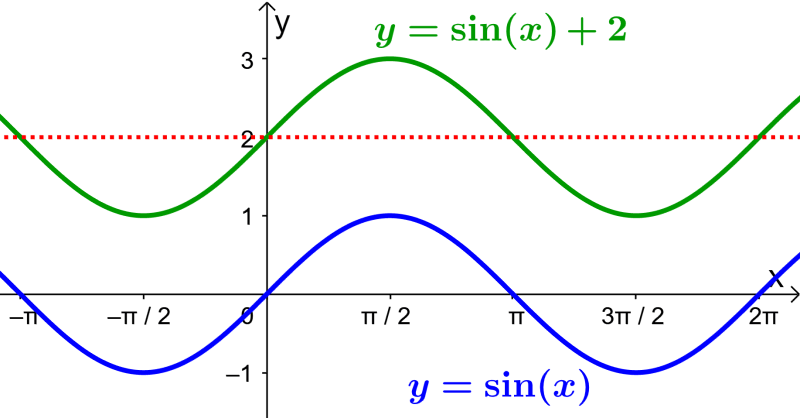
A translação ou deslocamento vertical corresponde ao valor de D na forma geral da função seno. O valor de D é o deslocamento vertical da linha do meio do gráfico.
Quando D é positivo, o gráfico é deslocado para cima. Quando D é negativo, o gráfico é deslocado para baixo. Por exemplo, a função $latex y=\sin(x)+D$ tem sua linha do meio em $latex y=D$.
Exercícios de gráfico de seno resolvidos
O que você aprendeu sobre gráficos de seno é aplicado para resolver os seguintes exercícios práticos. Tente resolver os exercícios antes de olhar para a resposta.
EXERCÍCIO 1
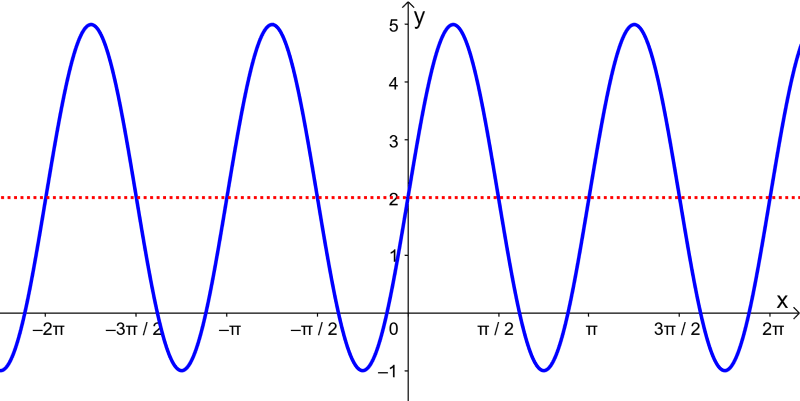
Se tivermos a função $latex y=3\sin(2x)+2$, qual é o seu gráfico?
Solução
Temos que encontrar as características que a função terá usando seus diferentes parâmetros. Comparando esta função com a forma geral do seno, vemos que:
- Amplitude: $latex |A|=3$. O gráfico será três vezes mais alto.
- Período: $latex P=\frac{2\pi}{|B|}=\frac{2\pi}{2}=\pi$. O período é dividido pela metade, então o gráfico será comprimido horizontalmente.
- Fase: $latex \frac{C}{B}=0$. A função não tem fase.
- Translação vertical: $latex D=2$. Temos a linha do meio em $latex y=2$.
Assim, determinamos que o gráfico da função é:
EXERCÍCIO 2
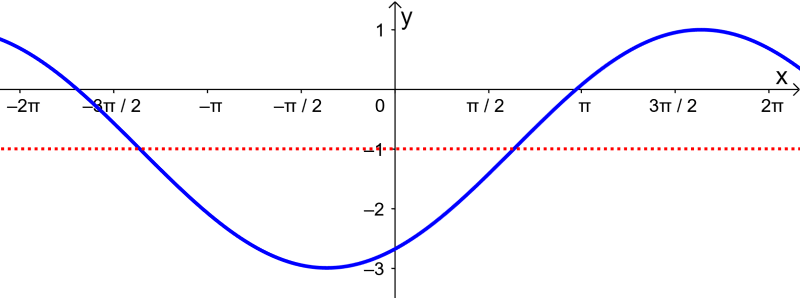
Qual é o gráfico da função $latex y=2\sin(\frac{1}{2}x-1)-1$?
Solução
Comparamos a função em sua forma geral com a função dada para extrair as seguintes informações:
- Amplitude: $latex |A|=2$. O gráfico será duas vezes mais alto.
- Período: $latex P=\frac{2\pi}{|B|}=\frac{2\pi}{\frac{1}{2}}=4\pi$. O período é o dobro da função básica, então o gráfico será esticado horizontalmente.
- Fase: $latex \frac{C}{B}=\frac{1}{\frac{1}{2}}=2$. O gráfico é deslocado 2 unidades para a direita.
- Translação vertical: $latex D=-1$. Sua linha média está em $latex y=-1$.
Aplicando essas transformações à função seno básica, temos:
EXERCÍCIO 3
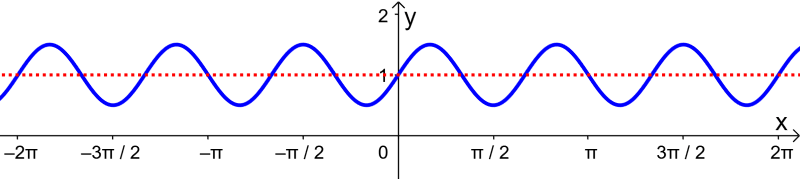
Qual é a equação da seguinte função seno?
Solução
Observando o gráfico, podemos obter as seguintes informações:
- A distância da linha média ao ponto mais alto é 0,5. Isso significa que $latex A=\frac{1}{2}$.
- O gráfico tem um período de $latex \frac{2\pi}{3}$. Então, temos que o parâmetro B deve ser 3.
- O gráfico não tem deslocamento horizontal, então C deve ser 0.
- A linha do meio está localizada em $latex y=1$, então D é igual a 1.
Com essas informações, concluímos que a equação desta função é:
$latex y=\frac{1}{2}\sin(3x)+1$
EXERCÍCIO 4
Qual é a equação da seguinte função seno?
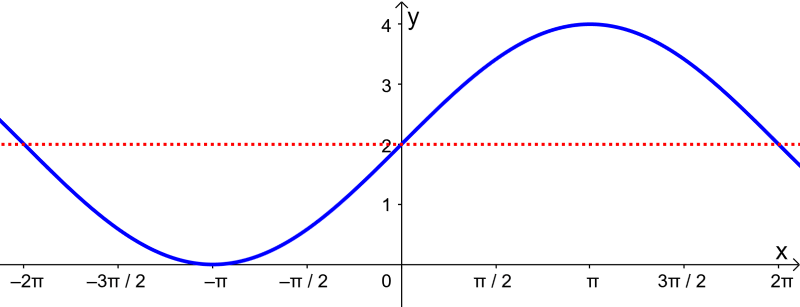
Solução
Extraímos as seguintes informações do gráfico da função:
- A altura é duas vezes a função seno básica, então $latex A=2$.
- O período da função é 4π, então temos $latex B=\frac{1}{2}$.
- Não temos nenhum deslocamento horizontal, então C deve ser 0.
- A linha do meio está localizada em $latex y=2$, então D é igual a 2.
Usando essas informações, concluímos que a equação do gráfico é:
$latex y=2\sin(\frac{1}{2}x)+2$
Veja também
Interessado em aprender mais sobre a função seno? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
