Os sistemas de coordenadas podem ser definidos como formas de localizar pontos no espaço. No espaço tridimensional, o sistema de coordenadas cartesianas tem a forma (x, y, z). No entanto, este sistema nem sempre é o mais conveniente, por isso temos sistemas de coordenadas alternativos. Um desses sistemas é o sistema de coordenadas cilíndricas.
As coordenadas cilíndricas são consideradas como uma extensão das coordenadas polares na terceira dimensão. A forma geral de coordenadas cilíndricas é (r, θ, z), onde r é a distância da origem ao ponto no plano xy, θ é o ângulo em relação ao eixo x, e z é o mesmo componente z do que em coordenadas cartesianas.
O que são coordenadas cilíndricas?
As coordenadas cilíndricas são definidas como um sistema de coordenadas tridimensional alternativo ao sistema cartesiano. As coordenadas cilíndricas são escritas na forma (r, θ, z), onde r representa a distância da origem ao ponto no plano xy, θ representa o ângulo formado em relação ao eixo x e z é o componente z, que é o mesmo que em coordenadas cartesianas.
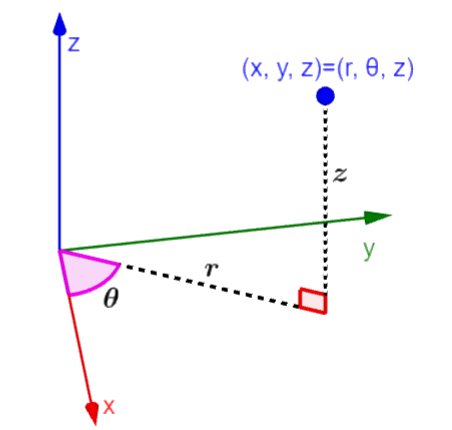
Este sistema de coordenadas é usado principalmente para representar graficamente formas cilíndricas, como tubos ou tanques. Isso é principalmente conveniente no cálculo, pois dependendo das equações dadas, encontrar suas derivadas ou integrais pode ser mais fácil.
Exemplos de Coordenadas Cilíndricas
Para localizar um ponto em coordenadas cilíndricas, começamos localizando-o no plano xy medindo a distância da origem e medindo o ângulo do eixo x. Em seguida, adicionamos o componente z. No gráfico abaixo, podemos observar o ponto $latex (3, \frac{\pi}{3}, 4)$.
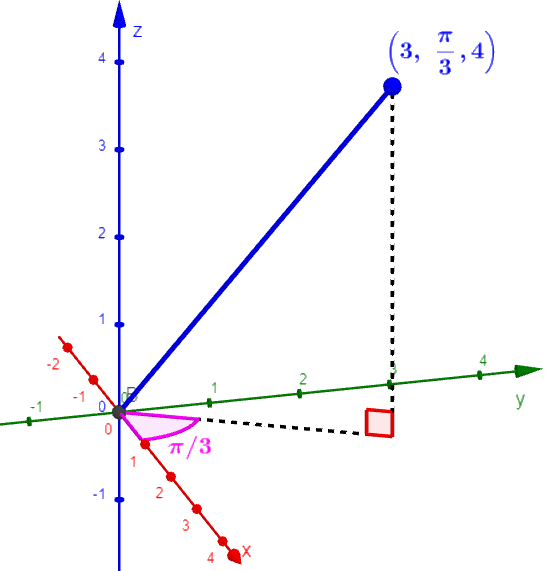
Uma característica das coordenadas cilíndricas é que podemos descrever um ponto usando várias coordenadas. Ou seja, há um número infinito de coordenadas para cada ponto. Isso ocorre porque o ângulo θ pode ser escrito de diferentes maneiras.
Se somarmos ou subtrairmos 2π, obtemos um ângulo equivalente. Por exemplo, os ângulos $latex \frac{\pi}{2}$, $latex \frac{5\pi}{2}$ e $latex -\frac{3\pi}{2}$ são os mesmos.
Fórmulas de conversão de coordenadas cilíndricas para cartesianas
Usamos o diagrama a seguir para derivar as fórmulas de conversão de coordenadas cilíndricas para coordenadas cartesianas:
Podemos ver que a coordenada z é a mesma em ambos os sistemas. Então, só precisamos encontrar os valores de x e y em termos de r e θ. Podemos usar a função cosseno para encontrar o componente x e a função seno para encontrar o componente y. Então temos:
| $latex x=r~\cos(\theta)$ $latex y=r~\sin(\theta)$ $latex z=z$ |
EXERCÍCIO 1
Se tivermos as coordenadas cilíndricas $latex (3, \frac{\pi}{4}, 4)$, qual é o seu equivalente em coordenadas cartesianas?
Solução
Podemos reconhecer os valores $latex r=3, ~\theta=\frac{\pi}{4}$. Usamos as fórmulas vistas acima com estes valores:
$latex x=3 \cos(\frac{\pi}{4})$
$latex x=2,1$
$latex y=3 \sin(\frac{\pi}{4})$
$latex y=2,1$
As coordenadas cartesianas são (2,1, 2,1, 4).
EXERCÍCIO 2
Temos as coordenadas cilíndricas $latex (10, \frac{7\pi}{4}, 5)$. Qual é o seu equivalente em coordenadas cartesianas?
Solução
Temos os valores $latex r=10, ~\theta=\frac{7\pi}{4}$. Usando esses valores, encontramos os valores de x e y:
$latex x=10 \cos(\frac{7\pi}{4})$
$latex x=7,07$
$latex y=10 \sin(\frac{7\pi}{4})$
$latex y=-7,07$
As coordenadas cartesianas são (7,07, -7,07, 5).
Fórmulas de conversão de coordenadas cartesianas para cilíndricas
Para derivar as fórmulas de conversão de coordenadas cartesianas para cilíndricas, usaremos o mesmo diagrama:
O valor de r é encontrado usando o teorema de Pitágoras com as componentes x e y. Então temos:
$latex {{r}^2}={{x}^2}+{{y}^2}$
| $latex r=\sqrt{{{x}^2}+{{y}^2}}$ |
O ângulo θ pode ser encontrado usando a tangente inversa. Sabemos que a tangente é igual ao lado oposto dividido pelo lado adjacente. No diagrama, vemos que o lado oposto é y e o lado adjacente é x. Então temos:
| $latex \theta=\tan^{-1}(\frac{y}{x})$ |
Algo que temos que considerar com esse ângulo é que às vezes o valor dado pela calculadora está errado. Isso ocorre porque as saídas da tangente inversa vão de $latex -\frac{\pi}{2}$ para $latex \frac{\pi}{2}$ e isso não cobre todos os quatro quadrantes.
Podemos corrigir isso adicionando 180° ou π quando o ponto estiver no segundo e terceiro quadrantes e adicionando 360° ou 2π quando o ponto estiver no quarto quadrante. Quando o ponto está no primeiro quadrante, o valor dado pela calculadora é correto.
EXERCÍCIO 1
O ponto (4, 6, 7) está em coordenadas cartesianas. Qual é o seu equivalente em coordenadas cilíndricas?
Solução
Temos os valores $latex x=4,~y=6$. Podemos encontrar r e θ usando as fórmulas dadas acima. Assim, o valor de r é:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{4}^2}+{{6}^2}}$
$latex r=\sqrt{16+36}$
$latex r=\sqrt{52}$
$latex r=7,2$
O ângulo θ é:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{6}{4})$
$latex \theta=0,98$ rad
Tanto a componente x quanto a componente y são positivas, então o ponto está no primeiro quadrante e o ângulo obtido está correto.
As coordenadas do ponto são (7,2, 0,98 rad, 7).
EXERCÍCIO 2
Temos o ponto (-3, -6, 5) em coordenadas cartesianas. Qual é a sua equivalência em coordenadas cilíndricas?
Solução
Reconhecemos $latex x=-3,~y=-6$. Usamos as fórmulas acima para encontrar r e θ:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{(-3)}^2}+{{(-6)}^2}}$
$latex r=\sqrt{9+36}$
$latex r=\sqrt{47}$
$latex r=6,9$
O ângulo θ é:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{-6}{-3})$
$latex \theta=1,11$ rad
Tanto o componente x quanto o componente y são negativos, então o ponto está no terceiro quadrante e precisamos adicionar π para obter o ângulo correto. Então o ângulo correto é $latex \theta=1,11+\pi=4,25$ rad.
As coordenadas do ponto são (6,9, 4,25 rad, 5).
Veja também
Interessado em aprender mais sobre coordenadas cilíndricas e outros sistemas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
