Coordenadas cilíndricas são um sistema de coordenadas tridimensional alternativo ao sistema de coordenadas cartesianas. As coordenadas cilíndricas têm a forma (r, θ, z), onde r é a distância no plano xy, θ é o ângulo de r em relação ao eixo x e z é o componente do eixo z. Este sistema de coordenadas pode ter vantagens sobre o sistema cartesiano ao desenhar figuras cilíndricas como tubos ou tanques.
A seguir, conheceremos as fórmulas que podemos usar para transformar de coordenadas cartesianas em coordenadas cilíndricas. Em seguida, veremos alguns exercícios práticos nos quais aplicaremos essas fórmulas.
TRIGONOMETRIA
Relevante para…
Aprender a transformar de coordenadas cartesianas para cilíndricas.
TRIGONOMETRIA
Relevante para…
Aprender a transformar de coordenadas cartesianas para cilíndricas.
Como transformar de coordenadas cartesianas para coordenadas cilíndricas?
Coordenadas cilíndricas podem ser mais convenientes quando queremos representar graficamente cilindros, tubos ou figuras semelhantes. Este sistema de coordenadas é usado em cálculo, pois permite um sistema referencial mais fácil de ser usado para figuras cilíndricas e encontrar derivadas ou integrais é mais fácil.
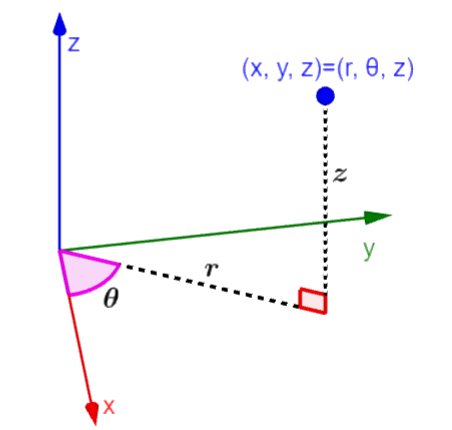
O sistema de coordenadas cilíndricas tem a forma $latex (r, ~\theta, ~z)$, onde r é a distância da origem até a localização do ponto no plano xy e θ é o ângulo formado pela linha e o eixo x.
Este sistema de coordenadas é considerado como uma extensão para a terceira dimensão do sistema de coordenadas polares. Comparando essas coordenadas com as coordenadas cartesianas, $latex (x,~y,~z)$, vemos que a componente da terceira dimensão, z, é a mesma.
Podemos usar um triângulo retângulo e o teorema de Pitágoras para encontrar o valor de r em termos de x e y. As coordenadas x e y formam os catetos do triângulo e r forma a hipotenusa. Então, temos a relação:
$latex {{r}^2}={{x}^2}+{{y}^2}$
| $latex r=\sqrt{{{x}^2}+{{y}^2}}$ |
Para encontrar o ângulo θ, usamos a função tangente inversa. A função tangente de um ângulo em um triângulo é igual ao lado oposto dividido pelo lado adjacente. Neste caso, o lado oposto é igual à coordenada y e o lado adjacente é a coordenada x. Então temos:
| $latex \theta=\tan^{-1}(\frac{y}{x})$ |
Uma complicação ao encontrar o ângulo θ é que, muitas vezes, a calculadora não retorna o valor correto do ângulo. Isso ocorre porque o intervalo da função tangente inversa é de $latex -\frac{\pi}{2}$ a $latex \frac{\pi}{2}$ e isso não cobre todos os quatro quadrantes do plano cartesiano.
Podemos resolver isso usando a tabela a seguir para corrigir os ângulos:
| Quadrante | Valor de $latex {{\tan}^{-1}}$ |
| I | A calculadora dá o valor correto |
| II | Devemos adicionar 180° ao valor da calculadora |
| III | Devemos adicionar 180° ao valor da calculadora |
| IV | Devemos adicionar 360° ao valor da calculadora |
Exercícios resolvidos de coordenadas cartesianas para cilíndricas
As fórmulas de transformação de coordenadas cartesianas para cilíndricas são aplicadas para resolver os exercícios a seguir. Tente resolver os exercícios antes de olhar para a resposta.
EXERCÍCIO 1
Se tivermos as coordenadas cartesianas (2, 2, 5), qual é a equivalência em coordenadas cilíndricas?
Solução
Sabemos que temos $latex x=2,~y=2,~z=5$. Então, temos que encontrar r, θ e z para formar as coordenadas cilíndricas. Encontramos r, usando a seguinte equação:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{2}^2}+{{2}^2}}$
$latex r=\sqrt{4+4}$
$latex r=\sqrt{8}$
Encontramos θ, usando a seguinte fórmula:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{2}{2})$
$latex \theta={{\tan}^{-1}}(1)$
$latex \theta=45$° $latex =\frac{\pi}{4}$
O componente z é o mesmo, então as coordenadas cilíndricas são $latex (\sqrt{8},~ \frac{\pi}{4}, ~5)$.
EXERCÍCIO 2
O ponto (-3, 6, 3) está em coordenadas cartesianas. Qual é o seu equivalente em coordenadas cilíndricas?
Solução
Temos os valores $latex x=-3,~y=6,~z=3$. Temos que encontrar r, θ e z, usando esses valores. Começamos com r:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{(-3)}^2}+{{6}^2}}$
$latex r=\sqrt{9+36}$
$latex r=\sqrt{45}$
$latex r=3\sqrt{5}$
Agora, encontramos o ângulo θ, usando a seguinte fórmula:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{6}{-3})$
$latex \theta={{\tan}^{-1}}(-2)$
$latex \theta=-63,4$°
No entanto, vemos que o ponto está localizado no segundo quadrante, pois o componente x é negativo e o componente y é positivo. Então, temos que adicionar 180° ao valor obtido. Isso significa que o ângulo é $latex \theta=-63,4+180=116,6$°.
A componente em z é a mesma. Portanto, o ponto em coordenadas cilíndricas é $latex (3\sqrt{5}, ~116,6^{\circ}, ~3)$.
EXERCÍCIO 3
Se tivermos o ponto (-4, -1, -3) em coordenadas cartesianas, qual a sua equivalência em coordenadas cilíndricas?
Solução
Podemos reconhecer os valores $latex x=-4,~y=-1,~z=-3$. Para encontrar esse ponto em coordenadas cilíndricas, precisamos encontrar r, θ e z. Podemos encontrar r, usando a seguinte equação:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{(-4)}^2}+{{(-1)}^2}}$
$latex r=\sqrt{16+1}$
$latex r=\sqrt{17}$
Agora, encontramos o ângulo θ, usando a seguinte fórmula:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{-1}{-4})$
$latex \theta=14$°
Nesse caso, o ponto está no terceiro quadrante, pois tanto o componente x quanto o componente y são negativos. Então, temos que adicionar 180° ao ângulo obtido para encontrar o ângulo correto. O ângulo correto é $latex \theta=14+180=194$°.
Como o componente z é o mesmo, as coordenadas cilíndricas são $latex (\sqrt{17}, ~194^{\circ}, ~-3)$.
EXERCÍCIO 4
Determine a equivalência em coordenadas cilíndricas do ponto (2, -6, 4).
Solução
Reconhecemos os valores $latex x=2,~y=-6,~z=4$. Usamos esses valores para encontrar r, θ e z e formar as coordenadas cilíndricas. Encontramos r usando a seguinte equação:
$latex r=\sqrt{{{x}^2}+{{y}^2}}$
$latex r=\sqrt{{{2}^2}+{{(-6)}^2}}$
$latex r=\sqrt{4+36}$
$latex r=\sqrt{40}$
$latex r=2\sqrt{10}$
O ângulo θ é encontrado da seguinte maneira:
$latex \theta={{\tan}^{-1}}(\frac{y}{x})$
$latex \theta={{\tan}^{-1}}(\frac{-6}{2})$
$latex \theta={{\tan}^{-1}}(-3)$
$latex \theta=-71,6$°
Notamos que o ponto está no quarto quadrante, pois o componente x é positivo e o componente y é negativo.
Portanto, temos que adicionar 360° ao ângulo dado pela calculadora para encontrar o valor correto. O ângulo correto é $latex \theta=-71,6+360=288,4$°.
Mantemos o componente z, então as coordenadas cilíndricas são $latex (2\sqrt{10}, ~288,4^{\circ}, ~4)$.
Exercícios de coordenadas cartesianas para cilíndricas para resolver
Coloque em prática o que você aprendeu sobre a transformação de coordenadas cartesianas para cilíndricas resolvendo os exercícios a seguir. Selecione uma resposta e verifique-a para certificar-se de que selecionou a correta.
Veja também
Interessado em aprender mais sobre coordenadas cilíndricas e outros sistemas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
