O vértice de uma parábola é o ponto mais alto ou mais baixo, também conhecido como máximo ou mínimo da parábola. O vértice é o ponto de intersecção da parábola e sua linha de simetria. O vértice pode ser encontrado de maneiras diferentes dependendo se a parábola está escrita na forma padrão ou na forma de vértice.
A seguir, aprenderemos sobre algumas propriedades importantes dos vértices. Então, aprenderemos como encontrar os vértices usando dois métodos. Finalmente, aplicaremos esses métodos para resolver alguns exercícios.
PRÉ-CÁLCULO
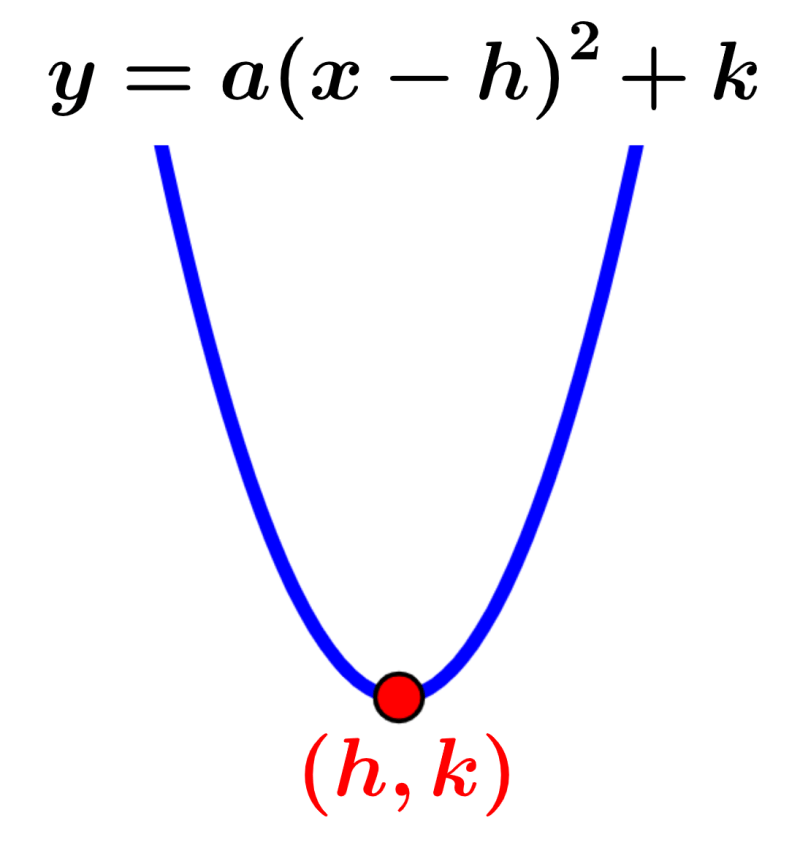
Relevante para…
Aprender a encontrar o vértice de uma parábola com exercícios.
PRÉ-CÁLCULO
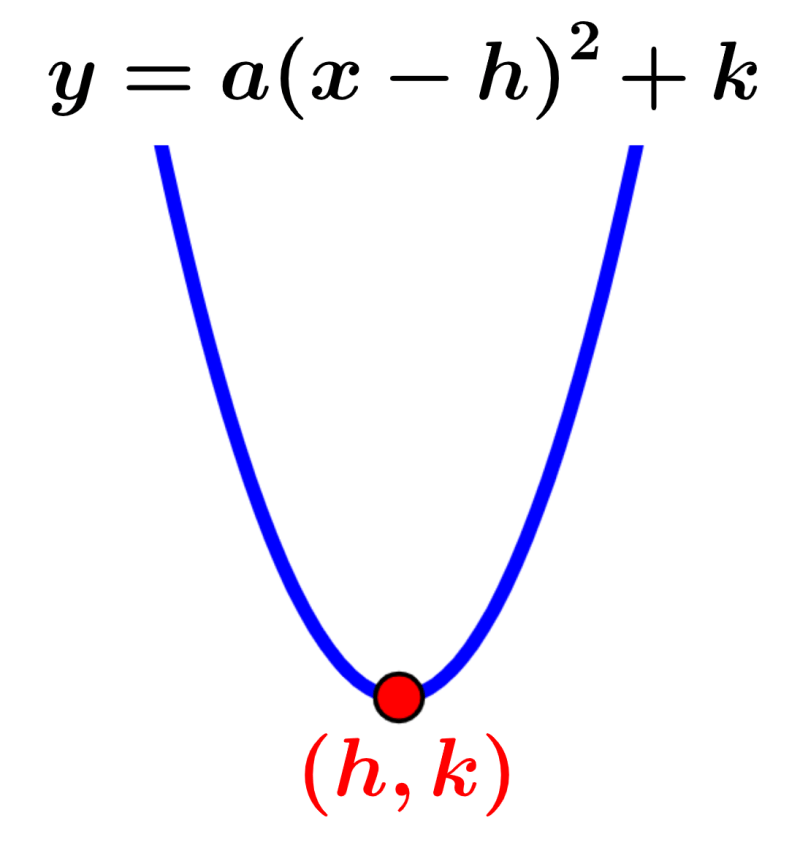
Relevante para…
Aprender a encontrar o vértice de uma parábola com exercícios.
Propriedades do vértice de uma parábola
• O vértice é o ponto máximo ou mínimo de uma parábola.
• O vértice é o ponto onde a parábola muda de direção.
• O eixo de simetria cruza o vértice.
Como encontrar o vértice de uma parábola?
O vértice de uma parábola pode ser encontrado usando a equação da parábola. As fórmulas usadas são diferentes dependendo se a equação é escrita na forma padrão ou na forma de vértice.
Encontrar o vértice usando a forma padrão
Se tivermos uma parábola escrita em sua forma padrão $latex y = a {{x}^2} + bx + c$, podemos encontrar a coordenada x do vértice usando a fórmula $latex x = – \frac{b}{2a}$. Em seguida, encontramos o valor de y substituindo o valor x do vértice na forma padrão.
Encontrar o vértice usando a forma do vértice
A forma do vértice de uma parábola nos permite encontrar o vértice facilmente. Se tivermos a equação $latex y = a {{(x-h)}^2}-k$, o vértice é $latex (h, k)$.
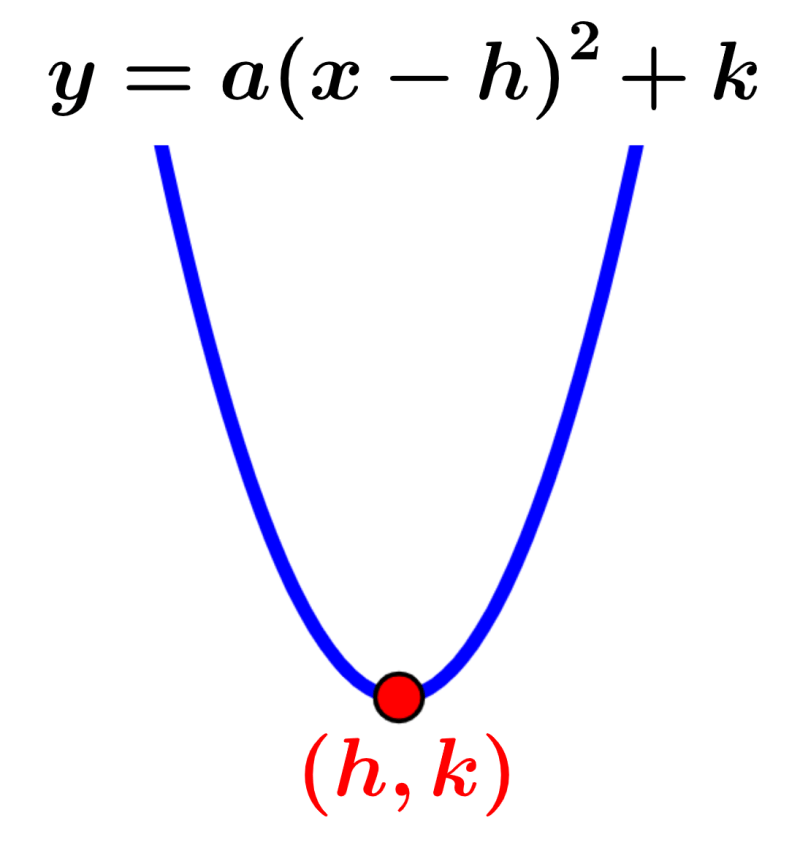
Exercícios de vértices de parábolas resolvidos
Os exercícios a seguir são usados para aplicar os métodos usados para encontrar o vértice de uma parábola. Cada exercício tem sua respectiva solução, mas é recomendável que você tente resolver os exercícios antes de olhar a resposta.
EXERCÍCIO 1
Qual é o vértice da parábola $latex y = 3 {{(x-3)}^2} +5$?
Solução
Esta parábola é escrita na forma de vértice $latex y=a{{(x-h)}^2}+k$. Desta forma, sabemos que o vértice é $latex (h, k)$. Comparando com esta equação, temos os valores:
$latex h=3$
$latex k=5$
O vértice é (3, 5).
EXERCÍCIO 2
Uma parábola é definida por $latex y = 4 {{(x + 4)}^2} -6$. Qual é o seu vértice?
Solução
Novamente, comparamos a equação dada com a forma de vértice $latex y = a {{(x-h)}^2} + k$ e obtemos os valores de h e de k :
$latex h=-4$
$latex k=-6$
O vértice é (-4, -6).
EXERCÍCIO 3
Qual é o vértice da parábola $latex y = 2 {{x}^2} + 4x + 5$?
Solução
Esta parábola foi escrita em formato padrão. Podemos obter a coordenada x do vértice usando a fórmula $latex x = – \frac{b}{2a}$. Então, temos:
$latex x=-\frac{b}{2a}$
$latex =-\frac{4}{2(2)}$
$latex =-\frac{4}{4}$
$latex =-1$
Agora, substituímos o valor de x na equação para encontrar a coordenada em y:
$latex y=2{{x}^2}+4x+5$
$latex =2{{(-1)}^2}+4(-1)+5$
$latex =2-4+5$
$latex =3$
O vértice é (-1, 3).
EXERCÍCIO 4
Se tivermos a parábola $latex y = -2 {{x}^2} + 12x-7$, qual é o seu vértice?
Solução
Usando a fórmula $latex x = – \frac{b}{2a}$, podemos encontrar a coordenada x do vértice. Então, temos:
$latex x=-\frac{b}{2a}$
$latex =-\frac{12}{2(-2)}$
$latex =-\frac{12}{-4}$
$latex =3$
Usamos este valor de x na equação para encontrar a coordenada em y:
$latex y=-2{{x}^2}+12x-7$
$latex =-2{{(3)}^2}+12(3)-7$
$latex =-18+36-7$
$latex =9$
O vértice é (3, 9).
Exercícios de vértices de parábolas para resolver
Pratique o uso dos métodos para encontrar os vértices das parábolas resolvendo os exercícios a seguir. Se precisar de ajuda com isso, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre parábolas? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
