A excentricidade da elipse é uma característica única que determina a forma da elipse. Excentricidade significa o desvio da curva que ocorreu a partir da circularidade de uma determinada figura. Portanto, uma excentricidade de 0 significa que a figura é completamente redonda e uma excentricidade menor que 1 significa que a figura é oval. A excentricidade depende da distância do centro aos focos e da distância do centro ao vértice.
A seguir, conheceremos a fórmula usada para calcular a excentricidade das elipses. Vamos resolver alguns exercícios práticos.
PRÉ-CÁLCULO
Relevante para…
Aprender sobre a excentricidade da elipse com exercícios.
PRÉ-CÁLCULO
Relevante para…
Aprender sobre a excentricidade da elipse com exercícios.
Como calcular a excentricidade das elipses?
A excentricidade das elipses é calculada usando a seguinte fórmula:
$latex e=\frac{c}{a}$
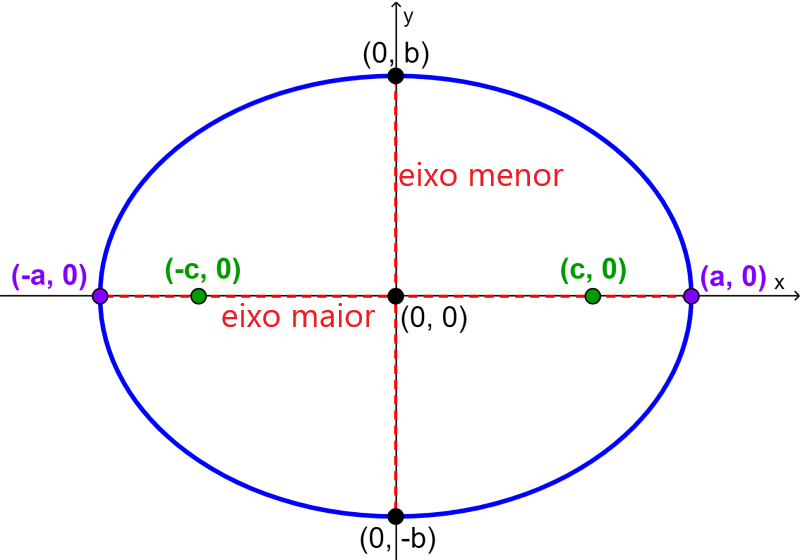
onde, c representa a distância do centro aos focos e a representa o comprimento do semieixo maior, ou seja, a distância do centro ao vértice.
Podemos calcular a distância do centro aos focos usando a fórmula:
$latex {{c}^2}={{a}^2}-{{b}^2}$
onde, a é o comprimento do semi-eixo maior e b é o comprimento do semi-eixo menor.
Sabemos que os focos da elipse estão mais próximos do centro em comparação com os vértices. Isso significa que o valor da excentricidade de uma elipse será sempre menor que 1, pois o valor do numerador será sempre menor que o valor do denominador. Quanto mais perto os focos ficam do centro, o valor da excentricidade diminui e quando os focos estão no centro, a excentricidade é igual a 0 e a figura é redonda. Ou seja, quando temos $latex e = 0$, não temos mais uma elipse, mas um círculo. Portanto, para uma elipse, temos:
$latex e=\frac{c}{a}$, en donde $latex 0<e<1$
Exercícios de excentricidade de elipse resolvidos
Os seguintes exercícios de excentricidade de elipse podem ser usados para examinar a aplicação das fórmulas vistas acima. Tente resolver os exercícios sozinho antes de ver a resposta.
EXERCÍCIO 1
Qual é a excentricidade de uma elipse que tem a equação $latex \frac{{{x}^2}}{64} + \frac{{{y}^2}}{16} = 1$?
Solução
A partir da equação, podemos identificar os seguintes valores:
$latex {{a}^2}=64$
$latex a=8$
$latex {{b}^2}=16$
$latex b=4$
Agora, usamos esses valores para encontrar c com a seguinte equação:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=64-16$
$latex {{c}^2}=48$
$latex c=6,93$
Substituímos os valores encontrados na equação de excentricidade:
$latex e=\frac{c}{a}$
$latex e=\frac{6,93}{8}$
$latex e=0,87$
EXERCÍCIO 2
Se uma elipse que possui a equação $latex \frac{{{x}^2}}{81} + \frac{{{y}^2}}{25} = 1$, qual é sua excentricidade?
Solução
Começamos identificando os valores a e b da equação fornecida:
$latex {{a}^2}=81$
$latex a=9$
$latex {{b}^2}=25$
$latex b=5$
Encontramos o valor de c usando a seguinte equação:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=81-25$
$latex {{c}^2}=56$
$latex c=7,48$
Usando a fórmula de excentricidade com os valores encontrados, temos:
$latex e=\frac{c}{a}$
$latex e=\frac{7,48}{9}$
$latex e=0,83$
EXERCÍCIO 3
Qual é a excentricidade de uma elipse que tem a equação $latex \frac{{{x}^2}}{121} + \frac{{{y}^2}}{64} = 1$?
Solução
Podemos extrair os seguintes valores da equação fornecida:
$latex {{a}^2}=121$
$latex a=11$
$latex {{b}^2}=64$
$latex b=8$
Usando esses valores, podemos encontrar c com a seguinte equação:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=121-64$
$latex {{c}^2}=57$
$latex c=7,55$
Encontramos a excentricidade usando os valores encontrados:
$latex e=\frac{c}{a}$
$latex e=\frac{7,55}{11}$
$latex e=0,69$
EXERCÍCIO 4
Temos uma elipse com a equação $latex \frac{{{x}^2}}{144} + \frac{{{y}^2}}{121} = 1$. Qual é a sua excentricidade?
Solução
Temos os seguintes valores:
$latex {{a}^2}=144$
$latex a=12$
$latex {{b}^2}=121$
$latex b=11$
Encontramos o valor de c usando esses valores na seguinte equação:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex {{c}^2}=144-121$
$latex {{c}^2}=23$
$latex c=4,8$
Usando esses dados na equação de excentricidade, temos:
$latex e=\frac{c}{a}$
$latex e=\frac{4,8}{11}$
$latex e=0,44$
Exercícios de excentricidade de elipse para resolver
Use o que você aprendeu sobre a excentricidade das elipses para resolver os exercícios a seguir. Selecione uma resposta e verifique se você obteve a resposta correta.
Veja também
Você quer aprender mais sobre elipses? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
