O heptágono é um polígono que possui sete lados e sete ângulos internos. A soma de todos os ângulos internos de um heptágono é igual a 900°. Dependendo das características que tomamos, podemos distinguir diferentes tipos de heptágonos. Por exemplo, se considerarmos o comprimento dos lados e a medida dos ângulos, podemos identificar heptágonos regulares e irregulares. Se considerarmos o contorno, podemos identificar heptágonos convexos e côncavos.
A seguir, veremos uma breve definição de heptágonos e conheceremos alguns tipos de heptágonos. Além disso, descobriremos algumas das características fundamentais dessas figuras geométricas. Finalmente, aprenderemos as fórmulas mais importantes para heptágonos regulares e as usaremos para resolver alguns exercícios.
GEOMETRIA
Relevante para…
Conhecer as características fundamentais de um heptágono.
GEOMETRIA
Relevante para…
Conhecer as características fundamentais de um heptágono.
Definição de um heptágono
Podemos definir um heptágono como um polígono com sete lados e sete ângulos internos. Por sua vez, um polígono é uma figura fechada bidimensional composta por segmentos retos.
O heptágono é formado por todos os seus lados, que se encontram de ponta a ponta. Dependendo das diferentes características, podemos distinguir os seguintes tipos de heptágonos:
- Regular e irregular
- Convexo e côncavo
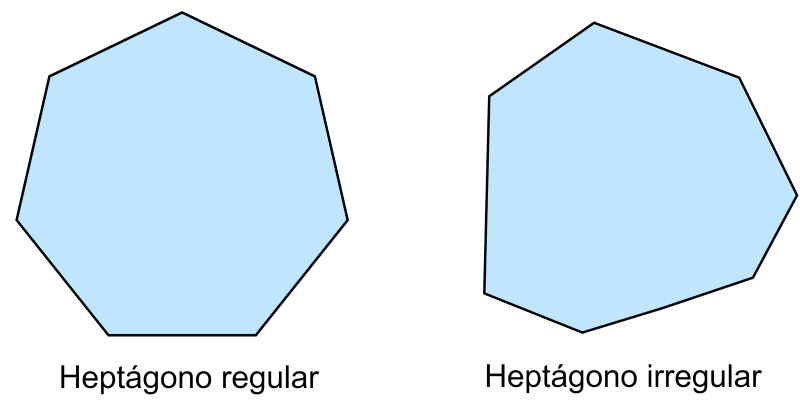
Heptágonos irregulares e regulares
Os heptágonos regulares têm a característica de ter lados com o mesmo comprimento e ângulos com a mesma medida. Os heptágonos irregulares têm a característica de ter lados de comprimentos diferentes, ângulos de medidas diferentes ou ambos ao mesmo tempo.
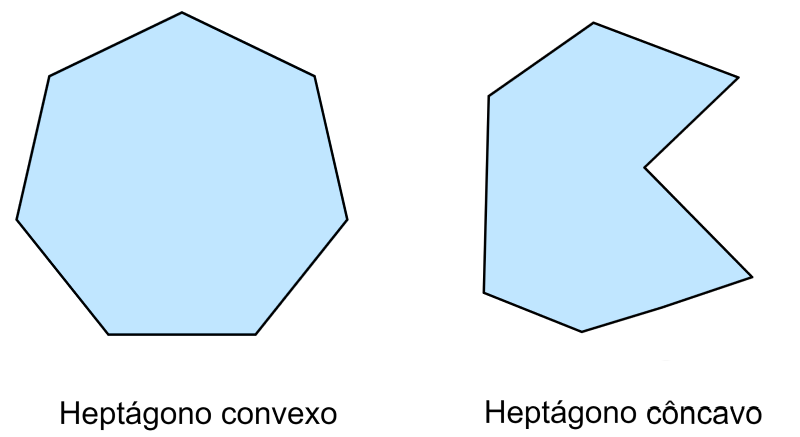
Heptágonos convexos e côncavos
Os heptágonos convexos são polígonos que têm todos os seus vértices apontando para fora. Os heptágonos côncavos são polígonos que têm pelo menos um vértice apontando para dentro.
Características fundamentais de um heptágono
Os heptágonos têm as seguintes características fundamentais:
- Em um heptágono, a soma de todos os ângulos internos é 900°.
- Um heptágono regular tem sete lados de igual comprimento.
- Um heptágono regular tem sete ângulos com a mesma medida.
- A soma total dos ângulos internos é 360°
- Cada ângulo interno de um heptágono regular mede 128,57°.
- O número total de diagonais em um heptágono regular é 14.
- O número de triângulos formados em um heptágono é sete.
Fórmulas importantes de um heptágono
As fórmulas mais importantes para um heptágono são as fórmulas de perímetro, área e apótema.
Fórmula para o perímetro de um heptágono regular
O perímetro é a soma dos comprimentos de todos os lados de um heptágono. Como um heptágono regular tem sete lados iguais, temos:
| $latex p=7l$ |
onde, l é o comprimento de um dos lados do heptágono.
Fórmula para a área de um heptágono regular
A fórmula para a área de um heptágono é:
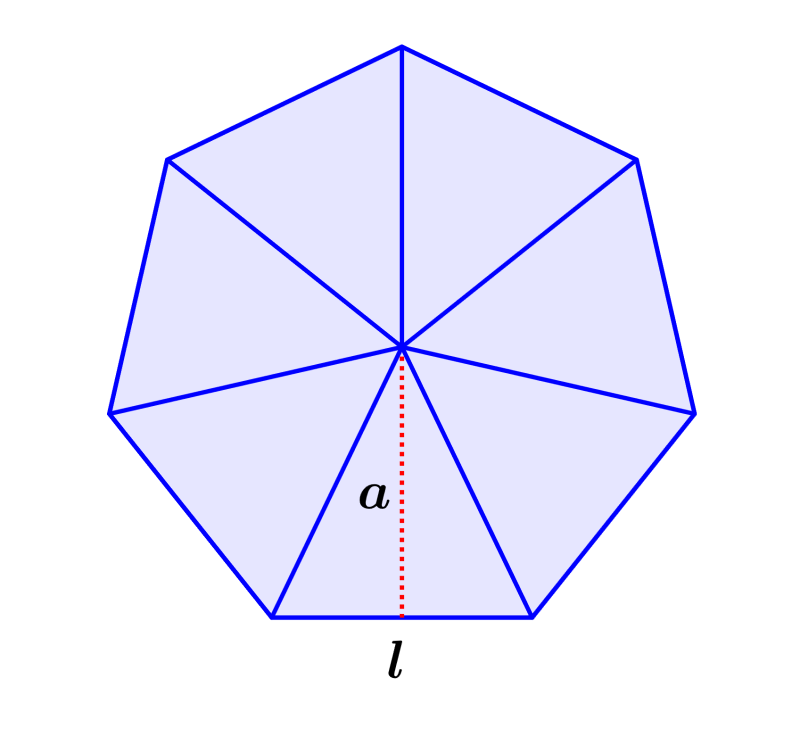
| $latex A= \frac{7}{2}la$ |
onde, l é o comprimento dos lados e a é o comprimento do apótema do heptágono.
Fórmula do apótema de um heptágono regular
Podemos encontrar o apótema de um heptágono usando a seguinte fórmula:
| $latex a= \frac{l}{2\tan(25,71°)}$ |
onde, l é o comprimento de um lado do heptágono.
Exemplos de problemas de heptágonos
EXEMPLO 1
- Qual é o perímetro de um heptágono com lados de 13 m de comprimento?
Solução: Usamos $latex l=13$ na fórmula do perímetro:
$latex p=7l$
$latex p=7(13)$
$latex p=91$
O perímetro é de 91 m.
EXEMPLO 2
- Qual é a área de um heptágono que tem lados de 11 m de comprimento e apótema de 11,42 m?
Solução: Temos $latex l=11$ e $latex a=11,42$. Então, usamos esses comprimentos na fórmula para a área:
$latex A= \frac{7}{2}la$
$latex A= \frac{7}{2}(11)(11,42)$
$latex A=439,67$
A área do heptágono é de 439,67 m².
EXEMPLO 3
- Qual é o apótema de um heptágono com lados de 10 m de comprimento?
Solução: Usamos a fórmula do apótema com $latex l=10$:
$latex a= \frac{l}{2\tan(25,71)}$
$latex a= \frac{10}{2\tan(25,71)}$
$latex a=10,38$
O comprimento do apótema é de 10,38 m.
Exercícios de heptágonos para resolver
Veja também
Você quer aprender mais sobre heptágonos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
