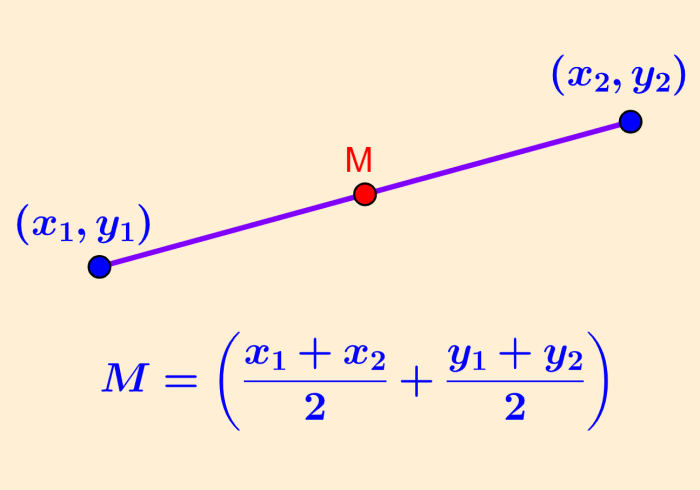
O ponto médio entre dois pontos é um ponto que tem coordenadas que se encontram exatamente no meio do caminho entre os dois pontos. Essas coordenadas podem ser encontradas somando as coordenadas x dos dois pontos e dividindo por 2. Da mesma forma, somamos as coordenadas y dos dois pontos e dividimos por 2.
A seguir, conheceremos a fórmula que podemos usar para determinar as coordenadas do ponto médio. Em seguida, usaremos essa fórmula para resolver alguns exercícios práticos.
Como determinar as coordenadas do ponto médio entre dois pontos?
Para determinar as coordenadas do ponto médio entre dois pontos, temos que usar a fórmula do ponto médio. Esta fórmula é derivada considerando que as coordenadas x do ponto médio serão iguais à soma das coordenadas x dos pontos dividida por 2 e as coordenadas y do ponto médio serão iguais à soma das coordenadas y de os pontos divididos por 2.
Então, se temos os pontos A e B com coordenadas $latex A=(x_{1}, y_{1})$ e $latex B=(x_{2}, y_{2})$, a fórmula do ponto médio é:
| Fórmula do ponto médio $latex M=\left(\frac{x_{1}+x_{2}}{2}+\frac{y_{1}+y_{2}}{2}\right)$ |
O ponto médio será expresso como as coordenadas $latex M=(x_{3}, y_{3})$.
Ponto médio entre dois pontos exercícios resolvidos
A fórmula do ponto médio é usada para determinar as coordenadas do ponto médio entre os pontos fornecidos. Tente resolver os exercícios antes de olhar para a resposta.
EXERCÍCIO 1
Determine as coordenadas do ponto médio entre os pontos (1, 4) e (5, 8).
Solução
Temos os dois pontos a seguir:
- $latex (x_{1}, y_{1})=(1, 4)$
- $latex (x_{2}, y_{2})=(5, 8)$
Aplicando a fórmula do ponto médio com os pontos dados, temos:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{1+5}{2},\frac{4+8}{2}\right)$
$latex =\left(\frac{6}{2},\frac{12}{2}\right)$
$latex =(3,~6)$
As coordenadas do ponto médio são $latex M=(3,~6)$.
EXERCÍCIO 2
Quais são as coordenadas do ponto médio entre os pontos (3, 5) e (11, 13)?
Solução
Temos as seguintes coordenadas:
- $latex (x_{1}, y_{1})=(3, 5)$
- $latex (x_{2}, y_{2})=(11, 13)$
Usamos essas coordenadas na fórmula do ponto médio e temos:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{3+11}{2},\frac{5+13}{2}\right)$
$latex =\left(\frac{14}{2},\frac{18}{2}\right)$
$latex =\left(7,~9\right)$
As coordenadas do ponto médio são $latex M=(7, 9)$.
EXERCÍCIO 3
Se tivermos os pontos (-3, -5) e (5, 8), qual é o seu ponto médio?
Solução
Podemos escrever da seguinte forma:
- $latex (x_{1}, y_{1})=(-3, -5)$
- $latex (x_{2}, y_{2})=(5, 8)$
Este exercício tem um ponto com coordenadas negativas, porém, semelhante aos exercícios anteriores, basta aplicar a fórmula do ponto médio:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{-3+5}{2},\frac{-5+8}{2}\right)$
$latex =\left(\frac{2}{2},\frac{3}{2}\right)$
$latex =\left(1,\frac{3}{2}\right)$
O ponto médio tem as coordenadas $latex M=\left(1,~\frac{3}{2}\right)$.
EXERCÍCIO 4
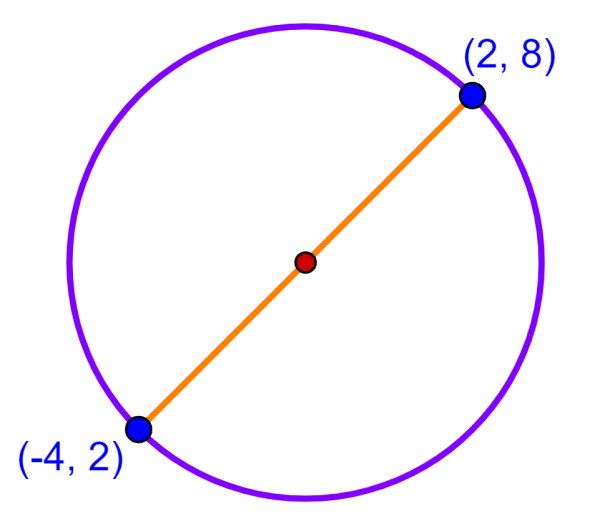
Um círculo tem um diâmetro limitado pelos pontos (-4, 2) e (2, 8). Determine as coordenadas do centro do círculo.
Solução
Lembre-se que o centro está localizado exatamente no meio do diâmetro do círculo. Assim, podemos encontrar as coordenadas do centro encontrando as coordenadas do ponto médio dos dois pontos a seguir:
- $latex (x_{1}, y_{1})=(-4,2)$
- $latex (x_{2}, y_{2})=(2,8)$
Usando a fórmula do ponto médio com essas coordenadas, temos:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{-4+2}{2},\frac{2+8}{2}\right)$
$latex =\left(\frac{-2}{2},\frac{12}{2}\right)$
$latex =(-1,~7)$
As coordenadas do centro do círculo são $latex (-1,~ 7)$.
EXERCÍCIO 5
Temos os dois pontos (m, 2) e (9, 12). Determine o valor de m se o ponto médio for (2, 7).
Solução
Temos as seguintes coordenadas:
- $latex (x_{1}, y_{1})=(m, 2)$
- $latex (x_{2}, y_{2})=(9, 12)$
- $latex (x_{3}, y_{3})=(2, 7)$
Usando a fórmula do ponto médio com as coordenadas dadas, temos:
$latex M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$
$latex =\left(\frac{m+9}{2},\frac{2+12}{2}\right)$
O valor de m faz parte das coordenadas x do ponto médio, então só temos que considerar a componente x. Então, formamos uma equação e resolvemos p. Usamos a coordenada x do ponto médio que é 2:
$latex 2=\left(\frac{m+9}{2}\right)$
$latex 4=m+9$
$latex m=-5$
O valor de m é -5.
Exercícios de ponto médio entre dois pontos para resolver
Aplique o que você aprendeu sobre o ponto médio para resolver os exercícios a seguir. Caso você precise de ajuda com isso, você pode ver os exercícios resolvidos acima.
Veja também
Interessado em aprender mais sobre ponto médio, distância e inclinação no plano? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
