A distância entre dois pontos no plano cartesiano pode ser encontrada aplicando a fórmula da distância e substituindo as coordenadas dos dois pontos dados. Por sua vez, a fórmula da distância é derivada usando o teorema de Pitágoras no plano cartesiano, onde a distância representa a hipotenusa de um triângulo retângulo.
Em seguida, revisaremos a fórmula da distância e a usaremos para resolver alguns exercícios práticos.
GEOMETRIA
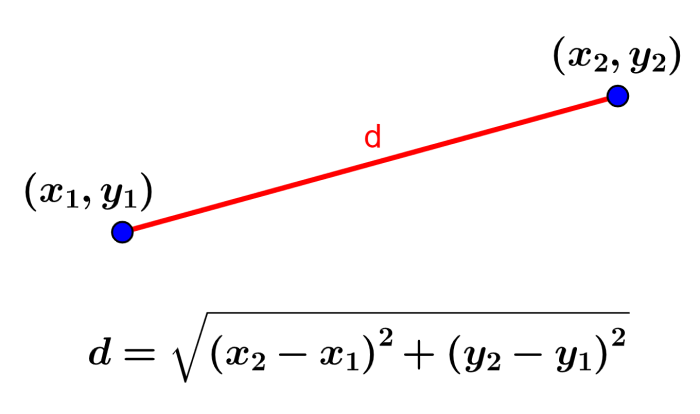
Relevante para…
Aprender a calcular a distância entre dois pontos com exercícios.
GEOMETRIA
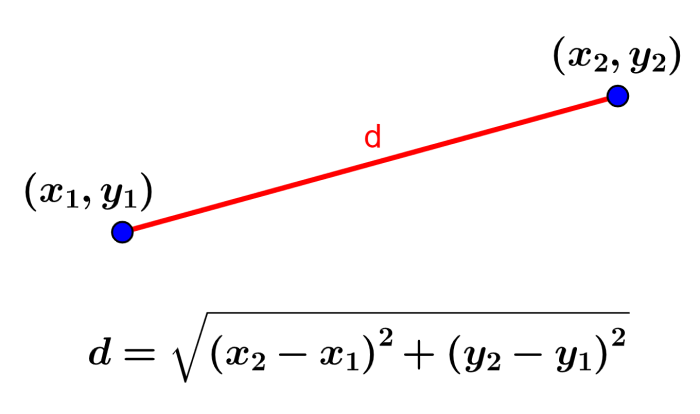
Relevante para…
Aprender a calcular a distância entre dois pontos com exercícios.
Revisão da fórmula da distância entre dois pontos
A fórmula da distância entre dois pontos é obtida quando usamos o teorema de Pitágoras no plano cartesiano, onde a hipotenusa de um triângulo retângulo representa a distância entre os pontos.
Além disso, tendo os pontos $latex A=(x_{1}, y_{1})$ e $latex B=(x_{2}, y_{2})$, a distância vertical é igual a $latex |y_ { 2}-y_{1}|$ e a distância horizontal é igual a $latex |x_{2}-x_{1}|$. Então, quando aplicamos o teorema de Pitágoras e simplificamos, temos:
| Fórmula de distância $latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$ |
Além disso, também podemos expandir a fórmula da distância para o espaço tridimensional da seguinte forma:
| Fórmula de distância 3D $$d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(z_{2}-z_{1})}^2}}$$ |
Distância entre dois pontos exercícios resolvidos
As fórmulas de distância 2D e 3D são usadas para resolver os exercícios a seguir. Tente resolver os exercícios antes de olhar para a resposta.
EXERCÍCIO 1
Determine a distância entre os pontos (3, 2) e (6, 6) no plano de coordenadas.
Solução
Escrevemos as coordenadas dadas da seguinte forma:
- $latex (x_{1}, y_{1})=(3, 2)$
- $latex (x_{2}, y_{2})=(6, 6)$
Aplicando a fórmula da distância com as coordenadas dadas, temos:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(6-3)}^2}+{{(6-2)}^2}}$
$latex =\sqrt{{{(3)}^2}+{{(4)}^2}}$
$latex =\sqrt{9+16}$
$latex =\sqrt{25}$
$latex =5$
A distância entre os dois pontos é 5.
EXERCÍCIO 2
Qual é a distância entre os pontos (-1, -3) e (5, 7)?
Solução
Temos os seguintes valores:
- $latex (x_{1}, y_{1})=(-1, -3)$
- $latex (x_{2}, y_{2})=(5, 7)$
Neste caso, temos coordenadas negativas. No entanto, a fórmula da distância se aplica independentemente dos sinais das coordenadas:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(5-(-1))}^2}+{{(7-(-3))}^2}}$
$latex =\sqrt{{{(6)}^2}+{{(10)}^2}}$
$latex =\sqrt{36+100}$
$latex =\sqrt{136}$
$latex =11,66$
A distância entre os pontos é igual a 11,66.
EXERCÍCIO 3
Se tivermos os pontos (-4, -6) e (-1, 5), qual é a sua distância?
Solução
Podemos escrever da seguinte forma:
- $latex (x_{1}, y_{1})=(-4, -6)$
- $latex (x_{2}, y_{2})=(-1, 5)$
Aplicando a fórmula da distância, temos:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(-1-(-4))}^2}+{{(5-(-6))}^2}}$
$latex =\sqrt{{{(3)}^2}+{{(11)}^2}}$
$latex =\sqrt{9+121}$
$latex =\sqrt{130}$
$latex =11,4$
A distância entre os pontos é igual a 11,4.
EXERCÍCIO 4
Temos os pontos (1, 2, 3) e (3, 4, 5) localizados no espaço tridimensional. Qual é a sua distância?
Solução
Escrevemos as coordenadas da seguinte forma:
- $latex (x_{1}, y_{1}, z_{1})=(1, 2, 3)$
- $latex (x_{2}, y_{2}, z_{2})=(3, 4, 5)$
Neste caso, os pontos dados estão no espaço tridimensional. Podemos encontrar sua distância usando a fórmula de distância 3D:
$$d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(y_{2}-y_{1})}^2}}$$
$$=\sqrt{{{(3-1)}^2}+{{(4-2)}^2}+{{(5-3)}^2}}$$
$latex =\sqrt{{{(2)}^2}+{{(2)}^2}+{{(2)}^2}}$
$latex =\sqrt{4+4+4}$
$latex =\sqrt{12}$
$latex =3,47$
A distância é igual a 3,47.
EXERCÍCIO 5
Se tivermos os pontos (-3, 4, -2) e (2, 6, 3), qual é a sua distância?
Solução
Podemos escrever da seguinte forma:
- $latex (x_{1}, y_{1}, z_{1})=(-3, 4, -2)$
- $latex (x_{2}, y_{2}, z_{2})=(2, 6, 3)$
Semelhante ao exercício anterior, temos que usar a fórmula da distância 3D com as coordenadas fornecidas. Então temos:
$$ d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(y_{2}-y_{1})}^2}}$$
$$=\sqrt{{{(2-(-3))}^2}+{{(6-4)}^2}+{{(3-(-2))}^2}}$$
$latex =\sqrt{{{(5)}^2}+{{(2)}^2}+{{(5)}^2}}$
$latex =\sqrt{25+2+25}$
$latex =\sqrt{52}$
$latex =7,21$
A distância é igual a 7,21.
Exercícios de distância entre dois pontos para resolver
Use as fórmulas de distância em 2D e 3D para resolver os exercícios a seguir. Caso você precise de ajuda com isso, você pode ver os exercícios resolvidos acima.
Veja também
Interessado em aprender mais sobre ponto médio e distância no plano? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
