O comprimento da diagonal interna de um cubo pode ser calculado usando o teorema de Pitágoras. Por meio de dois passos, podemos encontrar uma fórmula para a diagonal dos cubos. O primeiro passo exige que calculemos a diagonal de uma das faces do cubo usando os comprimentos dos lados. No segundo passo, usamos a diagonal de uma face e um dos lados para encontrar a fórmula final para a diagonal interna de um cubo.
A seguir, veremos essos passos em detalhes. Iremos derivar a fórmula para a diagonal de um cubo e usá-la para resolver alguns exercícios.
Fórmula para a diagonal do cubo
Existem duas diagonais de um cubo, a diagonal interna do cubo e a diagonal de uma face. Na imagem a seguir, podemos ver que os dois são diferentes. A diagonal interna começa em um vértice e se estende até o vértice oposto.
A diagonal de uma face começa em um vértice e termina em outro vértice, de modo que fica completamente em uma face.
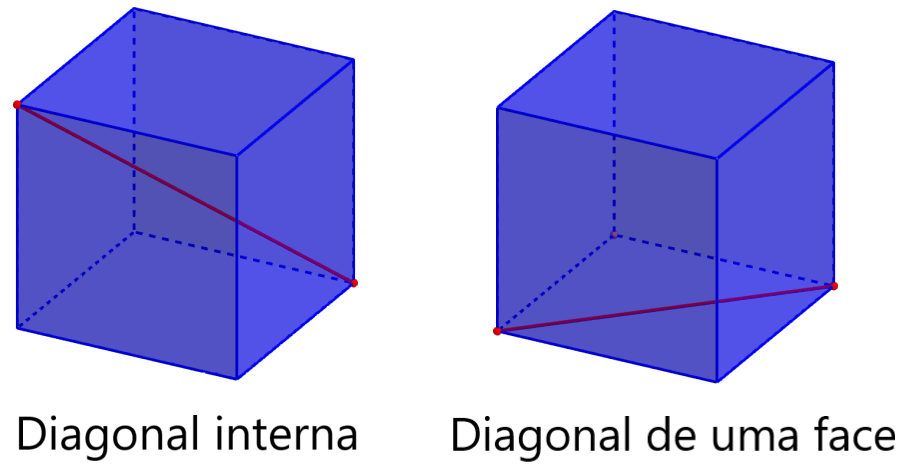
Para calcular a diagonal de uma face do cubo, temos que usar o teorema de Pitágoras uma vez. No entanto, para calcular a diagonal interna, precisamos usar o teorema de Pitágoras duas vezes. Então, fazemos isso em dois passos:
Passo 1: Calculamos a diagonal de uma face. Todas as faces de um cubo são quadradas, então temos o seguinte:
Para encontrar essa distância, temos que usar o teorema de Pitágoras. Se usarmos c para representar a diagonal, teremos o seguinte:
$latex {{c}^2}={{a}^2}+{{a}^2}$
$latex {{c}^2}=2{{a}^2}$
$latex c=\sqrt{2{{a}^2}}$
| $latex c=\sqrt{2}~a$ |
Então, encontramos uma fórmula para a diagonal da face.
Passo 2: Para encontrar uma expressão para a diagonal interna, temos que usar outro triângulo retângulo. Usamos a diagonal de uma face como a base do triângulo, um lado do cubo como a altura do triângulo e a diagonal interna como a hipotenusa:
Temos que usar o teorema de Pitágoras novamente para encontrar o comprimento da diagonal representada por d, então temos:
$latex {{d}^2}={{a}^2}+{{(\sqrt{2}~a)}^2}$
$latex {{d}^2}={{a}^2}+2{{a}^2}$
$latex {{d}^2}=3{{a}^2}$
$latex d=\sqrt{3{{a}^2}}$
| $latex d=\sqrt{3}~a$ |
Encontramos a fórmula para a diagonal interna de um cubo.
Exercícios de diagonal do cubo resolvidos
Os seguintes exercícios com as diagonais do cubo podem ser usados para praticar o uso da fórmula derivada acima. É recomendável que você tente resolver os exercícios sozinho antes de procurar a solução.
EXERCÍCIO 1
Qual é a diagonal de um cubo com lados de 5 m de comprimento?
Solução
Podemos usar a fórmula da diagonal com $latex a = 5$. Então, temos:
$latex d=\sqrt{3}~a$
$latex d=\sqrt{3}(5)$
$latex d= 8,66$
A diagonal mede 8,66 m.
EXERCÍCIO 2
Se um cubo tem lados de 6 m de comprimento, qual é sua diagonal?
Solução
Usamos o valor $latex a = 6$ na fórmula da diagonal. Então, temos:
$latex d=\sqrt{3}~a$
$latex d=\sqrt{3}(6)$
$latex d= 10,4$
A diagonal tem comprimento de 10,4 m.
EXERCÍCIO 3
Um cubo tem lados com 21 cm de comprimento. Qual é a sua diagonal?
Solução
Temos o comprimento $latex a = 21$, então usamos este valor na fórmula da diagonal:
$latex d=\sqrt{3}~a$
$latex d=\sqrt{3}(21)$
$latex d= 36,37$
A diagonal mede 36,37 cm.
EXERCÍCIO 4
Se a diagonal de um cubo é de 10 m, qual é o comprimento de seus lados?
Solução
Neste caso, temos o comprimento da diagonal e queremos encontrar o comprimento dos lados, então usamos $latex d = 10$ e resolvemos para a:
$latex d=\sqrt{3}~a$
$latex 10=\sqrt{3}~a$
$latex a= \frac{10}{\sqrt{3}}$
$latex a=5,77$
Os lados têm 5,77 m de comprimento.
EXERCÍCIO 5
Qual é o comprimento dos lados de um cubo que tem diagonal de 20 m?
Solução
Usamos o comprimento da diagonal $latex d = 20$ e resolvemos para a:
$latex d=\sqrt{3}~a$
$latex 20=\sqrt{3}~a$
$latex a= \frac{20}{\sqrt{3}}$
$latex a=11,55$
Os lados têm 11,55 m de comprimento.
Exercícios de diagonal do cubo para resolver
Pratique o uso da fórmula da diagonal do cubo para resolver os exercícios a seguir. Selecione uma resposta e verifique se você obteve a resposta correta.
Veja também
Você quer aprender mais sobre cubos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
