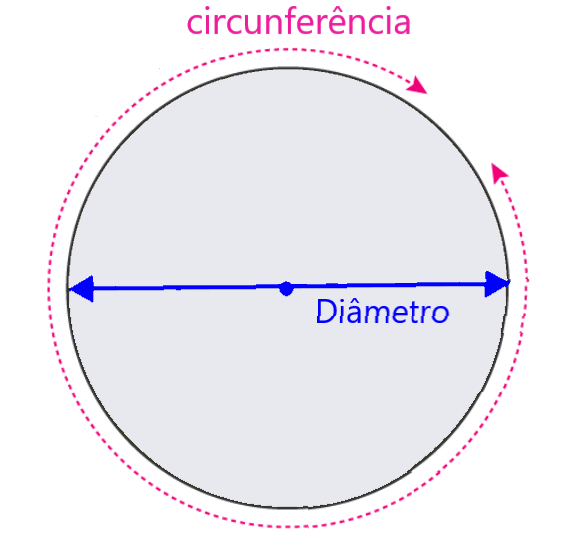
A circunferência de um círculo define o comprimento do contorno do círculo. A circunferência também é conhecida como perímetro do círculo, pois é uma medida dos limites do círculo. A circunferência pode ser calculada usando o comprimento do diâmetro ou o comprimento do raio e a constante π.
A seguir, aprenderemos sobre a circunferência do círculo com mais detalhes. Descobriremos qual é sua fórmula e conheceremos sua origem. Além disso, saberemos sobre a origem da constante π. Finalmente, resolveremos alguns exercícios onde aplicaremos a fórmula da circunferência.
GEOMETRIA
Relevante para…
Aprender sobre a circunferência de um círculo com exercícios.
GEOMETRIA
Relevante para…
Aprender sobre a circunferência de um círculo com exercícios.
Fórmula para a circunferência de um círculo
A circunferência representa o comprimento obtido dando uma volta completa ao redor do círculo. Este comprimento pode ser obtido usando o comprimento do diâmetro ou raio do círculo e a constante pi.
Lembre-se de que usamos a letra grega π para representar essa constante e que ela tem um valor aproximado de 3,141592… Para obter uma fórmula para a circunferência, podemos considerar o seguinte círculo:
No diagrama, podemos ver que a circunferência é a distância ao redor do círculo. Além disso, podemos ver que o diâmetro é a distância que passa pelo centro do círculo e conecta duas partes opostas da circunferência.
A constante π representa a razão entre a circunferência do círculo e o diâmetro. Isso significa que quando dividimos a circunferência de qualquer círculo pelo diâmetro, obtemos a constante π. Podemos expressar essa relação com a seguinte fórmula:
$latex \frac{C}{d}=\pi$
onde, C representa a circunferência e d é o comprimento do diâmetro do círculo. Além disso, podemos reescrever esta expressão da seguinte maneira:
| $latex C=\pi d$ |
Circunferência de um círculo com raio
A circunferência de um círculo também pode ser calculada usando o comprimento do raio. Para isso, usamos a relação $latex d=2r$. Ao reescrever a expressão, temos:
| $latex C=2\pi r$ |
Exercícios de circunferência de círculos resolvidos
Os exercícios a seguir são resolvidos usando as fórmulas para a circunferência dos círculos. Recomenda-se que você mesmo resolva os exercícios antes de procurar a solução.
EXERCÍCIO 1
Qual é a circunferência de um círculo com diâmetro de 5 m?
Solução
Temos o comprimento do diâmetro $latex d = 5$. Então, usamos a primeira fórmula:
$latex C=\pi d$
$latex C=\pi (5)$
$latex C=15,7$
A circunferência é igual a 15,7 m.
EXERCÍCIO 2
Se um círculo tiver um diâmetro de 9 m. Qual é o comprimento de sua circunferência?
Solução
Podemos usar a fórmula da primeira circunferência com o valor $latex d = 9$:
$latex C=\pi d$
$latex C=\pi (9)$
$latex C=28,3$
A circunferência é igual a 28,3 m.
EXERCÍCIO 3
Qual é o comprimento da circunferência de um círculo com raio de 4 m?
Solução
Aqui, temos o comprimento do raio em vez do diâmetro. Podemos usar a segunda fórmula com o valor $latex r=4$:
$latex C=2\pi r$
$latex C=2\pi (4)$
$latex C=50,3$
O comprimento da circunferência é de 50,3 m.
EXERCÍCIO 4
Um círculo tem um raio de 11 m. Qual é a sua circunferência?
Solução
Usamos a fórmula da segunda circunferência com o valor $latex r = 11$. Então, temos:
$latex C=2\pi r$
$latex C=2\pi (11)$
$latex C=69,1$
A circunferência é igual a 69,1 m.
EXERCÍCIO 5
Se um círculo tem uma circunferência de 80 m, qual é o comprimento de seu diâmetro?
Solução
Aqui, começamos com o valor da circunferência e queremos encontrar o comprimento do diâmetro, então usamos o valor $latex C = 80$ na fórmula e resolvemos para d:
$latex C=\pi d$
$latex 80=\pi d$
$latex d=\frac{80}{\pi}$
$latex d=25,5$
O comprimento do diâmetro é igual a 25,5 m.
Exercícios de circunferência de círculos para resolver
Use as fórmulas da circunferência dos círculos para resolver os exercícios a seguir. Se precisar de ajuda com isso, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre círculos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
