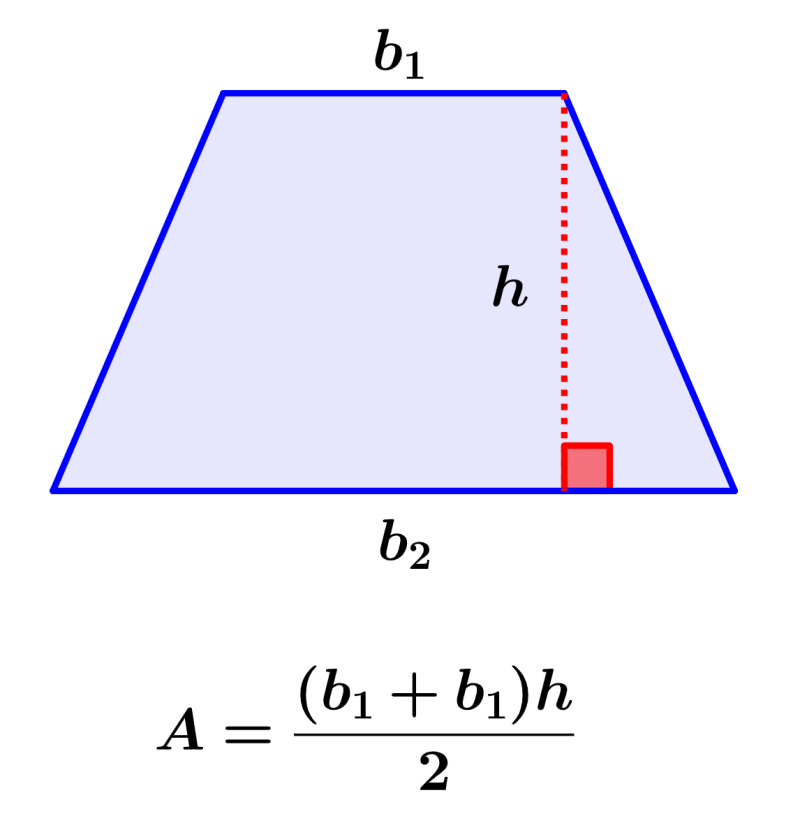
A área de um trapézio é a região coberta pelo trapézio em um plano bidimensional. Um trapézio é uma figura 2D que se enquadra na categoria de quadriláteros. Em um trapézio, um par de lados é paralelo e o outro par de lados não é paralelo. Semelhante a outras figuras geométricas, o trapézio também tem suas próprias propriedades e fórmulas baseadas em área e perímetro.
A seguir, conheceremos a fórmula para a área de um trapézio. Além disso, veremos alguns exercícios nos quais aplicaremos esta fórmula para encontrar a área.
Como calcular a área de um trapézio?
Para encontrar a área de um trapézio, calculamos a soma de suas bases, multiplicamos essa soma pela altura do trapézio e dividimos o resultado por 2. A fórmula para a área do trapézio é:
| $latex A=\frac{(b_{1}+b_{2})h}{2}$ |
onde,
- $latex b_{1}=$ o comprimento da base 1 do trapézio
- $latex b_{2}=$ o comprimento da base 2 do trapézio
- $latex h=$ o comprimento da altura do trapézio
Cada base do trapézio deve ser perpendicular à altura. Na figura, podemos ver que ambas as bases são lados do trapézio. No entanto, como os lados laterais não são perpendiculares a nenhuma das bases, uma linha tracejada é desenhada para representar a altura.
Derivação da fórmula para a área de um trapézio
Vamos usar a seguinte figura para derivar a fórmula para a área de um trapézio:
A área de um trapézio é igual à soma das áreas dos dois triângulos e a área do retângulo. Então, sabemos que:
área do trapézio = área do triângulo 1 + área do retângulo + área do triângulo 2
$latex A=\frac{ah}{2}+b_{1}h+\frac{ch}{2}$
$latex A=\frac{ah+2b_{1}h+ch}{2}$
Podemos simplificar a expressão e reorganizar os termos para obter:
$latex A=\frac{h}{2}(b_{1}+(a+b_{1}+c))$
Se usarmos $latex b_{2}$ para representar a base mais longa do trapézio, temos:
$latex b_{2}=a+b_{1}+c$
Substituindo isso na equação anterior, temos:
$latex A=\frac{h}{2}(b_{1}+b_{2})$
Portanto, a área do trapézio com bases $latex b_{1}, ~b_{2}$ e altura $latex h$ é $latex A=\frac{h}{2}(b_{1}+b_{2})$.
Exercícios de área de um trapézio resolvidos
Os exercícios a seguir podem ser usados para praticar a aplicação da fórmula para a área de um trapézio. Tente resolver os exercícios sozinho antes de olhar o resultado.
EXERCÍCIO 1
Encontre a área de um trapézio que tem bases de comprimento de 8 me 12 m e altura de 10 m.
Solução
Temos os seguintes dados:
- Base 1, $latex b_{1}=8$ m
- Base 2, $latex b_{2}=12$ m
- Altura, $latex h=10$ m
Portanto, usamos a fórmula da área, substituindo os dados fornecidos:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(8+12)10}{2}$
$latex =\frac{(20)(10)}{2}$
$latex =\frac{200}{2}$
$latex A=100$
A área do trapézio é de 100 m².
EXERCÍCIO 2
Qual é a área de um trapézio que tem bases de 11 m de comprimento e 15 m de altura e 12 m de altura?
Solução
A pergunta nos dá as seguintes informações:
- Base 1, $latex b_{1}=11$ m
- Base 2, $latex b_{2}=15$ m
- Altura, $latex h=12$ m
Usando as informações fornecidas, temos:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(11+15)12}{2}$
$latex =\frac{(26)(12)}{2}$
$latex =\frac{312}{2}$
$latex A=156$
A área do trapézio é de 156 m².
EXERCÍCIO 3
Um trapézio tem uma área de 200 cm², uma base de 9 cm de comprimento e a outra base de 11 cm de comprimento. Qual é a altura do trapézio?
Solução
Temos as seguintes informações:
- Área, $latex A=200$ cm²
- Base 1, $latex b_{1}=9$ cm
- Base 2, $latex b_{2}=11$ cm
Para encontrar a altura, usamos a fórmula da área e resolvemos para h:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex 200=\frac{(9+11)h}{2}$
$latex 400=(9+11)h$
$latex 400=20h$
$latex h=20$
A altura do trapézio é de 20 cm.
EXERCÍCIO 4
Um trapézio tem uma área de 240 m², uma base de 11 m de comprimento e a outra de 13 m de comprimento. Qual é a altura do trapézio?
Solução
A partir da pergunta, podemos obter os seguintes valores:
- Área, $latex A=240$ m²
- Base 1, $latex b_{1}=11$ m
- Base 2, $latex b_{2}=13$ m
Usamos a fórmula com os valores fornecidos e resolvemos para h:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex 240=\frac{(11+13)h}{2}$
$latex 480=(11+13)h$
$latex 480=24h$
$latex h=20$
A altura do trapézio é de 20 m.
EXERCÍCIO 5
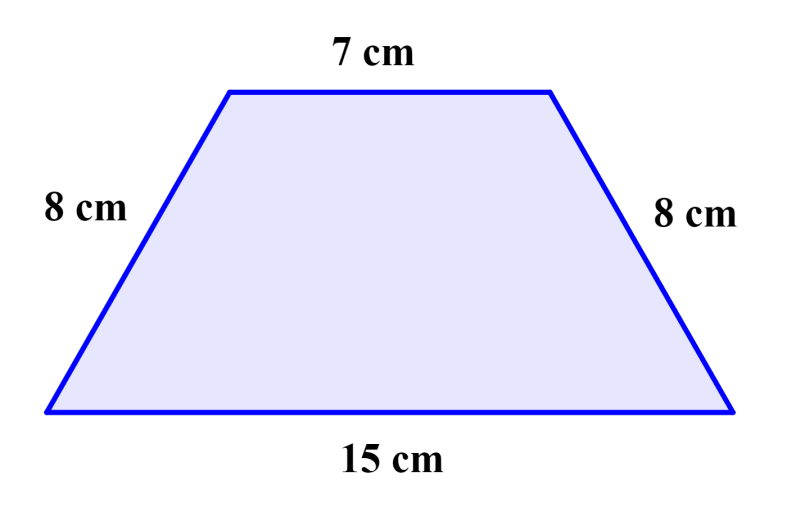
Encontre a área do seguinte trapézio:
Solução
Uma vez que os lados não paralelos do trapézio são iguais, a altura pode ser calculada da seguinte forma:
Obtemos as bases dos dois triângulos subtraindo 7 de 15 e dividindo por 2.
⇒ $latex \frac{15-7}{2}=4$ cm
Agora, podemos usar o Teorema de Pitágoras para encontrar a altura. Então, temos:
$latex {{8}^2}={{h}^2}+{{4}^2}$
$latex 64={{h}^2}+16$
$latex {{h}^2}=48$
$latex h=6.93$ cm
A altura do trapézio é de 6,93 cm. Agora, calculamos a área com estes valores:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(15+7)6.93}{2}$
$latex =\frac{(22)(6.93)}{2}$
$latex A=76.23$
A área do trapézio é de 76,23 cm².
Exercícios de área de um trapézio para resolver
Coloque em prática o que você aprendeu sobre a área do trapézio para resolver os exercícios a seguir. Selecione uma resposta e verifique-a para se certificar de que selecionou a correta.
Veja também
Você quer aprender mais sobre trapézios? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
