O apótema de um pentágono é a distância perpendicular do centro do pentágono ao centro de um de seus lados. O apótema também pode ser considerado como o raio do incircle de um polígono. O apótema é usado principalmente para calcular a área de um polígono regular.
A seguir, aprenderemos como calcular o apótema de um pentágono. Além disso, usaremos a fórmula do apótema para resolver alguns exercícios.
Fórmula para o apótema de um pentágono
Para encontrar a fórmula do apótema, podemos usar a imagem de um pentágono:
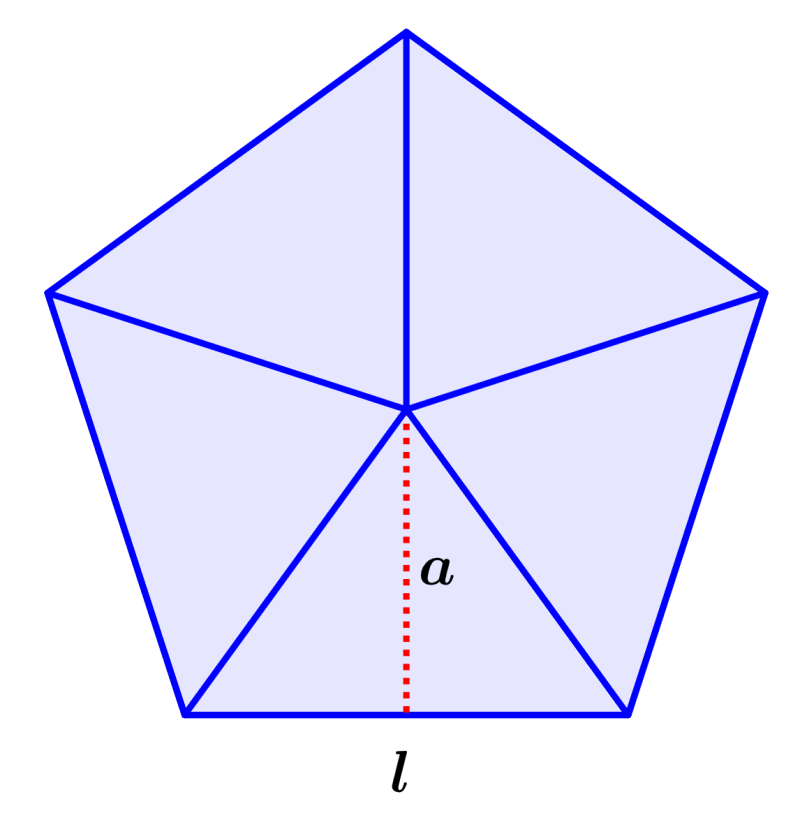
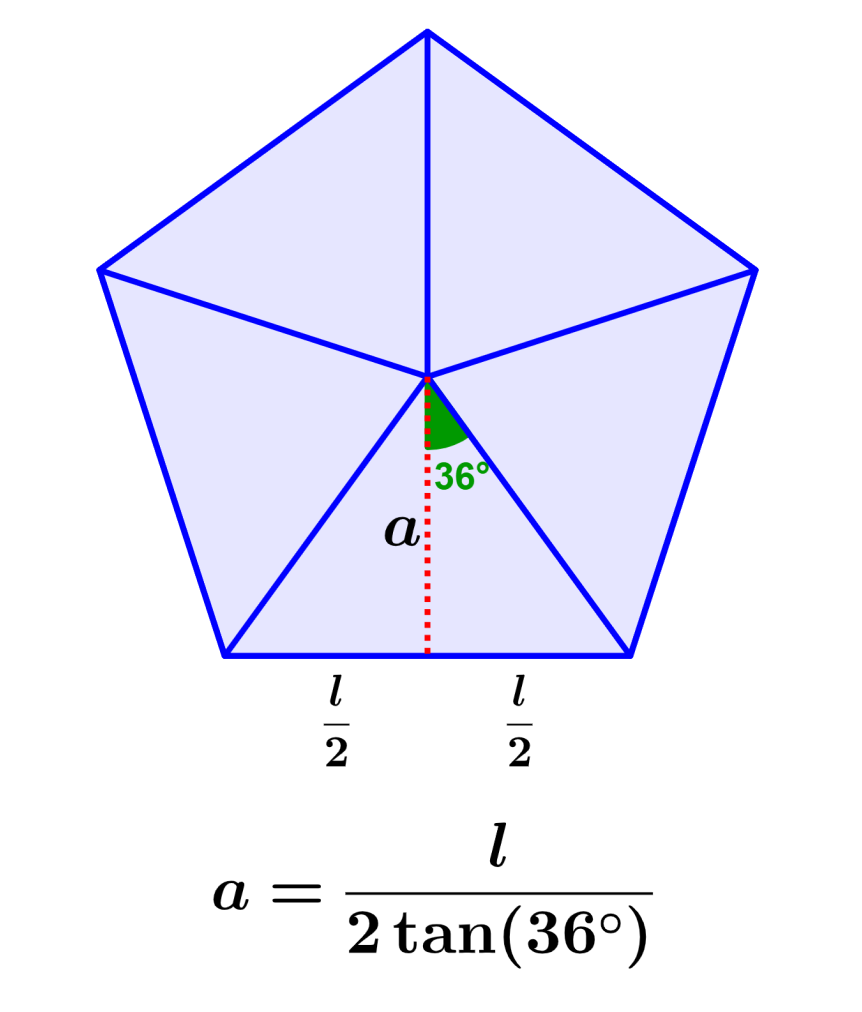
Aqui, dividimos o pentágono em cinco triângulos congruentes e usamos um dos triângulos para encontrar o apótema. Podemos ver que o apótema tem a altura de um dos triângulos e divide um dos lados em duas partes iguais.
Podemos usar trigonometria para encontrar o comprimento do apotema. Começamos encontrando o ângulo do centro do apótema. Temos cinco triângulos e, dividindo cada triângulo em dois, teríamos 10 pequenos triângulos.
Além disso, sabemos que uma volta completa tem 360°, então, dividindo pelos 10 triângulos, temos 36°. O ângulo no centro do pentágono sempre mede 36°.
Usamos a tangente para calcular a altura do triângulo. Em um triângulo retângulo, a tangente de um ângulo é igual ao comprimento do lado oposto dividido pelo comprimento do lado adjacente.
O lado oposto ao ângulo de 36° é a base do triângulo (metade do comprimento de um lado do pentágono). O lado adjacente ao ângulo de 36° é a altura do triângulo. Então, temos:
$latex \tan(36°)= \frac{ \text{oposto}}{ \text{adjacente}}$
$latex \tan(36°)= \frac{ \frac{l}{2}}{a}$
$latex \tan(36°)= \frac{l}{2a}$
$latex a= \frac{l}{2\tan(36°)}$
onde, a representa o comprimento do apótema e l representa o comprimento de um dos lados do pentágono.
Exercícios de apótema de pentágonos resolvidos
A fórmula para o apótema de um pentágono é usada para resolver os exercícios a seguir. Cada exercício tem sua respectiva solução, mas é recomendável que você tente resolver os exercícios antes de olhar a resposta.
EXERCÍCIO 1
Qual é o comprimento do apótema de um pentágono que tem lados de 4 m?
Solução
Usamos a fórmula do apótema com $latex l = 4$. Então, temos:
$latex a= \frac{l}{2 \tan(36°)}$
$latex a= \frac{4}{2 \tan(36°)}$
$latex a= \frac{4}{1,453}$
$latex a=2,75$
O comprimento do apótema é 2,75 m.
EXERCÍCIO 2
O comprimento dos lados de um pentágono é de 5 m. Qual é o comprimento do apótema?
Solução
Temos que os lados têm um comprimento de $latex l = 5$. Então, usando esse valor na fórmula, temos:
$latex a= \frac{l}{2 \tan(36°)}$
$latex a= \frac{5}{2 \tan(36°)}$
$latex a= \frac{5}{1,453}$
$latex a=3,44$
O comprimento do apótema é 3,44 m.
EXERCÍCIO 3
Um pentágono tem lados com 10 m de comprimento. Qual é o comprimento do seu apótema?
Solução
Aqui, o comprimento dos lados do pentágono é $latex l = 10$. Então, substituindo esse valor na fórmula, temos:
$latex a= \frac{l}{2 \tan(36°)}$
$latex a= \frac{10}{2 \tan(36°)}$
$latex a= \frac{10}{1,453}$
$latex a=6,88$
O comprimento do apótema é 6,88 m.
EXERCÍCIO 4
Um pentágono tem um apótema de comprimento de 7,6. Qual é o comprimento de seus lados?
Solução
Neste caso, começamos com o comprimento do apótema e queremos saber o comprimento dos lados do pentágono. Portanto, usamos a fórmula com $latex a = 7,6$ e resolvemos para l:
$latex a= \frac{l}{2 \tan(36°)}$
$latex 7,6= \frac{l}{2 \tan(36°)}$
$latex 7,6= \frac{l}{1,453}$
$latex l= (7,6)(1,453)$
$latex a=11,04$
O comprimento das laterais é de 11,04 m.
EXERCÍCIO 5
O que é o comprimento dos lados de um pentágono que tem uma apótema com comprimento de 6 m?
Solução
Novamente, começamos com o comprimento do apótema e vamos encontrar o comprimento dos lados do pentágono. Portanto, usamos o valor $latex a = 6$ na fórmula e resolvemos para l:
$latex a= \frac{l}{2 \tan(36°)}$
$latex 6= \frac{l}{2 \tan(36°)}$
$latex 6= \frac{l}{1,453}$
$latex l= (6)(1,453)$
$latex a=8,72$
O comprimento dos lados é de 8,72 m.
Exercícios do apótema de pentágonos para resolver
Coloque em prática o uso da fórmula do apótema dos pentágonos para resolver os exercícios seguintes. Se precisar de ajuda, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre pentágonos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
