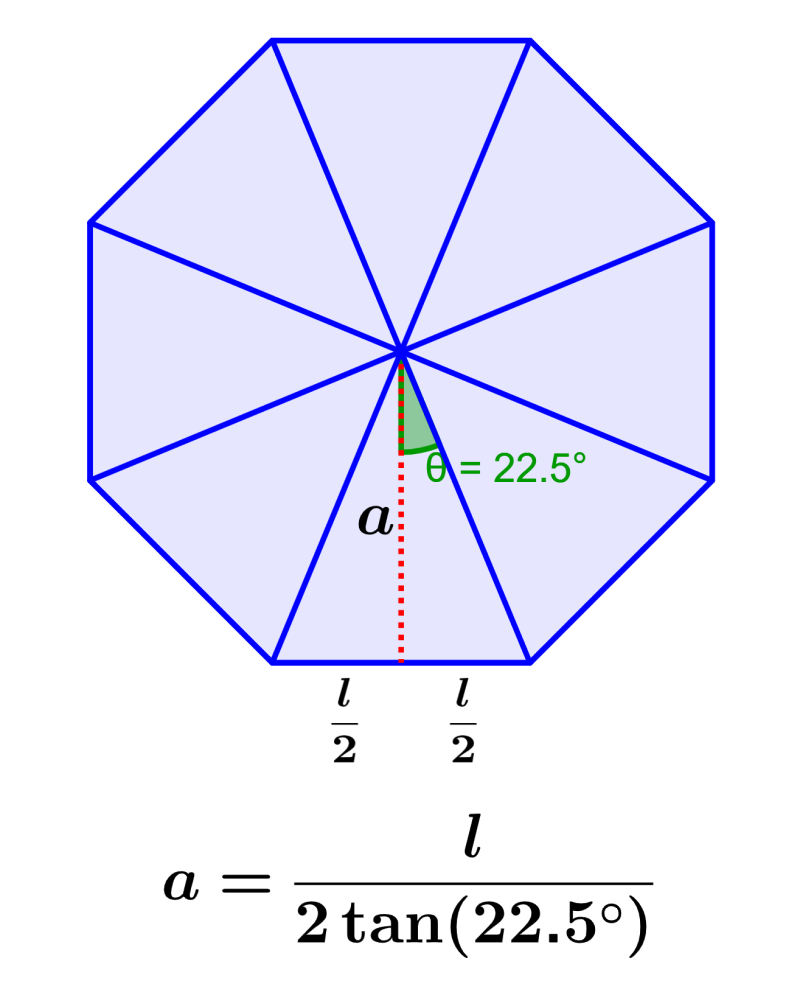
O apótema de qualquer polígono é igual à linha que conecta o centro do polígono a um de seus lados perpendicularmente. Usando o apótema, podemos calcular a área dos polígonos de uma maneira mais fácil. Podemos encontrar uma fórmula para o apótema de um octógono dividindo o octógono em oito triângulos congruentes e usando a trigonometria para determinar a altura de um dos triângulos, uma vez que é equivalente ao apótema.
A seguir, derivaremos uma fórmula para o apotema do octógono usando trigonometria. Além disso, vamos aplicar esta fórmula para resolver alguns exercícios.
Fórmula para o apótema de um octógono
Podemos encontrar uma fórmula para o apótema de um octógono usando trigonometria. Para isso, começamos dividindo o octógono em oito triângulos congruentes:
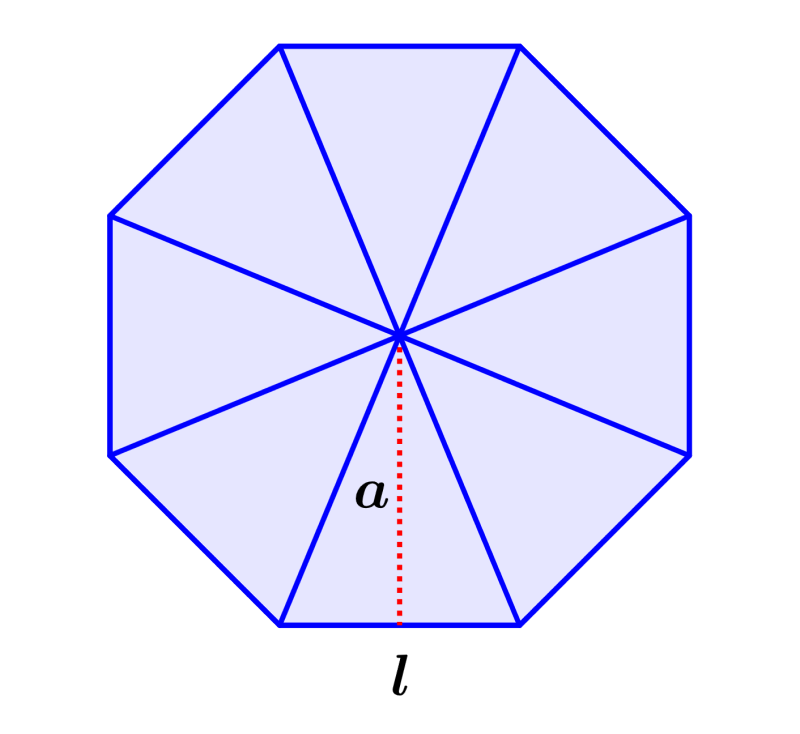
Vemos que o apótema divide o triângulo em dois pequenos triângulos retângulos. Podemos ver que a altura do triângulo é igual ao apótema, então podemos encontrar uma expressão para o apótema usando trigonometria. Precisamos encontrar a medida do ângulo central de um dos triângulos retângulos.
Sabemos que o ângulo central do octógono é igual a 360°. Além disso, sabemos que temos 16 pequenos triângulos retângulos, então o ângulo central de cada um é $latex 360 \div 16 = 22,5$°:
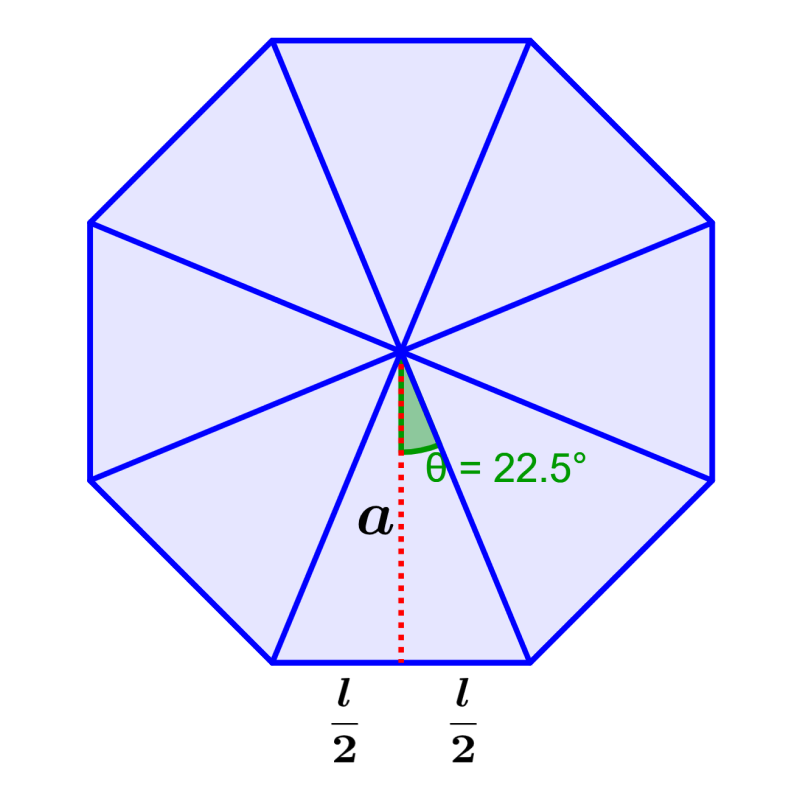
Agora que temos o ângulo, podemos usar a função tangente, que nos diz que a tangente do ângulo é igual ao lado oposto do lado adjacente. Então, temos:
$$\tan(22,5)=\frac{\text{oposto}}{\text{adjacente}}$$
$$\tan(22,5)=\frac{\frac{l}{2}}{a}$$
$$ \tan(22,5)=\frac{l}{2a}$$
| $$a=\frac{l}{2\tan(22,5)}$$ |
Exercícios de apótema de octógonos resolvidos
A fórmula do apótema do octógono é usada para resolver os exercícios a seguir. Cada exercício tem sua respectiva solução, mas é recomendável que você tente resolver os exercícios primeiro.
EXERCÍCIO 1
Um octógono tem lados de 4 m de comprimento. Qual é o seu apótema?
Solução
Usando a fórmula do apótema com o comprimento $latex l = 4$, temos:
$latex a=\frac{l}{2\tan(22,5°)}$
$latex a=\frac{4}{2\tan(22,5°)}$
$latex a=\frac{4}{0,828}$
$latex a=4,83$
O comprimento do apótema é 4,83 m.
EXERCÍCIO 2
Qual é o comprimento do apótema de um octógono com lados de 5 m?
Solução
Neste caso, temos o comprimento $latex l = 5$, então usamos a fórmula com este valor:
$latex a=\frac{l}{2\tan(22,5°)}$
$latex a=\frac{5}{2\tan(22,5°)}$
$latex a=\frac{5}{0,828}$
$latex a=6,04$
O comprimento do apótema é 6,04 m.
EXERCÍCIO 3
Um octógono tem lados de 9 m de comprimento. Qual é o seu apótema?
Solução
Podemos usar a fórmula do apótema com o comprimento $latex l = 9$. Então, temos:
$latex a=\frac{l}{2\tan(22,5°)}$
$latex a=\frac{9}{2\tan(22,5°)}$
$latex a=\frac{9}{0,828}$
$latex a=10,87$
O comprimento do apótema é 10,87 m.
EXERCÍCIO 4
Um octógono tem um apótema de 11,5 m de comprimento. Qual é o comprimento de seus lados?
Solução
Aqui, começamos com o comprimento do apótema e queremos encontrar o comprimento dos lados. Então, usamos a fórmula do apótema com $latex a = 11,5$ e resolvemos para l:
$latex a=\frac{l}{2\tan(22,5°)}$
$latex 11,5=\frac{l}{2\tan(22,5°)}$
$latex 11,5=\frac{l}{0,828}$
$latex l=11,5(0,828)$
$latex l=9,52$
O comprimento dos lados do octógono é de 9,52 m.
EXERCÍCIO 5
Qual é o comprimento dos lados de um octógono que possui um apótema de 15 m de comprimento?
Solução
Novamente, usamos a fórmula do apótema com $latex a = 15$ e resolvemos para l:
$latex a=\frac{l}{2\tan(22,5°)}$
$latex 15=\frac{l}{2\tan(22,5°)}$
$latex 15=\frac{l}{0,828}$
$latex l=15(0,828)$
$latex l=12,42$
O comprimento dos lados do octógono é de 12,42 m.
Exercícios do apótema de octógonos para resolver
Ponha em prática o uso da fórmula do apótema para resolver os exercícios seguintes. Se precisar de ajuda com isso, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre octógonos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
