O apótema de um hexágono é o comprimento da linha que une o centro do hexágono com o centro de um lado. O apótema é a linha perpendicular que conecta o centro do hexágono com um lado. O apótema pode ser muito útil quando queremos encontrar a área de um hexágono, pois nos permite usar uma fórmula mais simples. Podemos calcular o apótema dividindo o hexágono em seis triângulos congruentes e usando um dos triângulos. Podemos usar o teorema de Pitágoras ou trigonometria para derivar fórmulas diferentes.
A seguir, conheceremos as fórmulas do apótema de um hexágono. Além disso, resolveremos alguns exercícios usando essas fórmulas.
Fórmula para o apótema de um hexágono
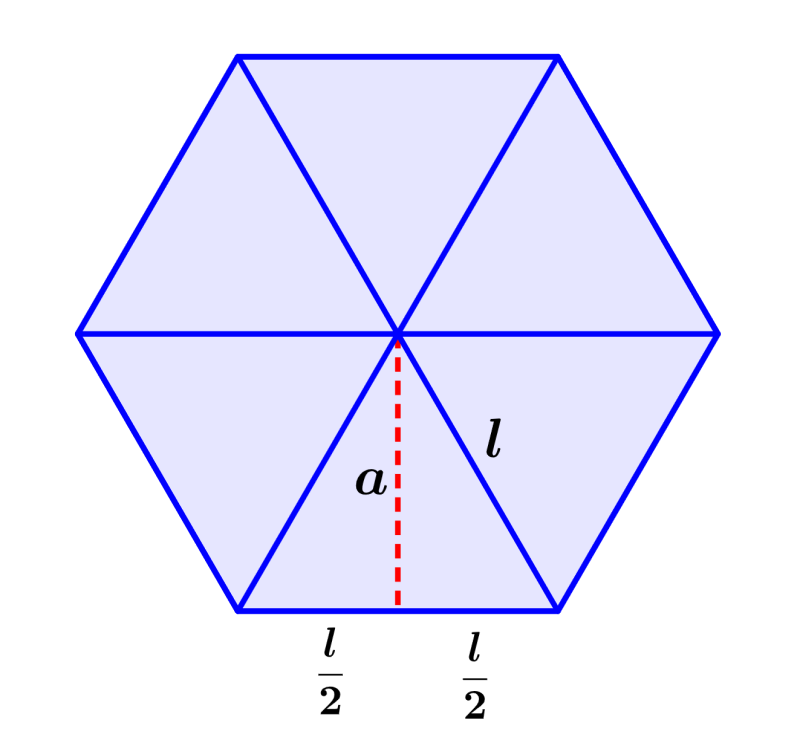
Existem dois métodos principais que podemos usar para derivar uma fórmula para o apótema do hexágono. Ambos os métodos envolvem a divisão do hexágono em seis triângulos congruentes, como na imagem a seguir:
Primeiro método: Podemos usar o teorema de Pitágoras em um dos triângulos formados. Sabemos que os triângulos formados são equiláteros, então seus três lados são iguais. Além disso, desenhando o apótema, vemos que ele divide a base em duas partes iguais como na imagem:
Então, usando esses comprimentos, temos:
$latex {{l}^2}={{a}^2}+{{(\frac{l}{2})}^2}$
$latex {{a}^2}={{l}^2}-{{(\frac{l}{2})}^2}$
$latex {{a}^2}={{l}^2}-\frac{{{l}^2}}{4}$
$latex {{a}^2}=\frac{3{{l}^2}}{4}$
| $latex a=\frac{\sqrt{3}l}{2}$ |
Segundo método: Semelhante ao método anterior, dividimos o hexágono em seis triângulos congruentes. Ao traçar o apótema, dividimos o triângulo ao meio, o que significa que se fizéssemos isso com todos os triângulos, teríamos 12 pequenos triângulos no total.
Para usar a trigonometria, temos que encontrar o ângulo central. Uma vez que o ângulo central total é igual a 360°, o ângulo central de cada pequeno triângulo mede $latex 360\div 12=30$°:
Agora, podemos usar a tangente. Sabemos que a tangente de um ângulo é igual ao lado oposto sobre o lado adjacente:
$latex \tan(30°)=\frac{\text{oposto}}{\text{adjacente}}$
$latex \tan(30°)=\frac{\frac{l}{2}}{a}$
$latex \tan(30°)=\frac{l}{2a}$
| $latex a=\frac{l}{2\tan(30°)}$ |
Exercícios de apótema de hexágonos resolvidos
Os exercícios a seguir usam ambas as fórmulas do apótema dos hexágonos vistos acima. Cada exercício tem sua respectiva solução, mas é recomendável que você tente resolver os exercícios antes de olhar o resultado.
EXERCÍCIO 1
Qual é o comprimento do apótema de um hexágono que tem lados de 6 m de comprimento?
Solução
Primeira fórmula: Usando a primeira fórmula com $latex l=6$, temos:
$latex a=\frac{\sqrt{3}l}{2}$
$latex a=\frac{\sqrt{3}(6)}{2}$
$latex a=5,2$
O comprimento do apótema é de 5,2 m.
Segunda fórmula: Usando a segunda fórmula com $latex l=6$, temos:
$latex a=\frac{l}{2\tan(30°)}$
$latex a=\frac{6}{2\tan(30°)}$
$latex a=5,2$
Vemos que obtivemos o mesmo resultado usando ambas as fórmulas.
EXERCÍCIO 2
Um hexágono tem lados de 8 m de comprimento. Qual é o comprimento do seu apótema?
Solução
Primeira fórmula: Podemos usar $latex l=8$ na primeira fórmula:
$latex a=\frac{\sqrt{3}l}{2}$
$latex a=\frac{\sqrt{3}(8)}{2}$
$latex a=6,93$
O comprimento do apótema é 6,93 m.
Segunda fórmula: Se agora usarmos a segunda fórmula com $latex l=8$, temos:
$latex a=\frac{l}{2\tan(30°)}$
$latex a=\frac{8}{2\tan(30°)}$
$latex a=6,93$
Temos o mesmo comprimento com ambas as fórmulas.
EXERCÍCIO 3
Qual é o comprimento do apótema de um hexágono com lados de 10 m de comprimento?
Solução
Primeira fórmula: Ao usar a primeira fórmula com $latex l=10$, temos:
$latex a=\frac{\sqrt{3}l}{2}$
$latex a=\frac{\sqrt{3}(10)}{2}$
$latex a=8,66$
O comprimento do apótema é de 8,66 m.
Segunda fórmula: Ao usar a segunda fórmula com $latex l=10$, temos:
$latex a=\frac{l}{2\tan(30°)}$
$latex a=\frac{10}{2\tan(30°)}$
$latex a=8,66$
O mesmo resultado foi obtido com ambas as fórmulas.
EXERCÍCIO 4
Qual é o comprimento dos lados de um hexágono que possui uma apótema de 7,5 m?
Solução
Neste caso, temos o comprimento do apótema e queremos encontrar o comprimento dos lados do hexágono.
Primeira fórmula: Usamos a primeira fórmula com $latex a=7,5$ e resolvemos para l:
$latex a=\frac{\sqrt{3}l}{2}$
$latex 7,5=\frac{\sqrt{3}l}{2}$
$latex 15=\sqrt{3}l$
$latex l=8,66$
O comprimento dos lados do hexágono é 8,66 m.
Segunda fórmula: Usamos a segunda fórmula com $latex a=7,5$ e resolvemos para l:
$latex a=\frac{l}{2\tan(30°)}$
$latex 7,5=\frac{l}{2\tan(30°)}$
$latex l=7,5(2\tan(30°))$
$latex l=8,66$
Temos o mesmo comprimento com ambas as fórmulas.
EXERCÍCIO 5
Qual é o comprimento dos lados de um hexágono que possui uma apotema de 12 m de comprimento?
Solução
Novamente, usamos ambas as fórmulas e resolvemos para l.
Primeira fórmula: Substituímos $latex a=12$ e resolvemos para l:
$latex a=\frac{\sqrt{3}l}{2}$
$latex 12=\frac{\sqrt{3}l}{2}$
$latex 24=\sqrt{3}l$
$latex l=13,87$
O comprimento dos lados do hexágono é de 13,87 m.
Segunda fórmula: Substituímos $latex a=12$ e resolvemos para l:
$latex a=\frac{l}{2\tan(30°)}$
$latex 12=\frac{l}{2\tan(30°)}$
$latex l=12(2\tan(30°))$
$latex l=13,86$
Nesse caso, obtivemos uma pequena diferença nas casas decimais. Isso se deve ao arredondamento utilizado na execução das operações.
Exercícios do apótema de hexágonos para resolver
Pratique usando as fórmulas do apótema do hexágono e resolva os seguintes exercícios. Selecione uma resposta e clique em “Verificar” para verificar sua resposta. Se precisar de ajuda com isso, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre hexágonos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
