O tetraedro regular é um dos cinco sólidos platônicos. Podemos pensar em um tetraedro como uma pirâmide triangular regular. Sua altura pode ser calculada usando uma fórmula derivada do teorema de Pitágoras.
A seguir, conheceremos a fórmula da altura de um tetraedro regular. Aprenderemos como derivar esta fórmula e aprenderemos a usá-la para resolver alguns exercícios práticos.
GEOMETRIA
Relevante para…
Aprender a calcular a altura de um tetraedro com exercícios.
GEOMETRIA
Relevante para…
Aprender a calcular a altura de um tetraedro com exercícios.
Fórmula para a altura de um tetraedro
Tetraedros são figuras tridimensionais que têm todas as faces com formato triangular. Tetraedros podem ser considerados como pirâmides triangulares regulares.
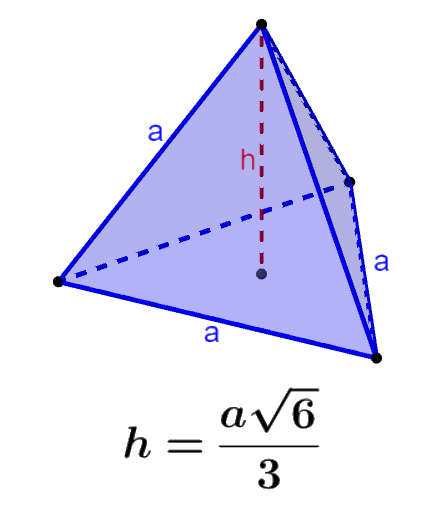
A altura de um tetraedro é o comprimento do segmento perpendicular à base e conectado ao vértice oposto. A fórmula para a altura de um tetraedro regular é:
| $latex h=\frac{a\sqrt{6}}{3}$ |
Prova da fórmula da altura de um tetraedro
Para derivar a fórmula para a altura de um tetraedro, consideramos a seguinte figura:
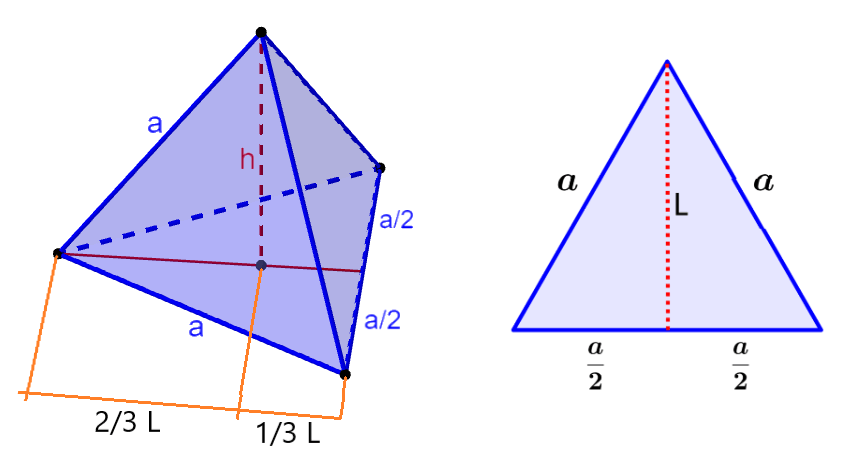
Podemos ver que a altura é o segmento perpendicular à base do tetraedro que une sua base com o vértice oposto. A partir do diagrama, vemos que a altura começa em 2/3 de L, onde L é a altura de uma face do tetraedro.
Podemos calcular o comprimento da altura do tetraedro usando o teorema de Pitágoras, onde a é a hipotenusa, h é um cateto e 2/3 de L é o outro cateto. Então temos
$latex {{h}^2}+{{(\frac{2}{3}L)}^2}={{a}^2}$
$latex {{h}^2}+\frac{4}{9}{{L}^2}={{a}^2}$
Agora considerando que as faces de um tetraedro regular são triângulos equiláteros, podemos encontrar uma expressão para L, lembrando que a altura de um triângulo equilátero é igual a $latex \frac{a~\sqrt{3}}{2}$.
Substituindo na equação, temos:
$latex {{h}^2}+\frac{4}{9}{{(\frac{a~\sqrt{3}}{2})}^2}={{a}^2}$
$latex {{h}^2}+\frac{4}{9}(\frac{{{a}^2}(3)}{4})={{a}^2}$
$latex {{h}^2}+\frac{{{a}^2}}{3}={{a}^2}$
$latex {{h}^2}={{a}^2}-\frac{{{a}^2}}{3}$
$latex {{h}^2}=\frac{2{{a}^2}}{3}$
$latex h=\frac{\sqrt{2{{a}^2}}}{\sqrt{3}}$
$latex h=\frac{a~\sqrt{2}}{\sqrt{3}}$
$latex h=\frac{a~\sqrt{2}(\sqrt{3})}{3}$
$latex h=\frac{a~\sqrt{6})}{3}$
Altura de um tetraedro – Exercícios resolvidos
A fórmula para a altura de um tetraedro é usada para resolver os seguintes exercícios. Tente resolver os exercícios antes de olhar para a resposta.
EXERCÍCIO 1
Se os lados de um tetraedro têm 4 m de comprimento, qual é a sua altura?
Solução
Temos que usar a fórmula da altura com o valor a=4. Então temos:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{4~\sqrt{6}}{3}$
$latex h=3,27$
A altura do tetraedro é de 3,27 m.
EXERCÍCIO 2
Determine a altura de um tetraedro que tem lados de comprimento 6 m.
Solução
Usando o valor a=6 na fórmula para a altura do tetraedro, temos:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{6~\sqrt{6}}{3}$
$latex h=4,9$
Portanto, a altura do tetraedro é de 4,9 m.
EXERCÍCIO 3
Qual é a altura de um tetraedro que tem lados de 10 cm de comprimento?
Solução
Vamos aplicar a fórmula para a altura de um tetraedro usando o valor a=10. Então temos
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{10~\sqrt{6}}{3}$
$latex h=8,16$
Portanto, a altura do tetraedro é 8,16 cm.
EXERCÍCIO 4
Se um tetraedro tem uma altura de 8 m, qual é o comprimento de um de seus lados?
Solução
Neste caso, sabemos o comprimento da altura e temos que calcular o comprimento de um dos lados. Então, temos que usar a fórmula da altura e resolver para a:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex 8=\frac{a~\sqrt{6}}{3}$
$latex 24=a~\sqrt{6}$
$latex a=9,8$
Assim, os lados do tetraedro têm 9,8 m de comprimento.
EXERCÍCIO 5
Um tetraedro tem uma altura com um comprimento de 15 cm. Determine o comprimento de seus lados.
Solução
Semelhante ao problema anterior, vamos usar a fórmula da altura para resolver a:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex 15=\frac{a~\sqrt{6}}{3}$
$latex 45=a~\sqrt{6}$
$latex a=18,37$
Os lados do tetraedro têm um comprimento de 18,37 m.
EXERCÍCIO 6
Qual é a altura de um tetraedro que tem lados de comprimento 11,5 cm?
Solução
Aplicando a fórmula da altura com o valor a=11,5, temos:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{11,5~\sqrt{6}}{3}$
$latex h=9,4$
Portanto, a altura do tetraedro é 9,4 cm.
EXERCÍCIO 7
Determine a altura de um tetraedro que tem comprimentos laterais de 24,5 m.
Solução
Usando o valor a=24,5 na fórmula para a altura do tetraedro, temos:
$latex h=\frac{a~\sqrt{6}}{3}$
$latex h=\frac{24.5~\sqrt{6}}{3}$
$latex h=20$
A altura do tetraedro é de 20 m.
Altura de um tetraedro – Exercícios para resolver
Use o que você aprendeu sobre a altura de um tetraedro para resolver os exercícios a seguir. Se você tiver problemas com esses exercícios, pode se orientar com os exercícios resolvidos acima.
Veja também
Interessado em aprender mais sobre tetraedros? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
