Fórmulas e propriedades de produto escalar de vetores

Produto escalar utilizando magnitudes e ângulos entre vetores

O produto escalar de dois vetores $latex \vec{A}$ e $latex \vec{B}$ é denotado por $latex \vec{A} \cdot \vec{B}$. O resultado do produto escalar é uma quantidade escalar.

Se conhecermos as magnitudes dos vetores e o ângulo entre suas direções, podemos aplicar a seguinte fórmula para encontrar seu produto escalar:

$$\vec{A}\cdot \vec{B}=AB\cos(\theta)$$

onde $latex A$ e $latex B$ são as magnitudes de $latex \vec{A}$ e $latex \vec{B}$ respectivamente, e $latex \theta$ é o ângulo entre os vetores.

Para entender esta fórmula, podemos desenhar os vetores $latex \vec{A}$ e $latex \vec{B}$ com seus pontos iniciais no mesmo lugar:

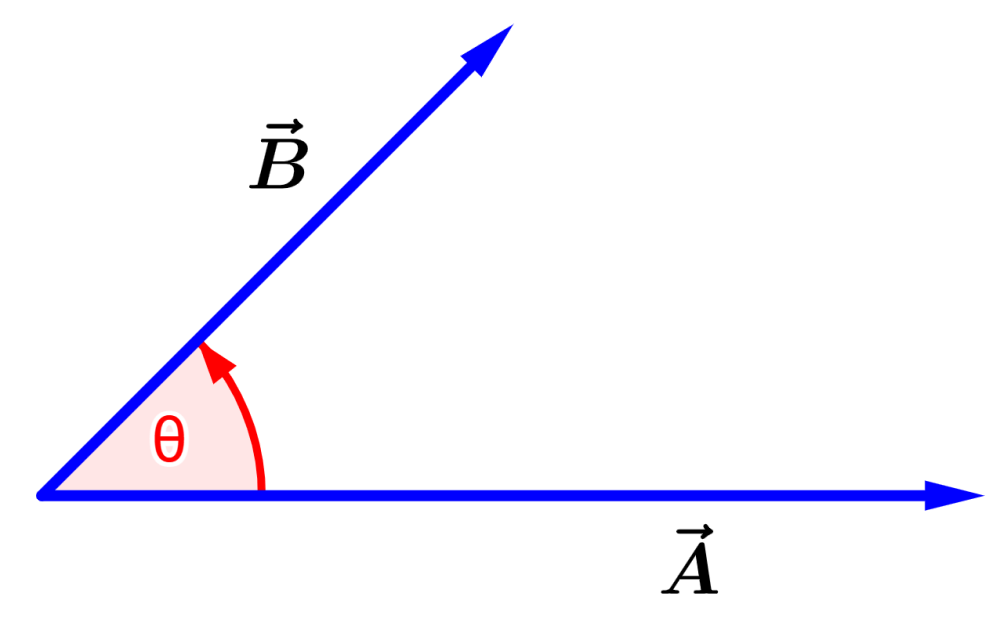
O ângulo $latex \theta$ representa o ângulo entre suas direções e pode variar de 0° a 180°. A figura a seguir mostra a projeção do vetor $latex \vec{B}$ na direção de $latex \vec{A}$:

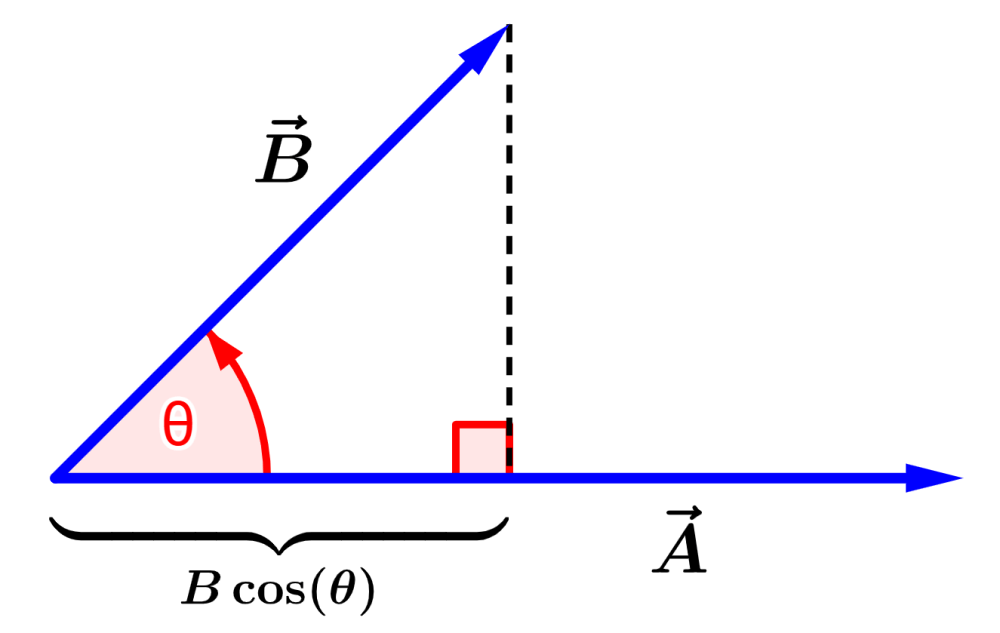
A projeção mostrada é a componente de $latex \vec{B}$ na direção de $latex \vec{A}$ e é igual a $latex B \cos(\theta)$.

A projeção mostrada é a componente de $latex \vec{B}$ na direção de $latex \vec{A}$ e é igual a $latex B \cos(\theta)$.

Alternativamente, também podemos definir $latex \vec{A}\cdot \vec{B}$ como a magnitude de $latex \vec{B}$ multiplicada pela componente de $latex \vec{A}$ na direção de $latex \vec{B}$.

Produto escalar de vetores usando seus componentes

O produto escalar de dois vetores $latex \vec{A} \cdot \vec{B}$ pode ser calculado com a seguinte fórmula se conhecermos os componentes $latex x,~y,~z$ dos vetores:

$$\vec{A}\cdot \vec{B}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}$$

Para demonstrar esta fórmula, podemos considerar o produto escalar dos vetores unitários $latex \hat{i},~\hat{j},~\hat{k}$.

Como todos os vetores unitários têm módulo igual a 1 e são perpendiculares entre si, temos:

$latex \hat{i}\cdot \hat{i}=\hat{j}\cdot \hat{j}=\hat{k}\cdot \hat{k}=(1)(1)\cos 0^{\circ}=1$

$latex \hat{i}\cdot \hat{j}=\hat{i}\cdot \hat{k}=\hat{j}\cdot \hat{k}=(1)(1)\cos 90^{\circ}=0$

Agora, escrevemos os vetores em termos de suas componentes, expandimos o produto e aplicamos os resultados das multiplicações dos vetores unitários para simplificar:

$$\vec{A}\cdot \vec{B}=(A_{x}\hat{i}+A_{y}\hat{j}+A_{z}\hat{k})\cdot (B_{x}\hat{i}+B_{y}\hat{j}+B_{z}\hat{k})$$

$$=A_{x}\hat{i}\cdot B_{x}\hat{i}+A_{x}\hat{i}\cdot B_{y}\hat{j}+A_{x}\hat{i}\cdot B_{z}\hat{k})$$

$$+A_{y}\hat{j}\cdot B_{x}\hat{i}+A_{y}\hat{j}\cdot B_{y}\hat{j}+A_{y}\hat{j}\cdot B_{z}\hat{k})$$

$$+A_{z}\hat{k}\cdot B_{x}\hat{i}+A_{z}\hat{k}\cdot B_{y}\hat{j}+A_{z}\hat{k}\cdot B_{z}\hat{k})$$

$$=A_{x}B_{x}\hat{i}\cdot\hat{i} +A_{x}B_{y}\hat{i}\cdot\hat{j}+A_{x}B_{z}\hat{i}\cdot\hat{k})$$

$$+A_{y}B_{x}\hat{j}\cdot\hat{i}+A_{y}B_{y}\hat{j}\cdot\hat{j}+A_{y}B_{z}\hat{j}\cdot\hat{k})$$

$$+A_{z}B_{x}\hat{k}\cdot\hat{i}+A_{z}B_{y}\hat{k}\cdot\hat{j}+A_{z}B_{z}\hat{k}\cdot\hat{k})$$

Usando os resultados dos produtos escalares dos vetores unitários vistos acima, seis desses nove termos são zero e temos:

$$\vec{A}\cdot \vec{B}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}$$

Propriedades de produto escalar de vetores

O produto escalar de vetores tem várias propriedades importantes. Seguem-se algumas delas:

Propriedade comutativa

O produto escalar é comutativo, o que significa que a ordem dos vetores não afeta o resultado. Então, temos:

$$\vec{A}\cdot \vec{B} = \vec{B} \cdot \vec{A}$$

Propriedade distributiva

O produto escalar é distributivo sobre a adição vetorial, o que significa que o produto escalar pode ser distribuído entre os termos da adição vetorial:

$$\vec{A} \cdot (\vec{B} + \vec{C}) = \vec{A} \cdot \vec{B} + \vec{A} \cdot \vec{C}$$

Multiplicação escalar

É possível multiplicar um vetor por um escalar antes ou após realizar o produto escalar, e o resultado será o mesmo.

$$(k\vec{A}) \cdot \vec{B} = k(\vec{A} \cdot \vec{B}) = \vec{A} \cdot (k\vec{B})$$

Vetores ortogonais

Se dois vetores são ortogonais (perpendiculares) entre si, seu produto escalar é zero. Alternativamente, se o produto escalar for zero, os vetores são ortogonais ou um deles é um vetor nulo.

$latex \vec{A} \cdot \vec{B} = 0$

se $latex \vec{A}$ é ortogonal a $latex \vec{B}$

Vetores paralelos

Se os vetores $latex \vec{A}$ e $latex \vec{B}$ são paralelos, o ângulo $latex \theta $ é igual a 0 e temos $latex \cos(\theta)=1$. Então:

$latex \vec{A} \vec{B}=|\vec{A}||\vec{B}|$

Produto escalar de um vetor com ele mesmo

O produto escalar de um vetor com ele mesmo é igual ao quadrado de sua magnitude. Isso decorre da propriedade anterior:

$latex \vec{A} \cdot \vec{A} =|\vec{A}|^2$

Produto escalar de vetores unitários

O produto escalar de um vetor unitário por ele mesmo é igual a 1 (a magnitude desses vetores é 1):

$latex \hat{i}\cdot \hat{i}=\hat{j}\cdot \hat{j}=\hat{k}\cdot \hat{k}=1$

O produto escalar de vetores unitários ortogonais é igual a 0:

$latex \hat{i}\cdot \hat{j}=\hat{i}\cdot \hat{k}=\hat{j}\cdot \hat{k}=0$

Relação com o ângulo entre os vetores

O produto escalar pode ser usado para encontrar o cosseno do ângulo entre dois vetores, o que serve para determinar o próprio ângulo:

$$\cos(\theta) = \frac{\vec{A} \cdot \vec{B}}{|\vec{A}||\vec{B}|}$$

Ver também

Interessado em saber mais sobre vectores? Pode visitar as seguintes páginas.

• Produto escalar de dois vetores – Exercícios resolvidos
• Produto vetorial de dois vetores – Exercícios resolvidos
• Fórmulas e propriedades de produto vetorial de vetores