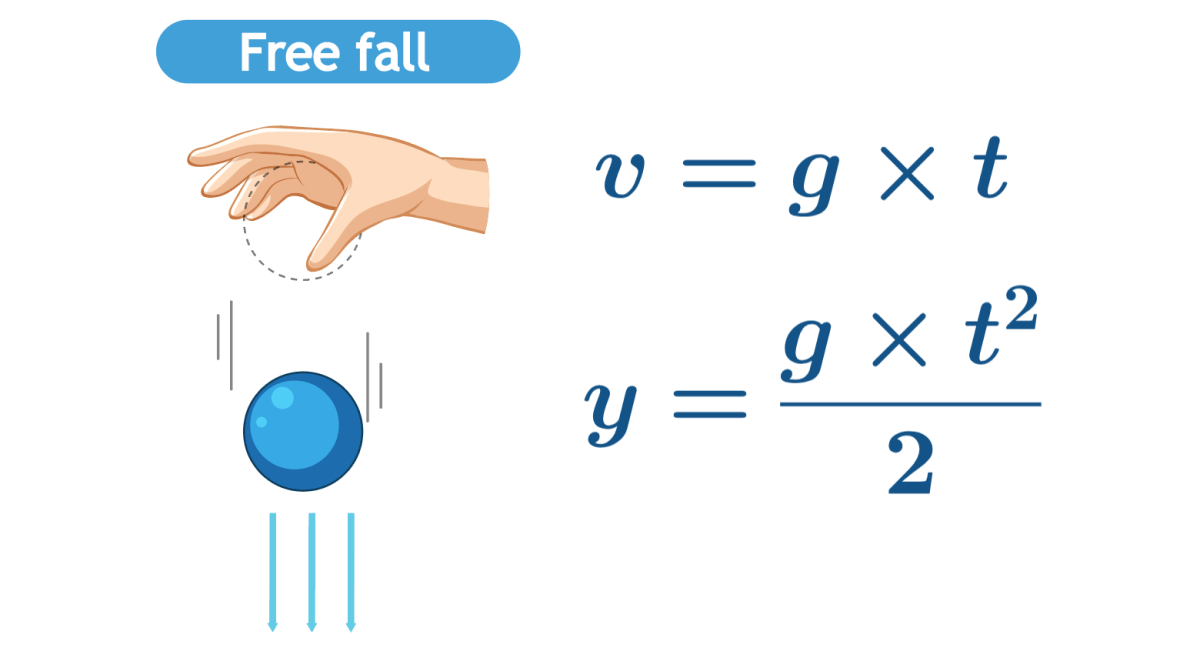Exercícios Resolvidos de Queda Livre em Física

A queda livre é um movimento retilíneo com aceleração constante, onde a aceleração vem da atração gravitacional da Terra. A coordenada vertical $latex y$ muda com o tempo $latex t$ à medida que o corpo desce, razão pela qual a posição vertical é considerada uma função do tempo dada pela seguinte expressão:

$$ y(t)= h + v_0 \cdot t + \frac{1}{2} \cdot (-g) \cdot t^2 $$

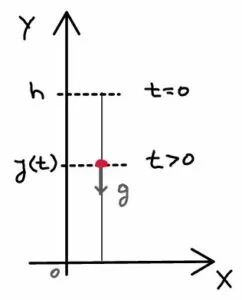
Na expressão anterior, $latex h$ representa a altura inicial, $latex v_0$ a velocidade inicial que, no caso de um objeto ser lançado, é zero ($latex v_0=0$). $latex g$ é a magnitude da aceleração da gravidade, um sinal de menos foi colocado porque essa aceleração sempre aponta para baixo, e como o eixo Y tem uma orientação positiva para cima, então para baixo é negativo. A posição da bola em qualquer momento $latex t$ é dada por $latex y(t)$ e é medida desde o solo até a posição atual da bola.

Suponha que a bola chegue ao solo no instante $latex t_s$, então para esse instante é verdade que $latex y(t_s)=0$:

$$ 0= h – \frac{1}{2} \cdot g \cdot {t_s}^2 $$

Resolvemos para a aceleração da gravidade $latex g$:

$$g=\dfrac{2 \cdot h}{{t_s}^2}$$

Usando os dados conhecidos para determinar o valor numérico de $latex g$:

$$g=\dfrac{2 \cdot 55,86 m}{{3.3764s}^2}=9,80 \frac{m}{s^2}$$

Levando em consideração que $latex 1m = 3,28084~ pés$, a aceleração da gravidade expressa em pés por segundo ao quadrado é:

$$ g= 9,80 \frac{m}{s^2} = 9,80 \frac{3,28084~ feet}{s^2}=32,15 \frac{feet}{s^2}$$

Escolhemos um sistema de coordenadas com a origem no nível do solo e a direção positiva do eixo Y para cima; nesse caso, a posição da bola em função do tempo é dada por:

$$ y(t)= h + v_0 \cdot t + \frac{1}{2} \cdot (-g) \cdot t^2 $$

No instante $latex t_s$, a bola chega ao chão. Usando os dados conhecidos, ficamos com:

$$ 0= 55,86 + 10 \cdot t_s – \frac{1}{2} \cdot 9,80 \cdot {t_s}^2 $$

Observe que o tempo $latex t_s$ satisfaz uma equação de segundo grau cujas soluções são:

$$t_s= \dfrac{-10 \pm \sqrt{10^2 – 4 \cdot (-9,80/2) \cdot 55,86}}{2 \cdot (-9,80/2)}$$

$$ t_s= \dfrac{-10 \pm \sqrt{100 +1094,86}}{ -9,80} $$

Essa equação tem duas soluções, mas estamos interessados apenas na solução positiva (aquela com o sinal negativo na frente da raiz), que é a solução após as operações terem sido realizadas:

$$ t_s=4,55 s$$

A velocidade da bola, imediatamente antes de tocar o solo, é dada por:

$$ v(t_s)=v_0-g \cdot t_s= 10 -9,80 \cdot 4,55= -34,59 \frac{m}{s}$$

Onde o sinal negativo no resultado da velocidade indica que a velocidade da bola imediatamente antes de atingir o solo está apontando para baixo.

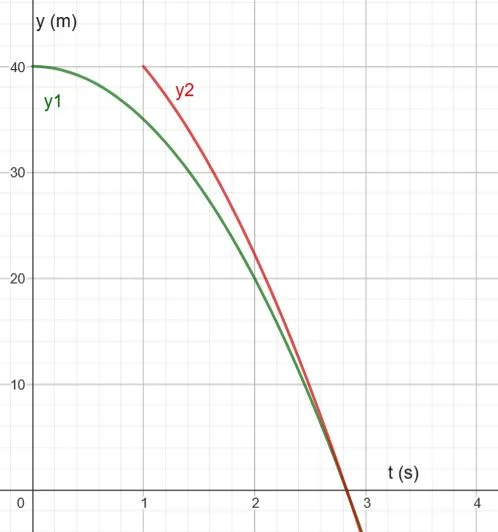
O eixo Y é escolhido com origem na superfície do rio e direção vertical para cima. As expressões que fornecem a coordenada Y de cada uma das pedras são:

$$ y_1(t) = h -\frac{1}{2} \cdot g \cdot t^2$$

$$y_2(t)= h \; – \; v_0 \cdot (t-t_o) -\frac{1}{2} \cdot g \cdot (t-t_o)^2$$

Sabemos que quando as pedras atingem a superfície da água do rio, sua coordenada Y é zero. Usando os dados conhecidos, temos:

$$ 0 = 40 -\frac{1}{2} \cdot 10 \cdot t_s^2$$

$$0= 40 \; – \; v_0 \cdot (t_s-1) -\frac{1}{2} \cdot 10 \cdot (t_s-1)^2$$

A partir da primeira equação, obtemos o tempo de chegada $latex t_s$:

$$ t_s= \sqrt{8} s=2,83 s$$

Em seguida, substituímos esse resultado na segunda expressão e resolvemos a velocidade $latex v_0$:

$$0= 40 \; – \; v_0 \cdot (1,83) -\frac{1}{2} \cdot 10 \cdot (1,83)^2 \; \Rightarrow \; 23,26 \; – \; v_0 \cdot 1,83=0 $$

A partir daí, obtemos o valor da velocidade com a qual a segunda pedra foi lançada:

$$ v_0=12,71 \frac{m}{s} $$

Primeiro, determinaremos a altura e a velocidade do foguete 40 segundos após o disparo. Para isso, usaremos um sistema de coordenadas com o eixo Y apontando para cima e com origem no solo.

Então, se o tempo t estiver entre 0s e 40s, a posição do foguete será dada por:

$$ y(t)= \frac{1}{2} \cdot a \cdot t^2$$

Isso significa que a altitude alcançada aos 40 segundos de voo foi:

$$ y(40s)= \frac{1}{2} \cdot 0.2 \cdot 40^2=160m$$

Atingindo uma velocidade de:

$$ v(40s) = 0,2 \frac{m}{s^2} \cdot 40 s= 8 \frac{m}{s}$$

Após 40 segundos, todo o movimento subsequente ocorre na aceleração da gravidade, que aproximaremos de $latex 10 \frac{m}{s^2}$.

A altura máxima ocorrerá quando a velocidade for cancelada por um instante, e chamaremos esse instante de $latex \tilde{t}$:

$$ v(\tilde{t})= 8 \frac{m}{s} – 10 \frac{m}{s^2} \cdot (\tilde{t}-40s)^2 = 0 \; \Rightarrow \tilde{t}=40,89s$$

A altura máxima alcançada será:

$$h_{max}=160m + 8 \frac{m}{s} \cdot 0,89s- \frac{1}{2} \cdot 10 \frac{m}{s^2} \cdot (0,89s)^2$$

$$ h_{max}=160,16 m$$

O tempo que leva para descer da altitude máxima é: $latex t_{des}=\sqrt{\dfrac{2 \cdot 160,16}{10}}=5,66s$

Então, o tempo total de voo foi: $latex t_v=40,89s + 5,66s=46,55s$

Usando as fórmulas de queda livre, podemos calcular a velocidade final ($latex v_f$) e o tempo ($latex t$) da seguinte forma:

• $latex v_f = \sqrt{2 * g * h}$
• $latex t =\sqrt{2 * h / g}$
• Substituindo os valores, obtemos:
  • $latex v_f = \sqrt{2 * 9,8 * 20} ≈ 19,8 m/s$
  • $latex t = \sqrt{2 * 20 / 9,8} ≈ 2,02 s$

.

Usando a fórmula de queda livre, podemos calcular a altura (h) do terraço da seguinte forma:

• $latex h = 0,5 * g * t^2$
• Substituindo os valores, obtemos:
  • $latex h = 0,5 * 9,8 * 6^2 ≈ 176,4 ~metros$

.

Usando a fórmula de queda livre, podemos calcular o tempo (t) que a bola leva para atingir sua altura máxima da seguinte forma:

• $latex v_f = v_i – g \cdot t$
• Quando a bola atinge sua altura máxima, sua velocidade final $latex v_f$ é igual a 0. Substituindo os valores, obtemos:
  • $latex 0 = 15 \; – 9,8 \cdot t$
  • $latex t = 15 / 9,8 ≈ 1,53 s$

.

Usando a fórmula de queda livre, que relaciona a velocidade final, a velocidade inicial e a altura, podemos calcular a altura máxima (h) atingida pela bola da seguinte forma:

• $latex {v_f}^2 = {v_i}^2 – 2 \cdot g \cdot h$
• Quando a bola atinge sua altura máxima, sua velocidade final ($latex v_f$) é igual a 0. Substituindo os valores, obtemos:
  • $latex 0 = 20^2 – 2 * 9,8 * h$
  • $latex h = 20^2 / (2 * 9,8) ≈ 20,41 ~metros$

.

Usaremos a expressão que fornece a posição vertical como uma função do tempo para um movimento com aceleração constante igual à aceleração da gravidade. Escolheremos o eixo Y apontando para cima e com origem no solo:

$$y(t)=y_0+v_0 \cdot t – \frac{1}{2} g \cdot t^2 $$

Se denotarmos por $latex \tilde t$ o instante em que a bola atinge o solo ($latex y(\tilde t)=0$), ficamos com:

$$0=10+25 \cdot \tilde t – \frac{1}{2} 10 \cdot {\tilde t}^2 $$

Esta é uma equação quadrática que tem duas soluções: i) $latex \tilde t=-0,372s$ e ii) $latex \tilde t=+5,372s$. O primeiro corresponde a um momento anterior ao lançamento da bola, portanto não tem significado físico. Por outro lado, a segunda solução corresponde ao instante em que a bola atinge o solo: $latex \tilde t=5,372s$

Escolhemos um sistema de coordenadas com o eixo Y verticalmente para cima e a origem na parte inferior (base) do penhasco. Assim, a posição da pedra em função do tempo, medida a partir do instante em que foi liberada, é dada por:

$$y(t)=y_0-\frac{1}{2}g \cdot t^2$$

Se chamarmos de $latex t^*$ o instante em que a pedra atinge o solo e levarmos em conta que, nesse instante, a posição (altura) da pedra é zero, teremos:

$$y(t^*)=0=y_0-\frac{1}{2}g \cdot {t^*}^2$$

A equação acima tem duas incógnitas, que são o tempo $latex t^*$ e a altura do penhasco $latex y_0$.

Por outro lado, o tempo $latex t_s$ que o som leva para ir da base ao topo do penhasco é:

$$ t_s= \dfrac{y_0}{V_s}$$

Sabemos também que o tempo decorrido desde o momento em que a pedra foi lançada até que o som do impacto foi ouvido é:

$$T=t^*+t_s=3s \; \Rightarrow \; {t^*}^2=(T-t_s)^2$$

Combinando essas equações, ficamos com:

$$\dfrac{2y_0}{g}=(T-\dfrac{y_0}{V_s})^2$$

Expandindo o quadrado e simplificando, ficamos com a seguinte equação quadrática na variável $latex y_0$, que é apenas a altura do penhasco:

$$\frac{1}{{V_s}^2}{y_0}^2-(\frac{2}{g}+\frac{2T}{V_s})y_0+T^2=0$$

Substituindo os dados conhecidos ficamos com:

$$8,65 \cdot 10^{-6}{y_0}^2 – 0,2217 y_0 +9 =0$$

Resolvendo a equação quadrática, temos que a altura do penhasco é:

$$y_0=40,66m$$