A regra da potência é uma das regras das derivadas mais usadas no Cálculo Diferencial (ou Cálculo I) para derivar uma variável elevada a um expoente numérico. É uma das regras de derivadas mais simples que os alunos aprendem nos primeiros capítulos de Cálculo Diferencial.
Embora seja considerada uma das regras de derivação mais simples, é muito importante aprender como provar essa regra. Portanto, neste artigo focaremos principalmente nas provas da fórmula da regra da potência aplicando os princípios do teorema binomial e da diferenciação logarítmica.
CÁLCULO
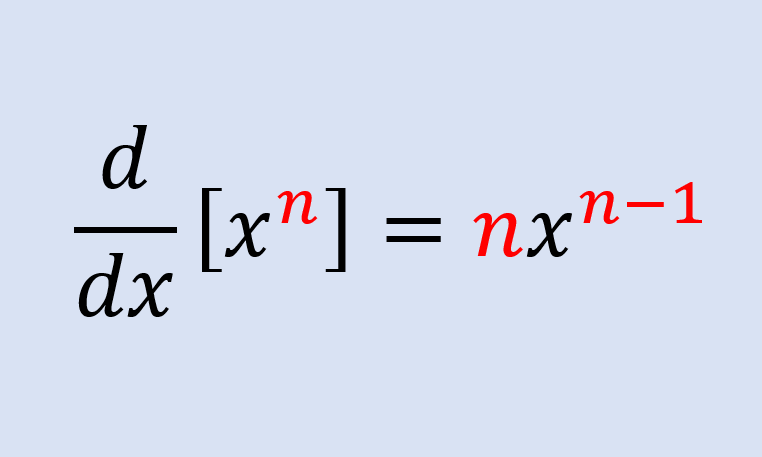
Relevante para…
Aprender a provar a regra da potência com diferentes métodos.
CÁLCULO
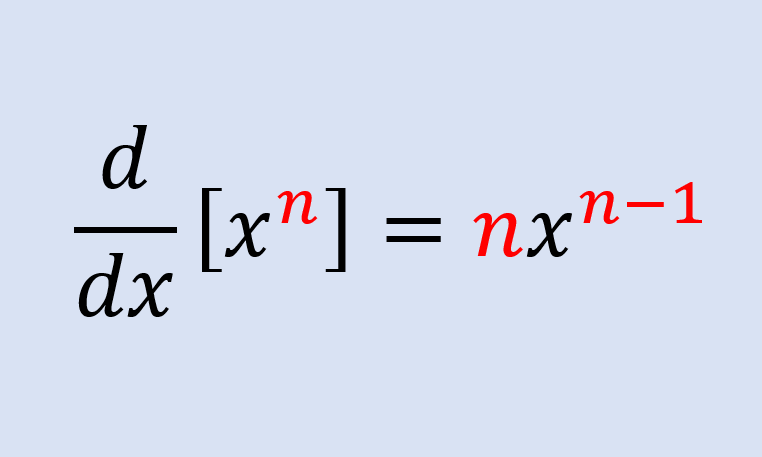
Relevante para…
Aprender a provar a regra da potência com diferentes métodos.
Qual é a regra da potência?
A regra da potência é definida como a derivada de uma variável elevada a um expoente numérico. Essa regra, no entanto, é limitada apenas a variáveis com expoentes numéricos. Portanto, variáveis ou funções elevadas para outra variável ou função não podem usar esta regra.
A regra da potência pode ser usada para derivar qualquer variável elevada a expoentes como nos seguintes casos:
✔️ Elevado a um expoente positivo:
$latex y = x^n$
onde $latex x$ é uma variável e $latex n$ é o expoente numérico positivo
✔️ Elevado a um expoente negativo (função racional na forma exponencial):
$latex y = \frac{1}{x^n}$
$latex y = x^{-n}$
onde $latex x$ é uma variável e $latex n$ é o expoente numérico negativo
✔️ Elevado a um expoente racional (função radical na forma exponencial):
$latex y = \sqrt[n_2]{x^{n_1}}$
$latex y = x^{\frac{n_1}{n_2}}$
onde $latex x$ é uma variável e $latex \frac{n_1}{n_2} = n$ ou o expoente numérico racional $latex n$
E a regra da potência não pode ser usada para derivar:
❌ Elevado a um expoente variável:
$latex y = x^x$
❌ Elevado a qualquer tipo de função:
$latex y = x^{f(x)}$
Mas como exatamente derivamos essas funções dadas usando a regra da potência?
A regra da potência pode ser escrita da seguinte forma:
| $latex f'(x^n) = nx^{n-1}$ |
onde
- $latex x$ é a variável
- $latex n$ é o valor do expoente numérico da variável $latex x$
Em funções polinomiais, a regra da potência também é usada para cada termo e depende inteiramente da soma/diferença das derivadas.
Em casos especiais de funções transcendentais elevadas a um expoente numérico, a regra da potência é apoiada pela fórmula da regra da cadeia, usando a regra da potência como a derivada da função exterior f da função composta $latex f (g(x))$.
Prova da regra da potência usando o teorema binomial
Para entender melhor a prova da regra da potência usando o teorema binomial, é recomendável que você esteja familiarizado com os tópicos O teorema binomial, A inclinação de uma reta tangente e Derivadas por limites.
Podemos lembrar que
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} \left( {\frac{f(x+h)-f(x)}{h}} \right)$$
Aplicando limites, podemos derivar uma função f(x). Mas e se $latex f(x) = x^n$? Se for esse o caso, temos
$$ \frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( {\frac{(x+h)^n – x^n}{h}} \right)$$
Podemos calcular $latex (x+h)^n$ aplicando o teorema binomial. Antes de aplicá-lo ao nosso limite, podemos lembrar que o teorema binomial é um método algébrico para expandir uma expressão binomial.
O teorema binomial ilustra que para expandir uma quantidade de um binômio elevado a um expoente numérico, temos
$$(a+b)^n = \displaystyle \sum_{k=0}^{n} {n\choose k} a^{n-k} b^k$$
onde
- $latex a$ e $latex b$ podem ser uma variável ou uma constante
- $latex n$ é o expoente do binômio
- $latex k$ é a ordem de potência do polinômio na soma.
- $latex {n \choose k}= \frac{n!}{k!(n-k)!}$; também chamado de combinatória $latex n$ escolhe $latex k$ ou $latex {}_n C_k$
Expandindo a soma, temos
$$(a+b)^n = {n\choose 0} a^{n-0} b^0 + {n \choose 1} a^{n-1} b^{1}+ …… + {n \choose n-1} a^{n-(n-1)} b^{n-1} + {n\choose n} a^{n-n} b^{n}$$
$$(a+b)^n = \left(\frac{n!}{0! (n-0)!} \right) \cdot a^n + \left(\frac{n!}{1! (n-1)!} \right) \cdot a^{n-1} b+ …… + \left(\frac{n!}{(n-1)! (n-(n-1))!} \right) \cdot a^1 b^{n-1}+ \left(\frac{n!}{n! (n-n)!} \right) \cdot a^0 b^{n}$$
$$(a+b)^n = a^n + na^{n-1} b + …… + nab^{n-1} + b^{n}$$
Aplicando o teorema binomial sobre $latex (x+h)^n$, temos
$$(x+h)^n = x^n + nx^{n-1} h + …… + nxh^{n-1} + h^n$$
Substituindo isso em nossa equação limite, temos
$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( {\frac{x^n + nx^{n-1} h + …… + nxh^{n-1} + h^n – x^n}{h}} \right)$$
Simplificando um pouco o numerador, já que existem termos semelhantes que podem ser subtraídos, temos
$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( {\frac{nx^{n-1} h + …… + nxh^{n-1} + h^n}{h}} \right)$$
Mas como podemos remover o denominador $latex h$ para evitar um resultado indefinido? Observe que todos os termos do numerador são multiplicados por pelo menos $latex h$ e seu menor denominador comum é $latex h$. Portanto, podemos dividir cada termo por $latex h$:
$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( { \left(\frac{nx^{n-1} h}{h} \right)+ …… + \left( \frac{nxh^{n-1} + h^n}{h} \right) } \right)$$
$$ \frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( nx^{n-1} h^{1-1}+ …… + nxh^{(n-1)-1} + h^{n-1} \right)$$
$$\frac{d}{dx} (x^n) = \lim \limits_{h \to 0} \left( nx^{n-1}+ …… + nxh^{n} + h^{n-1} \right)$$
Avaliando nossos limites pelo método de substituição, temos
$$\frac{d}{dx} (x^n) = nx^{n-1}+ …… + nx(0)^{n} + (0)^{n-1} $$
Sabemos que zero elevado a qualquer expoente exceto 0 e $latex \infty$ é igual a zero, então temos
| $latex f'(x^n) = nx^{n-1}$ |
que agora é a fórmula para a regra da potência.
Prova da regra da potência usando diferenciação logarítmica
Este é realmente o método mais curto para provar a fórmula da regra da potência. No entanto, para entender melhor essa prova, é recomendável que você esteja familiarizado com o tópico Diferenciação Logarítmica, como pré-requisito.
Podemos lembrar que a diferenciação logarítmica consiste em converter ambos os lados da equação em um logaritmo. Isso é usado, na maioria das vezes, em conjunto com a diferenciação implícita.
Por exemplo, suponha que temos a equação:
$latex y = x^n$
que, sendo derivado, é igual a
$latex y’ = f'(x^n)$
Mas como podemos derivar isso supondo que ainda não conhecemos a fórmula da regra da potência?
Avaliando $latex y = x^n$ logaritmicamente para remover o expoente $latex n$, temos
$latex \ln{(y)} = \ln{(x^n)}$
Aplicando propriedades logarítmicas, temos
$latex \ln{(y)} = n \ln{(x)}$
Para derivar, podemos usar a diferenciação logarítmica em ambos os lados da equação:
$latex \frac{d}{dx} (\ln{(y)}) = \frac{d}{dx} (n \ln{(x)})$
Como o expoente $latex n$ deve ser limitado apenas a números reais, trataremos $latex n$ como um coeficiente. Portanto, temos
$latex \frac{d}{dx} (\ln{(y)}) = n \frac{d}{dx} (\ln{(x)})$
Então, aplicando a diferenciação logarítmica, temos:
$latex \frac{y’}{y} = \frac{n}{x}$
Igualando a equação em termos de $latex y’$ ou $latex f'(x^n)$, temos
$latex f'(x^n) = \frac{ny}{x}$
Sabemos que, $latex y = x^n$, então substituímos $latex y$ na equação derivada:
$latex f'(x^n) = \frac{n(x^n)}{x}$
Aplicando as leis dos expoentes, temos
$latex f'(x^n) = nx^n \cdot x^{-1}$
| $latex f'(x^n) = nx^{n-1}$ |
que agora é a fórmula para a regra da potência.
Veja também
Interessado em aprender mais sobre a regra da potência? Dê uma olhada nessas páginas:



