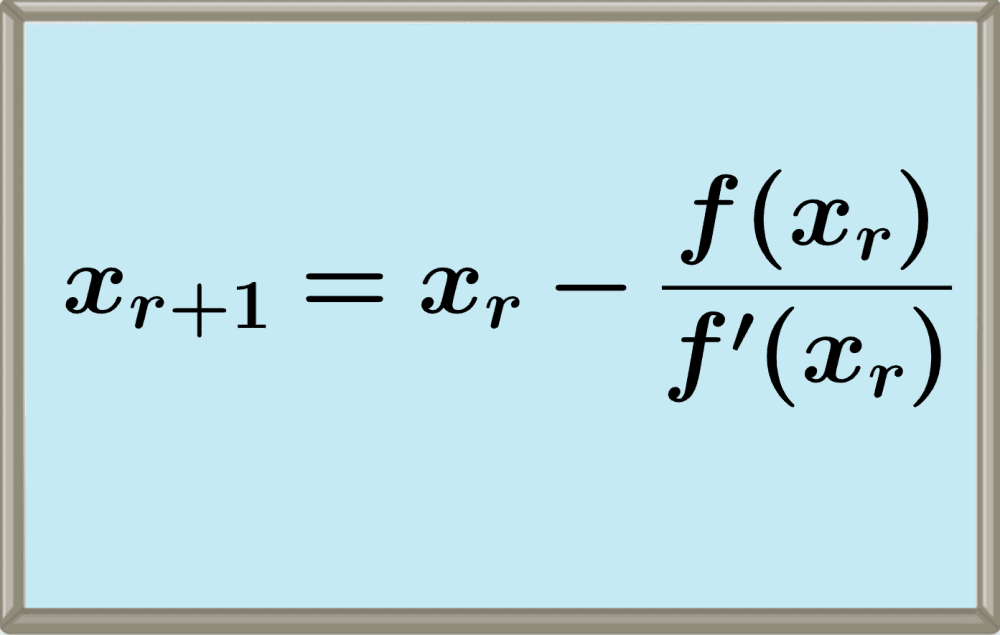O método Newton-Raphson é um algoritmo utilizado para encontrar as raízes de uma função. É um método iterativo que utiliza a derivada da função para melhorar a precisão da estimativa da raiz em cada iteração.
Neste artigo, vamos analisar uma breve introdução ao método Newton-Raphson, incluindo os seus passos e vantagens. Daremos também exemplos da utilização do método para encontrar a raiz de uma função.
Passos para a aplicação do método Newton-Raphson
O método Newton-Raphson é um algoritmo iterativo para encontrar as raízes de uma função. Para utilizar o método, siga estes passos:
1. Escolha um valor inicial para x.
Este valor é uma estimativa onde se espera que haja uma raiz.
2. Encontrar o valor da função utilizando o valor de x do passo 1.
3. Encontrar o valor da derivada da função utilizando o valor de x do passo 1.
4. Use os valores encontrados para actualizar a estimativa de raiz usando a seguinte fórmula:
$$x_{r+1}=x_{r}-\frac{f(x_r)}{f^{\prime}(x_r)}$$
5. Repetir os passos 2-4 até a estimativa da raiz convergir para um valor preciso.
Vantagens e desvantagens do método Newton-Raphson
Uma das principais vantagens do método Newton-Raphson é que pode convergir rapidamente para a raiz de uma função, muitas vezes em algumas iterações.
Além disso, o método pode lidar com funções de qualquer complexidade, incluindo funções não lineares. Isto torna-o um algoritmo eficiente para encontrar raízes de funções complexas.
Outra vantagem do método Newton-Raphson é que utiliza a derivada da função para se aproximar da raiz, o que pode fornecer uma estimativa mais precisa da raiz em comparação com outros métodos que não utilizam derivadas.
No entanto, o método Newton-Raphson também tem alguns inconvenientes. Um dos principais inconvenientes é que o método pode não convergir se a estimativa inicial estiver demasiado longe da verdadeira raiz.
Além disso, o método pode convergir para um mínimo ou máximo local e não para um mínimo ou máximo global, o que pode levar a uma estimativa incorreta da raiz.
Finalmente, o método requer o cálculo de derivadas, o que pode ser difícil para algumas funções.
Método Newton-Raphson – Exemplos com respostas
EXERCÍCIO 1
Usar o método Newton-Raphson para encontrar uma raiz negativa do seguinte polinômio cúbico:
$$x^3-2x+1$$
Utilizar como ponto de partida o valor $latex x_0=-1,5$ para encontrar por aproximações sucessivas o valor da raiz com três casas decimais de precisão.
Solução
Seguimos estes passos para aplicar o método Newton-Raphson:
1) Definir a função, neste exemplo, temos: $latex f(x)=x^2-2x+1$
2) Encontrar a derivada desta função: $latex f^{\prime}(x)= 3x^2-2$
3) Escolha o ponto de partida, no nosso exemplo este valor é considerado se segue: $latex x_{0}=-1,5 $
4) Avalie a função e a sua derivada em x₀: $latex f(x_{0})= 0,625$; $latex ~f^{\prime}(x_{0})= 4,75$
5) Aplicar a fórmula iterativa de Newton-Raphson para encontrar uma primeira estimativa:
$$ x_{1}=x_{0}-\frac{f(x_{0})}{f^{\prime}(x_{0})}$$
$$x_{1}= -1, 6316 $$
6) Repetir os passos 4) e 5) até a estimativa corresponder ao número desejado de casas decimais:
$latex f(x_{1})= -8,0187×10^{-2}~~$ $latex ~~ f^{\prime}(x_{1})= 5, 9861$
$$ x_{2}=x_{1}-\frac{f(x_{1})}{f^{\prime}(x_{1})}~~~~ x_{2}= -1, 6182 $$
$latex f(x_{2})= -8, 7589×10^{-4} ~~$ $latex ~~ f^{\prime}(x_{2})= 5, 8556$
$$ x_{3}=x_{2}-\frac{f(x_{2})}{f^{\prime}(x_{2})}~~~~ x_{3}= -1, 618$$
7) Neste exemplo, só foi necessário fazer 3 iterações, uma vez que as três casas decimais foram repetidas entre a segunda e a terceira iteração.
O valor para a raiz é tomado como o valor da última iteração: Solução: $latex x=-1,618$.
EXERCÍCIO 2
Encontrar nas três casas decimais mais próximas o valor de x que satisfaz a seguinte equação:
$$ln(x)=2$$
Solução
A função cujos zeros (ou raízes) devem ser encontrados é definida. A sua derivada é também calculada.
$$f(x)=ln(x)-2$$
$$ f^{\prime}(x)= \frac{1}{x} $$
A função é analisada para obter um valor inicial. Por exemplo, note-se que $latex f(7)=-0,054$ e $latex f(8)=+0,079$, o que nos diz que a raiz está entre 7 e 8.
Tomaremos como valor inicial 8, $latex x_{0}=8$:
$latex f(x_{0})= 7,9442×10^{-2}~~$ $latex ~~ f^{\prime}(x_{0})= 0,125$
$$ x_{1}=x_{0}-\frac{f(x_{0}}{f^{\prime}(x_{0})} ~~~~ x_{1}= 7, 3645$$
$latex f(x_{1})= -3, 3332×10^{-3}~~$ $latex ~~ f^{\prime}(x_{1})= 0,13579$
$$ x_{2}=x_{1}-\frac{f(x_{1}}{f^{\prime}(x_{1})} ~~~~ x_{2}= 7, 389$$
$latex f(x_{2})= -5, 5429×10^{-6}~~$ $latex ~~ f^{\prime}(x_{2})= 0,13534$
$$ x_{3}=x_{2}-\frac{f(x_{2}}{f^{\prime}(x_{2})} ~~~~ x_{3}= 7, 3891$$
Concluímos que a solução da equação ln(x)=2 é x=7,389 para as três casas decimais mais próximas.
EXERCÍCIO 3
Encontrar o valor de x que satisfaz a seguinte equação:
$$ x^x = 5 $$
Solução
A equação dada é equivalente a:
$$ x^x – 5 = 0 $$
Definimos a função f: $latex f(x)= x^x – 5 $
Uma vez que se trata de uma equação não linear, é necessário encontrar a solução através de um método numérico, tal como o método de Newton-Raphson.
Para aplicar este método, é necessário calcular a derivada da função f(x), que chamaremos f‘(x):
$$ f'(x) = x^x (ln(x) +1) $$
Se $latex x_i $ é um valor próximo da raiz, um valor ainda mais próximo é: $latex x_{i+1} = x_i – \frac{f(x_i)}{f'(x_i)}$.
Se repetirmos o processo com o novo valor obtido, teremos um valor ainda mais próximo da raiz. Se repetirmos sucessivamente, podemos ter uma solução precisa.
Neste exemplo, tomaremos como ponto de partida o valor $latex x_0 = 2$ e como mostra a tabela seguinte, com apenas quatro iterações o valor de x é encontrado, com uma precisão de 6 casas decimais:
| $latex i$ | $latex x_{i}$ | $latex f(x_{i})$ |
| 0 | 2 | -1 |
| 1 | 2,1476540273 | 0,1635039111 |
| 2 | 2,1297070022 | 0,0029377859 |
| 3 | 2,1293725959 | 0,0000009937 |
| 4 | 2,1293724828 | 0 |
$latex |x_{4}-x_{3}|=0,0000001131$
EXERCÍCIO 4
Interpretar geometricamente o significado da fórmula para o método Newton-Raphson:
$$ x_{i+1} = x_i – \frac{f(x_i)}{f'(x_i)}$$
Solução
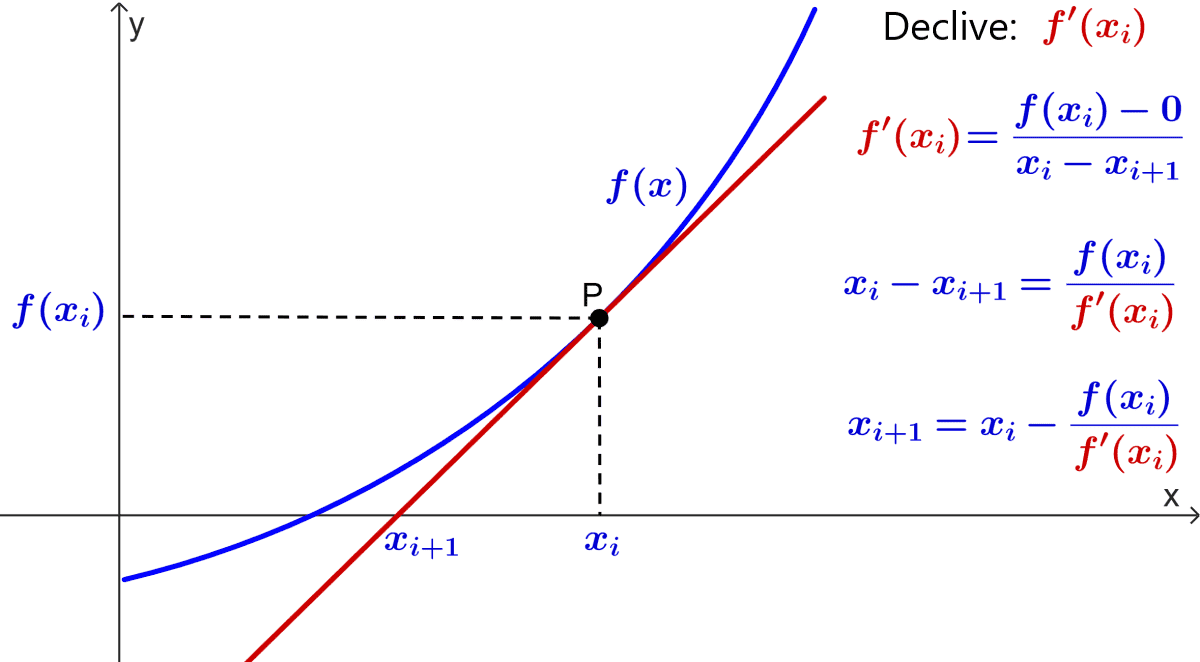
A interpretação geométrica é a seguinte:
No gráfico da função $latex y=f(x)$, toma-se o valor $latex x=x_i$, e obtém-se seu correspondente valor $latex y_i = f(x_i)$. Isso representa um ponto P de coordenadas $latex (x_i, f(x_i))$ na curva da função $latex f(x)$.
Se a reta tangente à curva for traçada através desse ponto, então essa reta intersecta o eixo x no ponto $latex x_{i+1}$.
Lembrando que o declive da reta tangente à curva da função $latex f(x)$ é sua derivada $latex f'(x)$, então o declive da tangente no ponto P é $latex f'( x_i)$.
Mas o declive é também a tangente do ângulo de inclinação da reta no ponto de intersecção com o eixo x, calculado da seguinte forma:
$$ f'(x_i) = \frac{f(x_i)-0}{x_i – x_{i+1}}$$
Se isolarmos $latex x_{i+1} $ da equação acima, então obtemos a fórmula para o método de Newton-Raphson:
$$ x_{i+1} = x_i – \frac{f(x_i)}{f'(x_i)}$$
EXERCÍCIO 5
Encontre as soluções para a seguinte equação:
$$ cos(x) = x^2 $$
Solução
1.- Esta é uma equação não-linear que não tem uma solução analítica exata.
2.- Definimos a função $latex f(x) = cos(x) – x^2 $. Os zeros desta função são os valores de x que satisfazem $latex f(x)=0$ e são as soluções para a equação original.
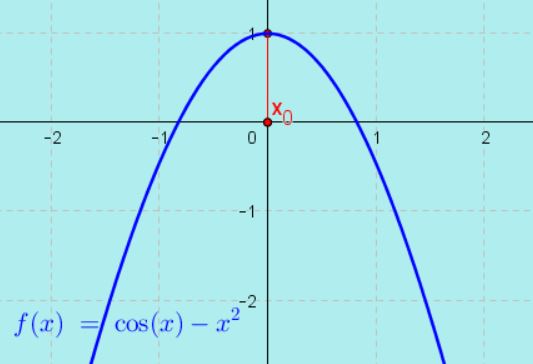
3.- Esboçando um gráfico da função $latex f(x)$, temos:
4.- Pelo gráfico, vemos que a função tem duas raízes, uma próxima do valor x=-1 e a outra do valor x=+1.
5.- Para determinar com mais precisão o valor das raízes da função f(x), utiliza-se o método de Newton-Raphson. Este método requer a derivada de $latex f^{\prime}(x)$, a qual é $latex f^{\prime}(x) = -\sin(x)-2x$.
6.- O método também requer que seja fornecido um valor inicial x0, tal que $latex f'(x_0) \neq 0$ e que seja o mais próximo possível do valor verdadeiro da raiz.
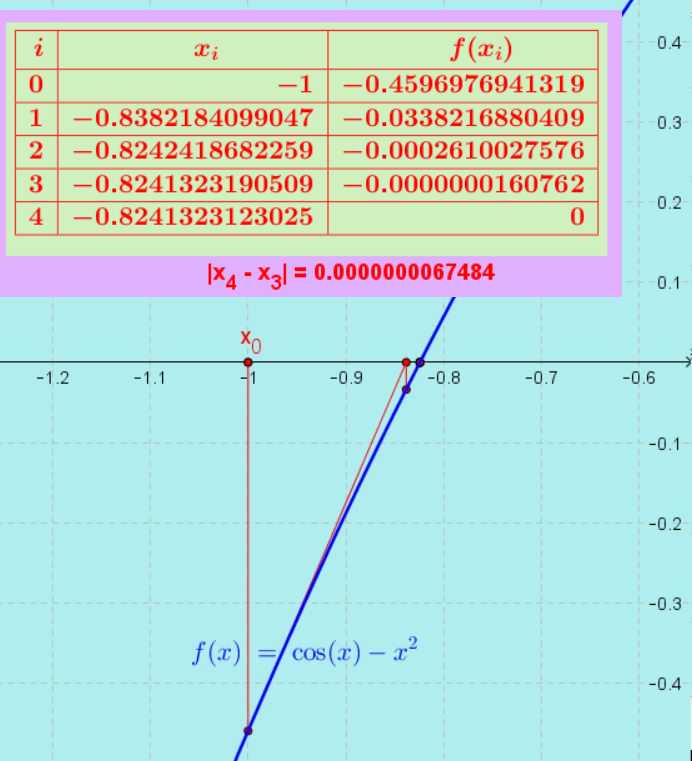
7.- Para encontrar a primeira raiz, tomamos como ponto de partida x0 = -1. Aplicamos recursivamente a fórmula do método, partindo de i=0 até i=4. Os resultados são mostrados abaixo:
O valor da primeira raiz é: $latex x_{r1} = -0,824132312$ onde as primeiras oito casas decimais são exatas e a nona é estimada.
8.- Se $latex x_{0} = +1$ é tomado como ponto de partida, o método Newton-Raphson, após quatro iterações, dá a segunda raiz: $latex x_{r2} = +0,824132312$, um resultado que poderia ter sido esperado devido à simetria da função f(x).
EXERCÍCIO 6
Find the roots of the function:
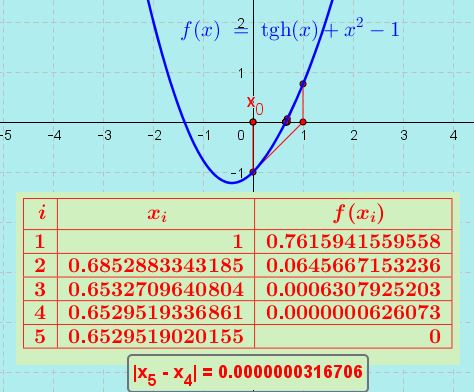
$$ tgh(x) + x^2 -1$$
Solução
É conveniente traçar o gráfico da função para se ter uma ideia da localização das raízes. Uma das raízes é positiva (perto de +0,5) e a outra é negativa (perto de -1,5).
O método Newton-Raphson requer o cálculo da derivada de f(x):
$$ f'(x) = 1 – tgh^2(x) +2x $$
Começando com o valor inicial $latex x_{0} = 0$, em cinco iterações da fórmula $latex x_{i+1} = x_i – \frac{f(x_i)}{f'(x_i)}$, o valor da raiz positiva é obtido com oito casas decimais de precisão:
A raiz positiva da função dada é: 0,65295190.
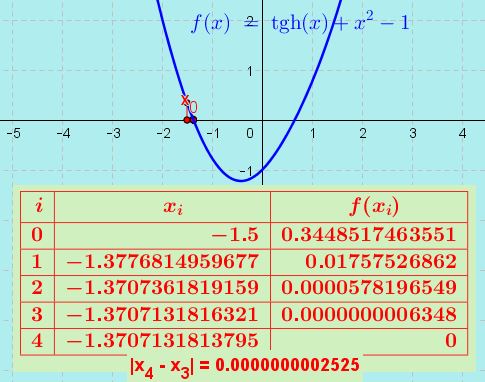
Para obter a raiz negativa, partimos de um valor próximo do mesmo, $latex x_{0}=-1,5$.
A raiz negativa da função dada é: -1,3707713181, com uma precisão de dez casas decimais.
EXERCÍCIO 7
Resolver a seguinte equação usando o método de Newton-Raphson:
$$ e^x = 2 – x^2 $$
com um mínimo de quatro casas decimais.
Solução
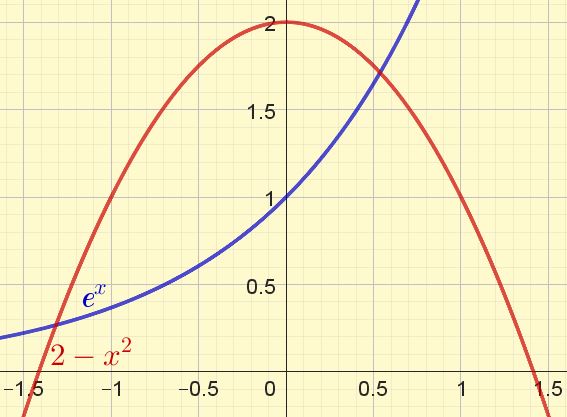
1.- Começamos por esboçar o gráfico de $latex e^x$ e $latex 2-x^2$. Os pontos de intercepção em x são as soluções gráficas para o problema.
Existem dois intercepção x, que correspondem às soluções da equação dada. Um deles tem um valor de coordenada x próximo de -1,5 e o outro, um valor de coordenada x próximo de +0,5.
3.- Para aplicar o método Newton-Rapson, definimos a função:
$$ f(x) = e^{x} -2 + x^2 $$
os valores onde $latex f(x)=0$ serão as soluções para a equação dada.
4.- Encontrar a derivada de f(x):
$$ f'(x) = e^{x} + 2x $$
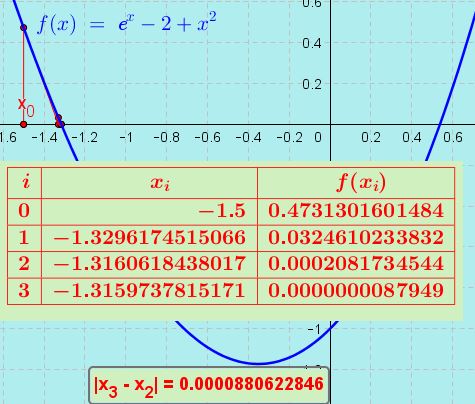
5.- Para encontrar a primeira raiz de f(x), tomamos como ponto de partida do método o valor $latex x_{0}=-1,5$.
6.- Aplicamos a fórmula de Newton Raphson sucessivamente até se atingir a precisão desejada:
$latex x_{i+1} = x_i – \frac{f(x_i)}{f'(x_i)}$, começando com o valor inicial, $latex x_{0}$ para obter $latex x_{1}$. Então com $latex x_{1}$ para obter $latex x_{2}$. É repetido até que a diferença entre o último valor menos o anterior tenha um valor absoluto menor ou igual a 0,00001
Os resultados numéricos são mostrados abaixo:
obter o valor da primeira solução: x=-1,31597
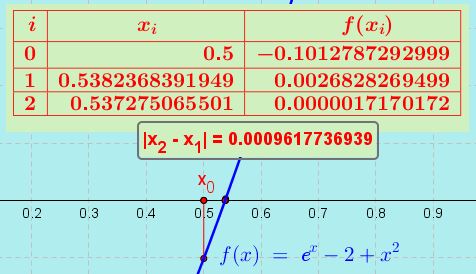
8.- A segunda solução da equação está próxima de +0,5, pelo que será utilizada como valor inicial para obter a solução com a precisão requerida de pelo menos quatro casas decimais.
9.- Uma vez que começamos com um valor bastante próximo da raiz exata, obtivemos um resultado com uma precisão de três casas decimais em apenas duas iterações:
A segunda solução para a equação dada é: x=+0,53727
EXERCÍCIO 8
Utilizar o método Newton-Raphson para obter uma aproximação de pelo menos três casas decimais exatas:
$$ \sqrt[6]2$$
Solução
A equação a resolver é $latex \sqrt[6]2 =x $ que é equivalente a:
$latex x^6 -2 =0$ con x>0.
Então, definimos $latex f(x) = x^6-2$ cuja derivada é $latex f^{\prime}(x)=6x^5 $.
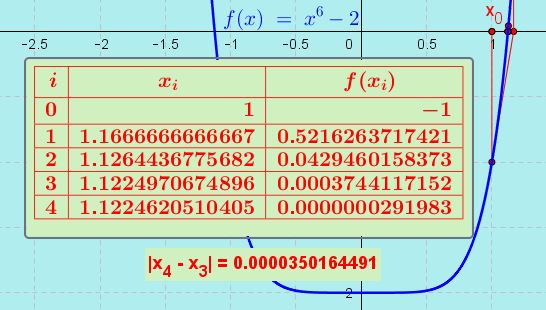
Aplicando iterativamente a fórmula para o método de Newton-Raphson $latex x_{i+1} = x_i – \frac{f(x_i)}{f'(x_i)}$ e partindo de $latex x_{0}=1$, obtemos:
Portanto:
$$ \sqrt[6]2=1,12246$$
EXERCÍCIO 9
Encontrar um valor aproximado com pelo menos três casas decimais para:
$$\sqrt {\sqrt 2}$$
Solução
A equação a resolver é $latex \sqrt[4]2 =x $ que é equivalente a:
$latex x^4 -2 =0$ com x>0.
Então, definimos $latex f(x) = x^4-2$ cuja derivada é $latex f'(x)=4x^3 $.
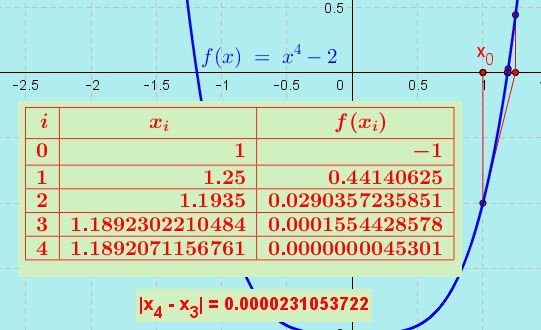
Aplicando iterativamente a fórmula para o método de Newton-Raphson $latex x_{i+1} = x_i – \frac{f(x_i)}{f'(x_i)}$ e partindo de $latex x_{0}=1$, obtemos:
Portanto:
$$\sqrt {\sqrt 2}= 1,18920$$
EXERCÍCIO 10
Utilizar o método Newton-Raphson para encontrar uma aproximação decimal:
$$ln(13)$$
Solução
A equação a ser resolvida é: $latex ln(13)=x $
Tomando a função exponencial com base e em ambos os lados, temos $latex e^x=13 $.
Agora, definimos a função $latex f(x)= e^x – 13$.
A derivada de f é: $latex f'(x)=e^x$.
Iniciamos o processo iterativo com a fórmula $latex x_{i+1} = x_i – \frac{f(x_i)}{f'(x_i)}$, com o valor inicial $latex x_{0} = 2$, obtendo os seguintes valores:
Como resultado final, temos:
$$ln(13) = 2,5649$$
Método Newton-Raphson – Problemas de prática
Use o método Newton Raphson para encontrar a raiz de $latex x\ln (x)=2$ que fica entre $latex x=2$ e $latex x=3$.
Escreva a resposta com três casas decimais.
Veja também
Interessado em aprender mais sobre métodos numéricos? Pode visitar estas páginas: