A transformação de funções são as mudanças que podemos aplicar a uma função para modificar seu gráfico. Uma das transformações importantes é o reflexo das funções. Uma função pode ser refletida em torno do eixo x quando temos –f(x) e pode ser refletida em torno do eixo y quando temos f(-x).
A seguir, aprenderemos como obter uma reflexão de uma função, tanto no eixo x quanto no eixo y. Usaremos exemplos para ilustrar as ideias importantes.
ÁLGEBRA
Relevante para…
Aprender sobre a reflexão de funções no eixo x e no eixo y.
ÁLGEBRA
Relevante para…
Aprender sobre a reflexão de funções no eixo x e no eixo y.
Realizar reflexões de uma função sobre o eixo x e o eixo y
As reflexões de uma função são transformações que conseguem que o gráfico da função se reflita com respeito a um dos eixos. Uma reflexão equivale a “inverter” o gráfico da função usando os eixos como referências.
Podemos entender este conceito usando a função $latex f(x)=x+1$. Quando traçamos o gráfico dessa função, obtemos a reta mostrada no gráfico a seguir:
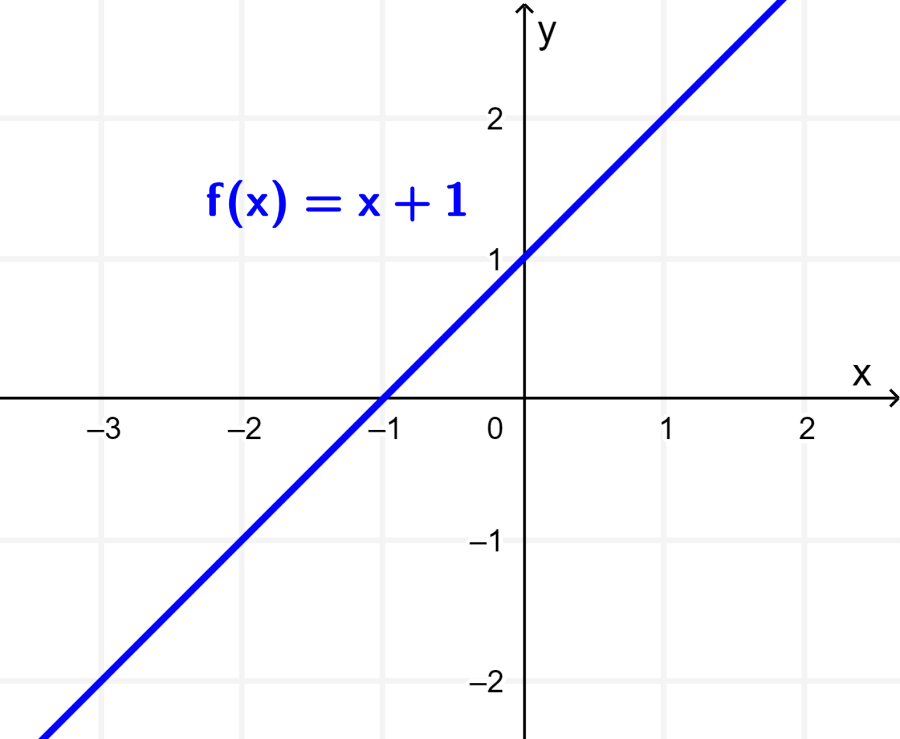
Agora, podemos realizar duas transformações diferentes na função $latex f(x)$ para obter as seguintes funções:
(i) $latex -f(x)=-(x+1)=-x-1$
(ii) $latex f(-x)=(-x)+1=-x+1$
Se plotarmos as funções (i) e (ii) com a função original $latex f(x)$, teremos:
No caso (i), o gráfico da função original $latex f(x)$ foi refletido em relação ao eixo x.
No caso (ii), o gráfico da função original $latex f(x)$ foi refletido em relação ao eixo y.
Resumindo, temos:
- A transformação $latex -f(x)$, resulta em uma reflexão do gráfico de $latex f(x)$ sobre ao eixo x.
- A transformação $latex f(-x)$ resulta em uma reflexão do gráfico de $latex f(x)$ sobre o eixo y.
Exemplos de reflexão de funções
Nos exemplos a seguir, aplicamos o que aprendemos sobre reflexão de funções sobre o eixo x e sobre o eixo y. Cada exemplo tem uma solução detalhada.
EXEMPLO 1
Faça o gráfico da função $latex f(x)=x^2-2$ e, em seguida, faça o gráfico da função $latex g(x)=-f(x)$.
Solução
O gráfico de f é uma parábola transladada 2 unidades para baixo, como mostrado no gráfico abaixo:
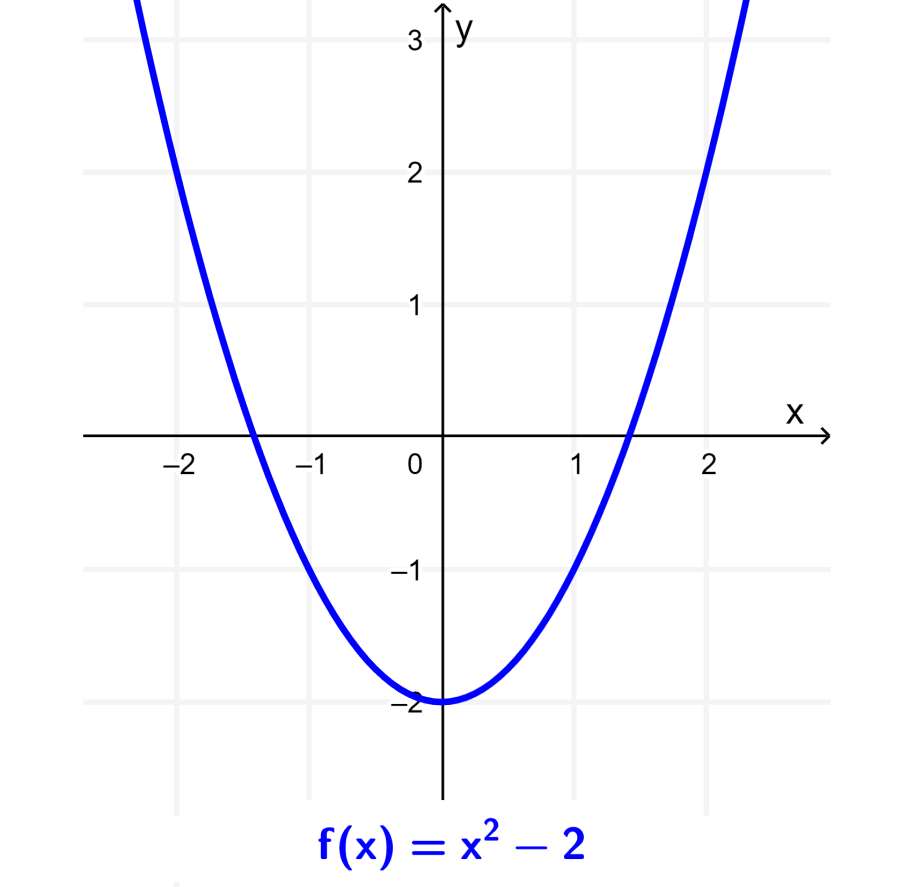
Agora, quando aplicamos a transformação na função g, obtemos $latex g(x)=-x^2+2$. Podemos obter seu gráfico refletindo o gráfico de f em torno do eixo x:
.
EXEMPLO 2
Qual é a diferença entre o gráfico de $latex f(x)=\cos(2x)$ e o gráfico de $latex g(x)=\cos(-2x)$?
Solução
O gráfico da função $latex f(x)=\cos(2x)$ é o seguinte:
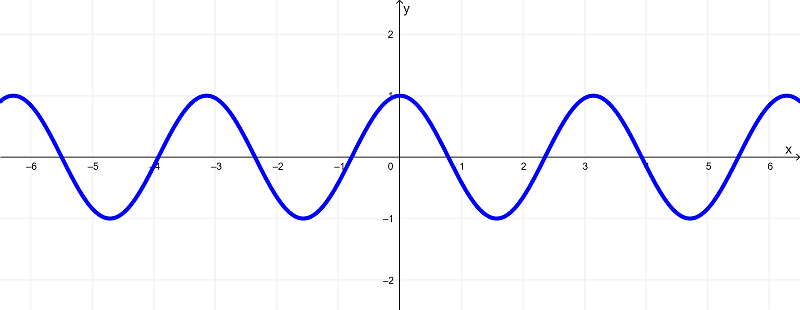
Podemos ver que a função g é equivalente a $latex g(x)=f(-x)$. Então, a função g é obtida aplicando uma reflexão sobre o eixo y.
Agora, podemos ver que o gráfico de $latex f(x)=\cos(2x)$ tem simetria em relação ao eixo y. Isso significa que, se refletirmos sobre o eixo y, obteremos o mesmo gráfico.
Portanto, os gráficos de $latex f(x)=\cos(2x)$ e $latex g(x)=\cos(-2x)$ são os mesmos.
EXEMPLO 3
Faça o gráfico da função de valor absoluto na forma básica e, em seguida, faça o gráfico de $latex g(x)=-|x|$.
Solução
O gráfico da função de valor absoluto em sua forma básica, $latex f(x)=|x|$, é o seguinte:
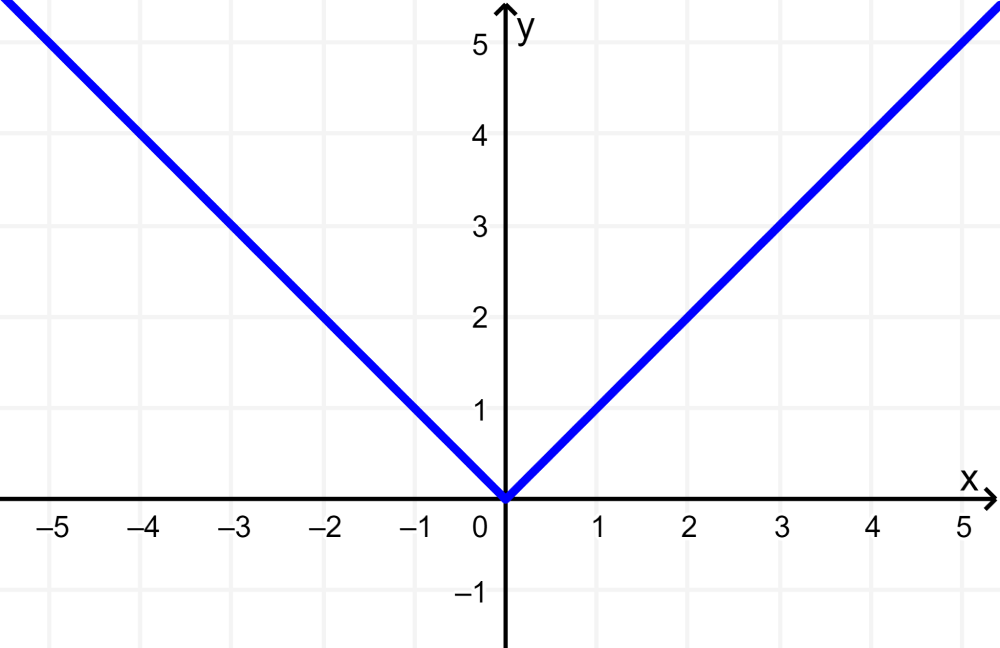
Agora, podemos ver que a função g é igual a $latex g(x)=-f(x)$. Assim, obtemos o gráfico de g aplicando uma reflexão sobre o eixo x ao gráfico de f.
.
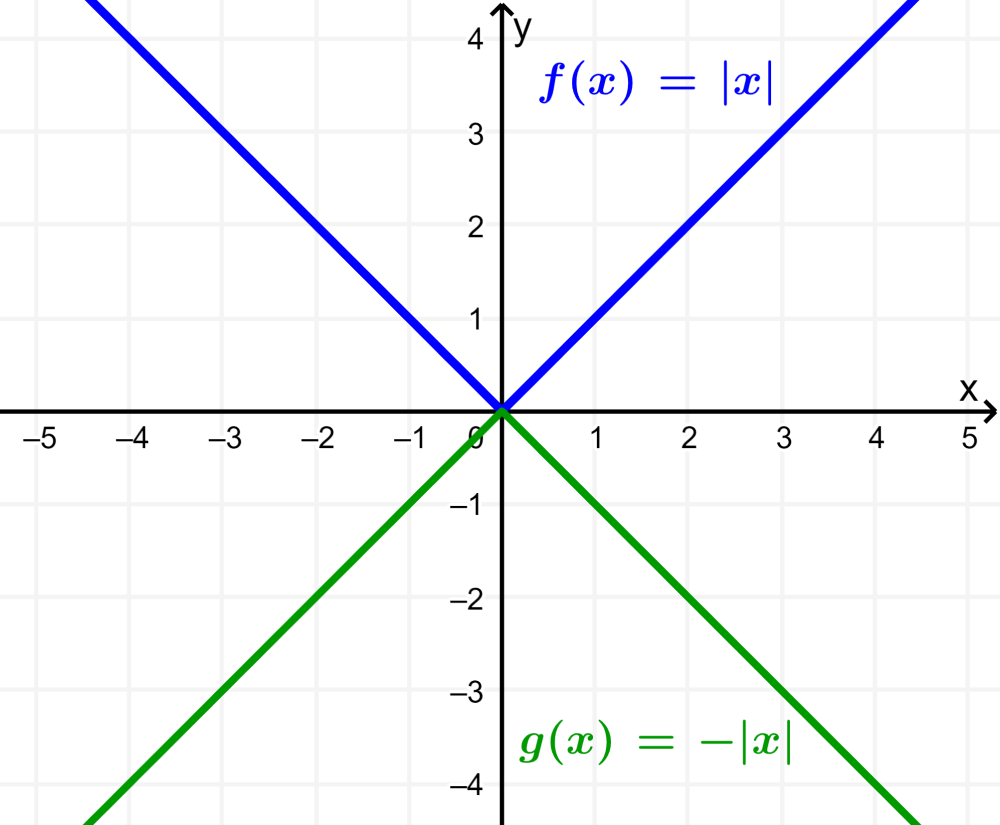
EXEMPLO 4
O que é uma função que reflete sobre o eixo y da função $latex f(x)=3x^2+5x+3$?
Solução
Para obter uma reflexão sobre o eixo y, temos que aplicar a transformação $latex g(x)=f(-x)$.
Assim, podemos encontrar a função g substituindo –x por x na função f:
$latex g(x)=3(-x)^2+5(-x)+3$
$latex g(x)=3x^2-5-x+3$
Exercícios de reflexão de funções para resolver
Resolva os exercícios a seguir usando tudo o que você aprendeu sobre reflexão de funções.
Veja também
Interessado em aprender mais sobre transformações de funções? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
