O número de raízes em um polinômio é igual ao grau desse polinômio. Por exemplo, em polinômios quadráticos, sempre teremos duas raízes contadas por multiplicidade. Essas raízes podem ser reais ou complexas, dependendo do determinante da equação quadrática.
A seguir, aprenderemos sobre o Teorema Fundamental da Álgebra e o Teorema das Raízes Conjugadas. Usaremos esses teoremas para aprender sobre as raízes complexas de um polinômio. Além disso, veremos alguns exemplos para aprender como obter as raízes complexas de um polinômio quadrático usando a fórmula de Bhaskara.
Como saber quantas raízes complexas um polinômio possui?
Para determinar quantas raízes complexas um polinômio possui, temos que usar o teorema fundamental da álgebra. Este teorema nos diz que:
Teorema fundamental da álgebra
Um polinômio $latex p(x)$ de grau n com coeficientes complexos tem, contado com multiplicidade, exatamente n raízes.
A parte “contado com multiplicidade” significa que devemos contar as raízes pela sua multiplicidade, ou seja, pelas vezes que se repetem. Por exemplo, na equação $latex {{(x-2)}^3}(x+2)=0$, temos um polinômio de grau quatro.
No entanto, só podemos contar duas raízes reais. Isso ocorre porque a raiz em $latex x = 2$ é uma raiz múltipla com multiplicidade de três. Portanto, o número total de raízes, ao contar a multiplicidade, é quatro.
Raízes complexas de um polinômio quadrático
Primeiro, vamos começar considerando o teorema das raízes conjugadas:
Teorema das raízes conjugadas
Temos que $latex p(x)$ é um polinômio com coeficientes complexos. Se o número complexo $latex z= a+bi$ é uma raiz do polinômio p, então seu conjugado $latex {{z}^{\ast}}=a-bi$ também é uma raiz.
A partir do teorema fundamental do cálculo, sabemos que qualquer equação quadrática terá duas raízes. E a partir do teorema das raízes conjugadas, sabemos que se o polinômio tiver coeficientes reais e se não tiver raízes reais, então suas raízes serão um par de conjugados complexos.
Se tiver raízes reais, pode ter duas raízes reais diferentes ou uma raiz real repetida. Não é possível ter uma raiz conjugada e uma raiz real. Para distinguir entre esses diferentes casos, temos o conceito de discriminante:
Discriminante
O discriminante de uma equação quadrática $latex a{{x}^2}+bx+c=0$ é definido como $latex {{b}^2}-4ac$. Muitas vezes , $latex \Delta$ é usado para denotar o discriminante.
Usando o discriminante, podemos distinguir os três tipos de casos em equações quadráticas da seguinte forma:
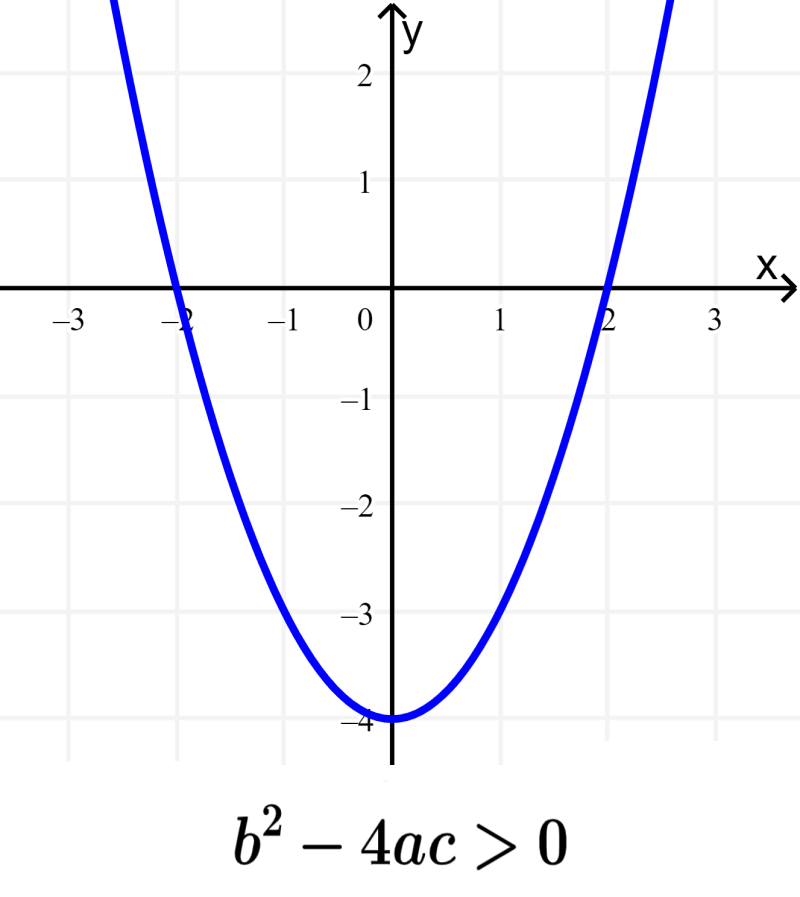
1. Discriminante positivo: $latex {{b}^2}-4ac>0$, duas raízes reais;
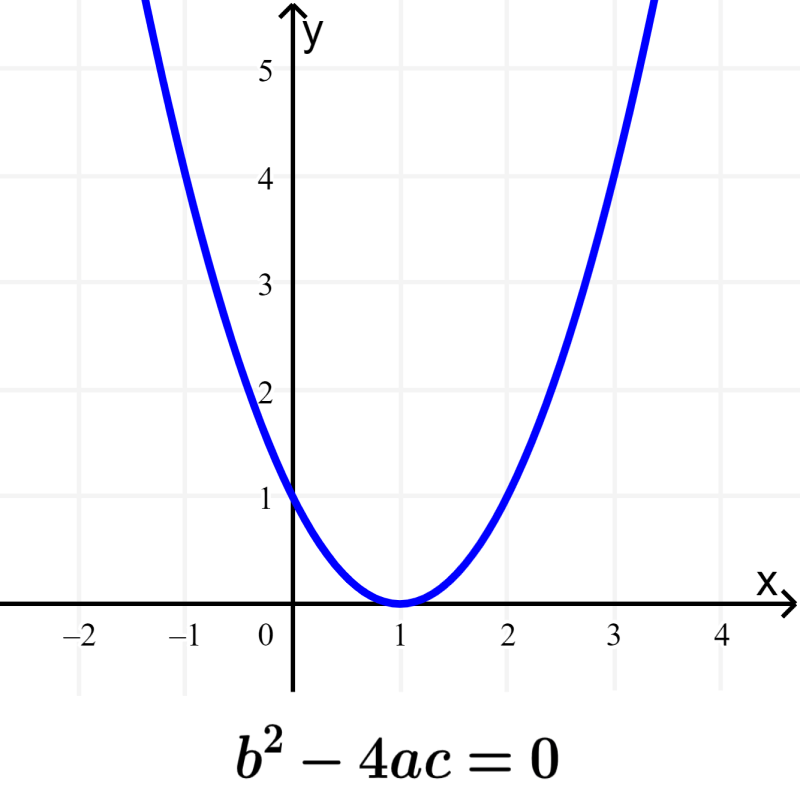
2. Discriminante zero: $latex {{b}^2}-4ac=0$, uma raiz real repetida;
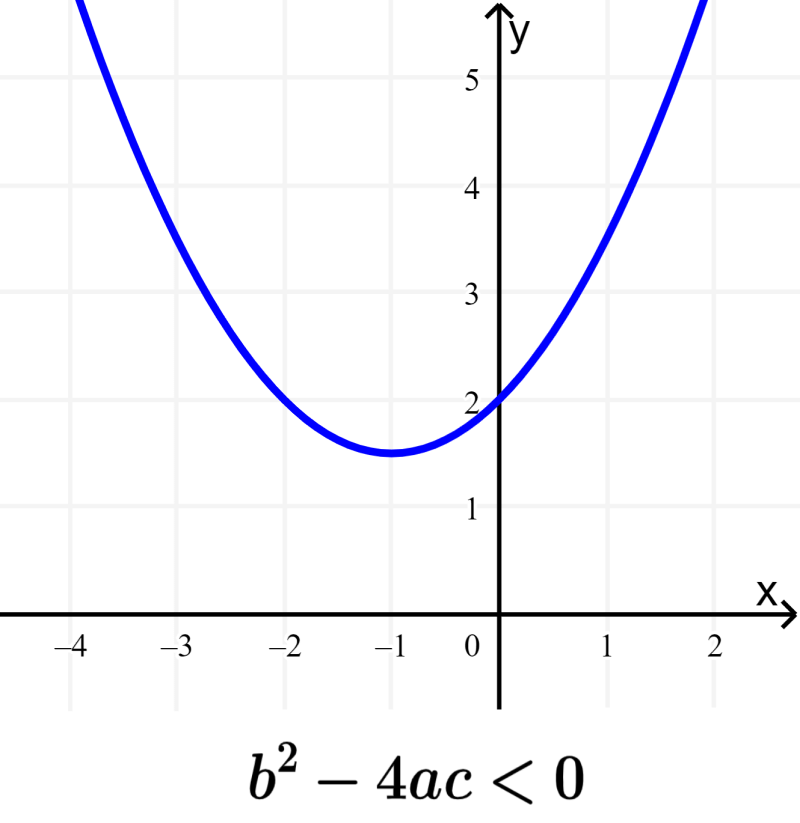
3. Discriminante negativo: $latex {{b}^2}-4ac<0$, raízes conjugadas complexas.
Os gráficos a seguir mostram cada caso:
Portanto, usamos a fórmula quadrática para encontrar as raízes reais ou complexas de um polinômio quadrático:
| $latex x=\frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}$ |
Exercícios resolvidos de raízes complexas de um polinômio
Os exercícios a seguir usam o que você aprendeu sobre o teorema fundamental da álgebra, o teorema das raízes conjugadas e as raízes complexas dos polinômios quadráticos. Tente resolver os exercícios sozinho antes de ver a resposta.
EXERCÍCIO 1
Quantas raízes o polinômio $latex (2{{x}^3}+2x+1)(3{{x}^2} -3)$ tem?
Solução
Usando o teorema fundamental da álgebra, sabemos que o número de raízes é igual ao grau do polinômio. Nesse caso, temos um polinômio na forma fatorada. Para encontrar o grau do polinômio, podemos expandi-lo para encontrar o termo com o maior grau.
Como alternativa, poderíamos economizar um pouco de esforço procurando o termo com o grau mais alto em cada parêntese. O grau do polinômio será o grau do produto desses termos.
Nos primeiros parênteses, o termo de maior grau é $latex 2{{x}^3}$. Nos segundos parênteses, o termo de grau mais alto é $latex 3{{x}^2}$. Portanto, o produto desses dois termos terá um grau 5. Portanto, o polinômio terá 5 raízes.
EXERCÍCIO 2
Determine o tipo de raízes da equação $latex {{x}^2} -2x+3=0$.
Solução
Para determinar o tipo de raízes, temos que usar o determinante $latex {{b}^2}-4ac$. Para esta equação, temos $latex a=1, b=-2$ e $latex c=3$. Então, temos:
$latex {{b}^2}-4ac={{(-2)}^2}-4(1)(3)$
$latex =4-12$
$latex =-8$
Como o discriminante é menor que zero, sabemos que a equação tem duas raízes complexas.
EXERCÍCIO 3
Resolva a equação $latex 5{{x}^2}=-320$.
Solução
Podemos resolver essa equação diretamente, sem usar a fórmula quadrática.
Dividimos ambos os lados por 5 para resolver para $latex {{x}^2}$:
$latex 5{{x}^2}=-320$
$latex {{x}^2}=-64$
Podemos obter a raiz quadrada de ambos os lados, lembrando que podemos obter as raízes positivas e negativas:
$latex x=\pm\sqrt{-64}$
A propriedade dos números complexos nos diz que podemos escrever $latex \sqrt{-a}$ como $latex i\sqrt{a}$. Então, temos:
$latex x=\pm i\sqrt{64}$
$latex =\pm 8i$
EXERCÍCIO 4
Encontre as raízes do polinômio quadrático $latex {{x}^2} -4x+8=0$.
Solução
Usando os valores $latex a=1$, $latex b=-4$ e $latex c=8$ na fórmula de Bhaskara, temos:
$latex x=\frac{{-(-4)\pm \sqrt{{{{{( -4)}}^{2}}-4( 1 )(8)}}}}{{2( 1)}}$
$latex =\frac{{4\pm \sqrt{{16-32}}}}{2}$
$latex =\frac{{4\pm \sqrt{{-16}}}}{2}$
$latex =\frac{4}{2}\pm\frac{\sqrt{{-16}}}{2}$
$latex =2\pm\frac{\sqrt{{-16}}}{2}$
A propriedade dos números complexos nos diz que podemos escrever $latex \sqrt{-a}=i\sqrt{a}$. Então, temos:
$latex x=2\pm\frac{\sqrt{{16}}}{2}i$
$latex =2\pm\frac{4}{2}i$
$latex =2\pm 2i$
Portanto, temos duas soluções para a equação quadrática:
$latex x=2+2i$, $latex x=2-2i$
EXERCÍCIO 5
Encontre as soluções para a equação $latex 3{{x}^2} -4x+10=0$.
Solução
Podemos identificar os valores $latex a=3$, $latex b=-4$ e $latex c=10$ e os usamos na fórmula de Bhaskara:
$latex x=\frac{{-(-4)\pm \sqrt{{{{{( -4)}}^{2}}-4( 3 )(10)}}}}{{2( 3)}}$
$latex =\frac{{4\pm \sqrt{{16-120}}}}{6}$
$latex =\frac{{4\pm \sqrt{{-104}}}}{6}$
$latex =\frac{{4\pm \sqrt{{-4}}\sqrt{{26}}}}{6}$
$latex =\frac{{4\pm 2i\sqrt{{26}}}}{6}$
$latex =\frac{{2\pm i\sqrt{{26}}}}{3}$
Portanto, temos duas soluções para a equação quadrática:
$latex =\frac{{2+ i\sqrt{{26}}}}{3}$, $latex =\frac{{2- i\sqrt{{26}}}}{3}$
Calculadora de Raízes Complexas
Exercícios de raízes complexas de um polinômio para resolver
Aplique o que você aprendeu sobre raízes complexas para encontrar as raízes complexas dos polinômios quadráticos a seguir. Se precisar de ajuda com esses exercícios, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre raízes complexas? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
