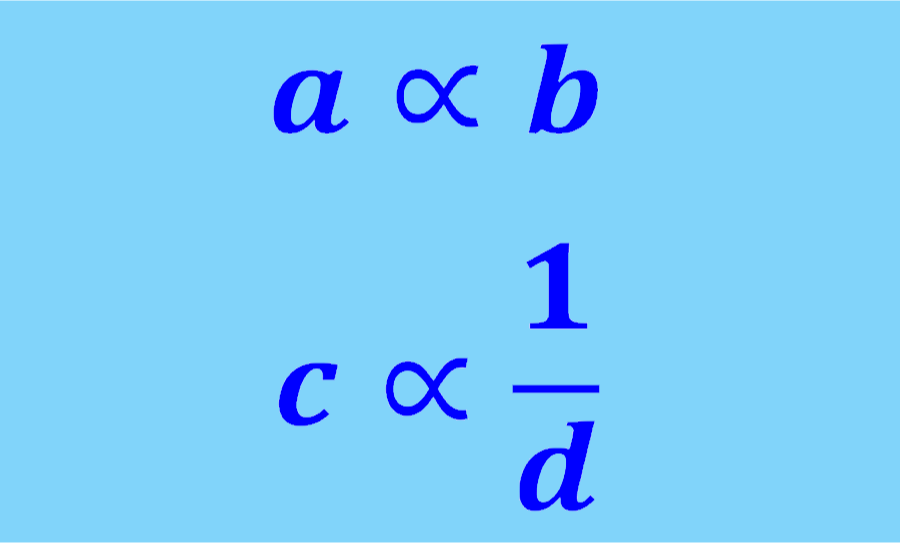A proporcionalidade direta e inversa nos permite comparar duas quantidades e entender como elas estão relacionadas. Quando duas quantidades são diretamente proporcionais, à medida que uma quantidade aumenta, a outra também aumenta. Quando duas quantidades são inversamente proporcionais, à medida que uma quantidade aumenta, a outra diminui.
Neste artigo, aprenderemos sobre a proporcionalidade direta e a proporcionalidade inversa. Além disso, aprenderemos sobre a regra de 3, que nos permite resolver facilmente problemas de proporcionalidade.
Definições de proporcionalidade direta e inversa
A proporcionalidade direta e inversa é usada para mostrar como duas quantidades estão relacionadas entre si. O símbolo usado para denotar proporcionalidade é “∝”. Por exemplo, se dissermos que a é proporcional a b, isso é representado por “a∝b“. Se dissermos que a é inversamente proporcional a b, isso é denotado como “a∝1/b“. Esses relacionamentos são regidos pelas mesmas regras de probabilidade.
Em ambos os casos, o valor de a muda quando b muda ou o valor de b muda quando a muda. A mudança em ambos os valores é equiparada a uma constante de proporcionalidade. Veremos exemplos mais tarde para entender isso completamente.
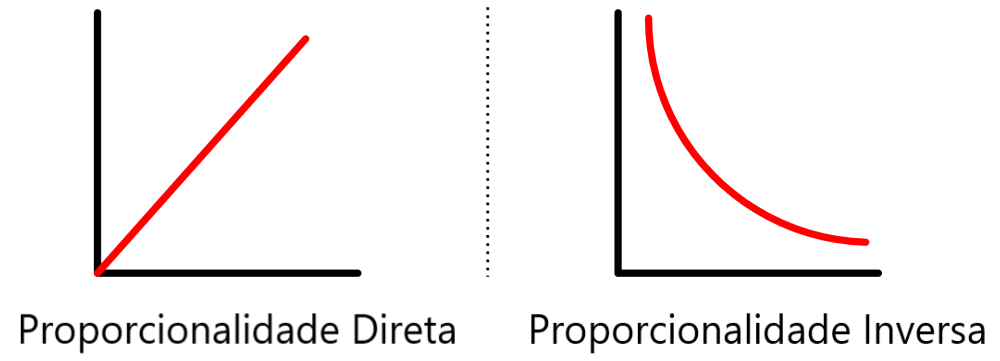
Proporcionalidade direta
Duas quantidades a e b têm uma proporcionalidade direta se aumentam ou diminuem juntas, ou seja, a razão de seus valores correspondentes permanece constante. Isso significa que temos:
$latex \frac{a}{b}=k$
onde k é um número positivo, então as variáveis a e b variam diretamente.
O símbolo usado para representar a proporção direta é “∝”.
Suponha que a seja proporcional a b. Isso pode ser escrito como:
a∝b
EXEMPLO
Suponha que temos $latex a=3b$. Isso mostra que a é proporcional a b e o valor de uma variável pode ser encontrado se soubermos o valor da outra variável.
Se tivermos que o valor de b é 5, $latex b=5$, então temos:
$latex a=3(5)=15$
Da mesma forma, se tivermos que o valor de a é 15, podemos encontrar o valor de b:
$latex 15=3b$
$latex b=5$
Regra de 3 direta
A regra de 3 é uma operação que nos ajuda a resolver problemas de proporcionalidade direta e inversa rapidamente.
Para usar a regra de 3, precisamos de três valores: dois proporcionais entre si e um terceiro. Com esses valores, podemos encontrar um quarto.
Vejamos o caso das proporções diretas. Vamos colocar os três valores a, b, c e o valor desconhecido x como segue e então aplicaremos a fórmula:
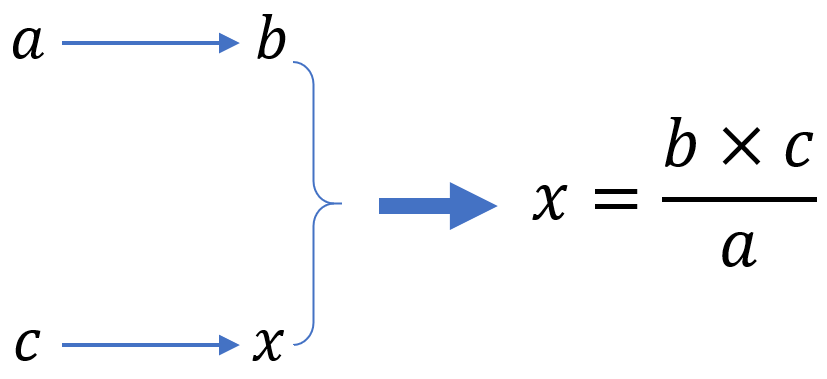
EXEMPLO
Felipe é pedreiro e constrói casas. Ele diz que leva 11 meses para construir 2 casas. Hoje ele recebeu uma oferta para construir 5 casas. Quantos meses ele levaria para construir as 5 casas?
Solução: Vamos formar uma tabela com os valores que conhecemos e encontraremos o valor desconhecido usando a fórmula:
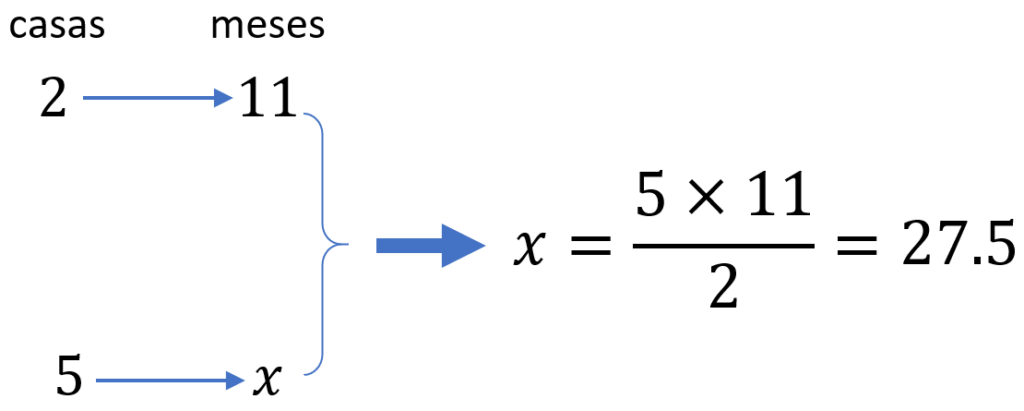
Então, ele levará 27,5 meses para construir 5 casas.
Experimente você mesmo – Resolva os exercícios
Proporcionalidade inversa
Dois valores são inversamente proporcionais quando um valor aumenta enquanto o outro diminui. Por exemplo, a e b são inversamente proporcionais se quando a aumenta, b diminui e vice-versa. Isso significa que o produto de seus valores correspondentes deve permanecer constante. Ou seja, se $latex ab = k$, então a e b são inversamente proporcionais.
O símbolo de probabilidade é usado de uma maneira diferente. O seguinte nos diz que a é inversamente proporcional a b:
a∝$latex \frac{1}{b}$
EXEMPLO
Suponha que temos $latex a=\frac{2}{b}$. Isso mostra que a é inversamente proporcional a b e o valor de uma variável pode ser encontrado se soubermos o valor da outra variável.
Se tivermos que o valor de b é 4, $latex b=4$, então temos:
$latex a=\frac{2}{4}=\frac{1}{2}$
Da mesma forma, se tivermos que o valor de a é 6, podemos encontrar o valor de b:
$latex 6=\frac{1}{b}$
$latex b =\frac{1}{6}$
Regra de 3 inversa
Agora vamos ver como aplicar a regra de 3 no caso de proporcionalidade inversa. Colocaremos os 3 valores conhecidos na tabela semelhante ao caso anterior, mas usaremos uma fórmula diferente:
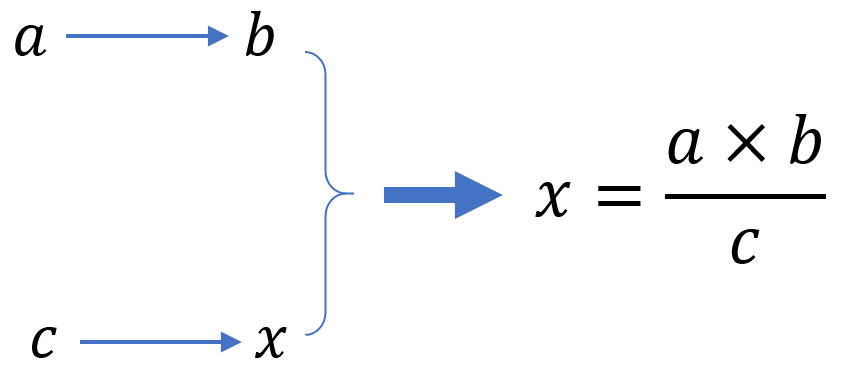
EXEMPLO
Em um armazém
eles estão transportando grandes quantidades de arroz. Usando 4 caminhões, cada um levaria 10 viagens para transportar toda a mercadoria. Se eles usarem 5 caminhões, quantas viagens cada um faria para transportar essa mercadoria?
Solução: Vamos formar uma tabela com os valores que conhecemos e usar a fórmula para obter o valor desconhecido:
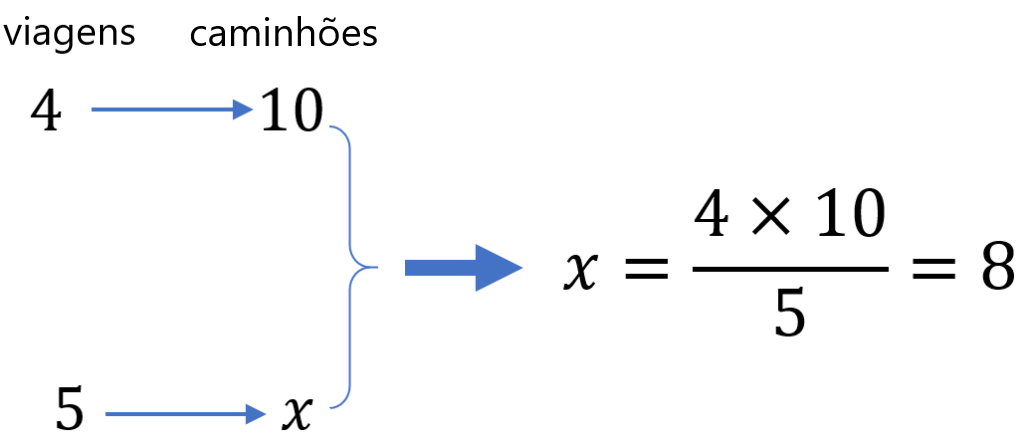
Então, usando 5 caminhões, seriam necessárias 8 viagens cada para transportar toda a mercadoria.
Experimente você mesmo – Resolva os exercícios
Veja também
Você quer aprender mais sobre vários tópicos algébricos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
