As funções da parte inteira são duas funções importantes usadas com frequência em matemática e computação. Existem duas funções de parte inteira, uma é a função piso e a outra é a função teto.
A seguir, veremos as definições, propriedades e gráficos dessas funções junto com vários exemplos com respostas.
Definição das funções piso e teto
Definição de função teto
Uma função teto é uma função na qual o menor inteiro sucessivo é retornado. Em outras palavras, a função tato de um número real x é o menor inteiro maior ou igual ao número x.
A notação usada para representar a função teto é $latex \lceil ~ \rceil$. Portanto, a função teto é $latex f(x)=\lceil x \rceil$.
Função de definição piso
A função piso, também conhecida como função piso, é definida como uma função que retorna o maior inteiro menor ou igual a x. A notação usada para representar a função piso é $latex \lfloor ~ \rfloor$. Portanto, a função piso é $latex f(x)=\lfloor x \rfloor$.
EXEMPLOS
- $latex \lceil 2.5 \rceil=3$
- $latex \lfloor 2.5 \rfloor=2$
- $latex \lceil 4.85 \rceil=5$
- $latex \lfloor 4.85 \rfloor=4$
Propriedades das funções piso e teto
As funções de piso e teto têm muitas propriedades úteis e interessantes. A seguir estão alguns dos mais importantes. Aqui, n é um inteiro:
- $latex \lfloor x \rfloor=n$ somente se $latex n\leq x<n+1$
- $latex \lceil x \rceil=n$ somente se $latex n-1<x\leq n$
- $latex \lfloor x \rfloor=n$ somente se $latex x-1< n\leq x$
- $latex \lceil x \rceil=n$ somente se $latex x\leq n<x+1$
- $latex \lceil -x \rceil=-\lceil x \rceil$
- $latex \lfloor -x \rfloor=-\lfloor x \rfloor$
- $latex \lceil x+n \rceil=\lceil x \rceil +n$
- $latex \lfloor x+n \rfloor=\lfloor x \rfloor +n$
Fórmulas das funções piso e teto
Fórmula da função teto
A fórmula para encontrar o valor teto para qualquer valor especificado é:
$latex f(x)=$ mínimo {$latex a\in Z; a\geq x$}
Isso significa que a função retorna o número inteiro mínimo que é maior ou igual a x. Isso é representado por:
$latex f(x)=<\lceil x \rceil=$ menor número inteiro sucessivo de x
Fórmula da função piso
A fórmula para encontrar o valor piso para qualquer valor especificado é:
$latex f(x)=$ mínimo {$latex a\in Z; a\geq x$}
Isso significa que a função retorna o número inteiro máximo que é menor ou igual a x . Isso é representado por:
$latex f(x)=\lfloor x \rfloor=$ maior número inteiro sucessivo de x
Gráficos das funções piso e teto
Os gráficos da função piso e teto têm uma forma em camadas e uma descontinuidade em cada ponto de número inteiro.
A seguir está o gráfico da função piso:
A seguir está o gráfico da função teto:
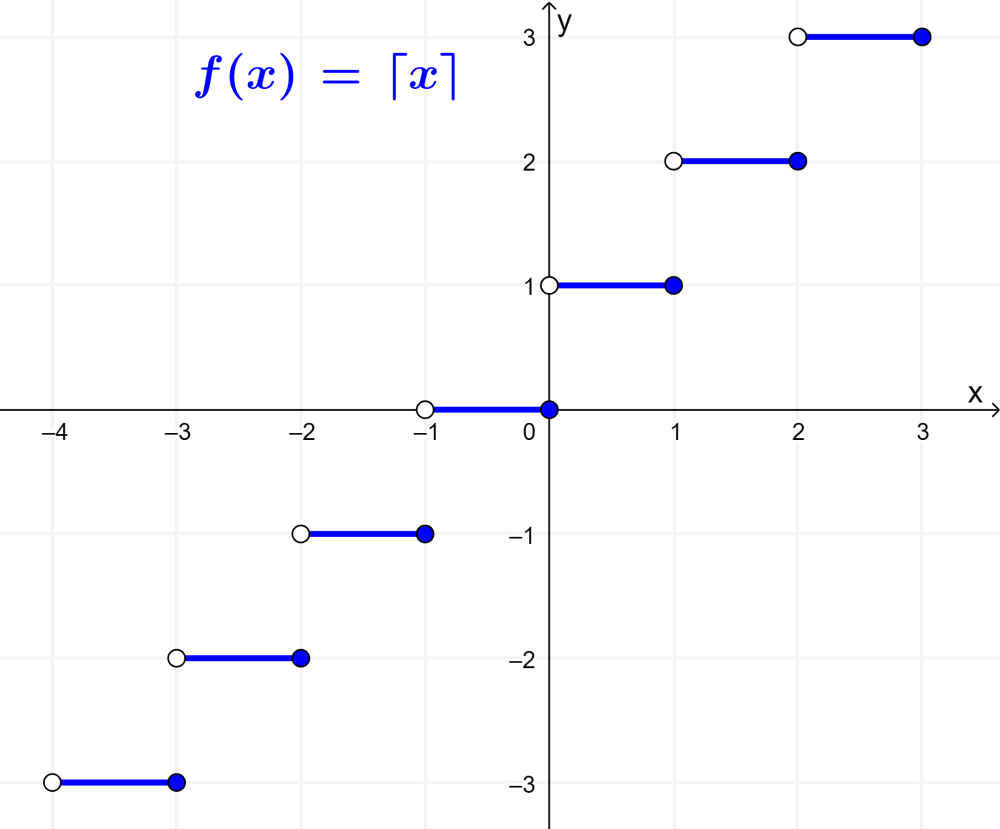
Funções piso e teto – Exercícios com resposta
EXERCÍCIO 1
Avalia a função teto de 3.4 e de -3.4.
Solução: Temos $latex f(3.4)=\lceil 3.4 \rceil=4$ e $latex f(-3.4)=\lceil -3.4 \rceil=-3$.
A função de teto de um número real é o menor inteiro maior ou igual a x. No caso de 3.4, os maiores inteiros são 4, 5, 6 … O menor deles é 4.
No caso de -3,4, os maiores inteiros são -3, -2, -1, … O menor deles é -3.
EXERCÍCIO 2
Qual é o resultado de $latex \lfloor \sqrt{46} \rfloor$?.
Solução: Neste caso, temos que encontrar o maior inteiro que seja igual ou menor que $latex \sqrt{46}$.
Sabemos que $latex \sqrt{36}<\sqrt{46}<\sqrt{49}$.
Então, temos $latex 6<\sqrt{46}<7$.
Portanto, $latex \lfloor \sqrt{46} \rfloor=6$.
EXERCÍCIO 3
Resolva a equação $latex \lfloor x-\frac{1}{2} \rfloor +\lfloor x-\frac{5}{2} \rfloor +\lfloor x-\frac{9}{2} \rfloor =3$.
Solução: Podemos resolver este problema mais facilmente usando a substituição $latex x-\frac{1}{2}=z$. Então, temos a equação:
$latex \lfloor z \rfloor +\lfloor z-2 \rfloor +\lfloor z-4 \rfloor =3$
Usando a identidade $latex \lfloor x+n \rfloor =\lfloor x \rfloor +n$, temos o seguinte:
$latex \lfloor z \rfloor +\lfloor z \rfloor -2+\lfloor z \rfloor -4=3$
⇒ $latex 3\lfloor z \rfloor =9$
⇒ $latex \lfloor z \rfloor =3$
A última equação significa que $latex 3\leq z<4$. Voltando à variável x, temos:
$latex 3\leq x-\frac{1}{2}<4$
⇒ $latex 3\frac{1}{2}\leq x<4\frac{1}{2}$
⇒ $latex x\in[3.5, 4.5)$
Funções piso e teto – Exercícios para resolver
Veja também
Você quer aprender mais sobre funções? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
