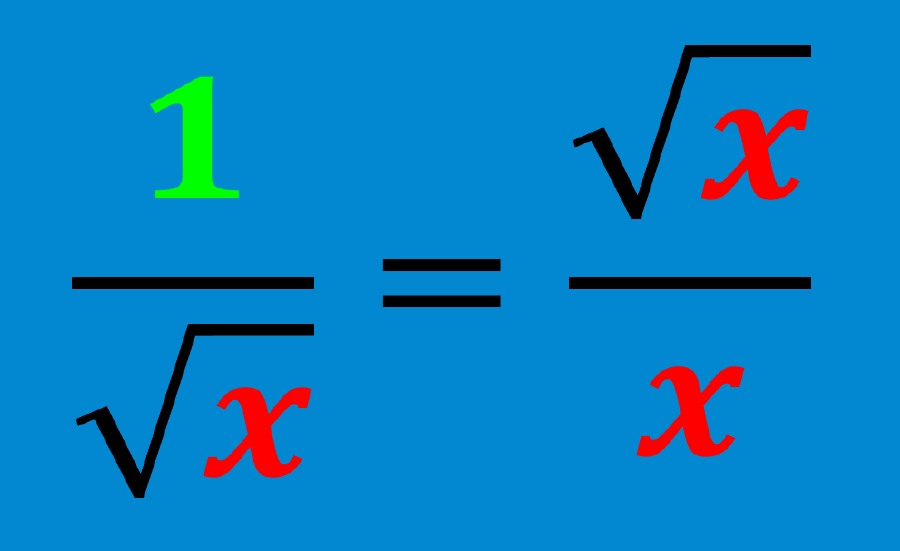Racionalização é o processo de remoção de radicais do denominador de uma fração. Para racionalizar os denominadores, devemos multiplicar a expressão por um valor conveniente para que, ao simplificar, eliminemos os radicais do denominador. Existem dois métodos principais usados para racionalizar os radicais, dependendo se o denominador é monomial ou binomial.
A seguir, veremos um resumo desses dois métodos, juntamente com vários exercícios de racionalização para dominar totalmente esse processo.
Resumo de racionalização de denominadores
Racionalizar o denominador significa eliminar as expressões radicais no denominador para que não tenhamos raízes quadradas, cúbicas ou outros. A ideia principal na racionalização dos denominadores é multiplicar a fração original por um valor apropriado para que, após a simplificação, o denominador não contenha mais radicais.
Quando o denominador é um monomial, podemos aplicar o fato de que:
$latex \sqrt{x} \cdot \sqrt{x}=\sqrt{{{x}^2}}=x$
Portanto, podemos multiplicar o numerador e o denominador pela expressão radical. Depois de simplificar, obteremos uma expressão sem radicais no denominador.
Por outro lado, se o denominador for um binomial, devemos usar o conjugado do binomial. O conjugado de um binômio é igual ao mesmo binômio, mas com o sinal do meio alterado.
Por exemplo, suponha que temos o binômio $latex a+\sqrt{b}$ no denominador. O conjugado desse binômio é $latex a- \sqrt{b}$. O produto do binômio e seu conjugado é:
$latex (a+\sqrt{b})(a- \sqrt{b})={{a}^2}-b$
Exercícios de racionalização de denominadores resolvidos
O processo de racionalização indicado acima é usado para racionalizar monômios e binômios nos exercícios a seguir. Tente resolver os exercícios sozinho antes de olhar para a solução.
EXERCÍCIO 1
Racionalize o denominador da expressão $latex \frac{3}{\sqrt{2}}$.
Solução
O denominador contém uma expressão radical, a raiz quadrada de 2. Podemos remover o radical do denominador multiplicando-o por ele mesmo, pois $latex \sqrt{2}\times \sqrt{2}=2$.
No entanto, se apenas multiplicarmos para o denominador, estamos mudando para a expressão. Portanto, também multiplicamos o numerador para equilibrar.
Multiplicando a expressão por $latex \frac{\sqrt{2}}{\sqrt{2}}$ na verdade, estamos multiplicando por 1. Portanto, temos:
$latex \frac{3}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}=\frac{3\sqrt{2}}{\sqrt{4}}$
$latex =\frac{3\sqrt{2}}{2}$
A expressão que obtivemos não tem mais radicais no denominador, portanto já a racionalizamos.
EXERCÍCIO 2
Racionalize $latex \frac{8}{\sqrt{2}}$ e simplifique se possível.
Solução
Semelhante ao exercício anterior, temos uma raiz quadrada de 2 no denominador. Então, multiplicamos a expressão por $latex \frac{\sqrt{2}}{\sqrt{2}}$:
$latex \frac{8}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}=\frac{8\sqrt{2}}{\sqrt{4}}$
$latex =\frac{8\sqrt{2}}{2}$
Já racionalizamos para a expressão, mas, neste caso, também podemos simplificar cancelando fatores comuns:
$latex \frac{8\sqrt{2}}{2}=4\sqrt{2}$
EXERCÍCIO 3
Racionalize a expressão $latex \sqrt{\frac{5}{3}}$.
Solução
Nesse caso, temos a raiz quadrada de uma fração completa. Podemos começar aplicando a regra do quociente de raízes quadradas. Isso nos permite escrever o numerador e o denominador com raízes quadradas separadamente. Então, temos:
$latex \sqrt{\frac{5}{3}}=\frac{\sqrt{5}}{\sqrt{3}}$
A nova expressão tem um denominador com raiz quadrada de 3, então multiplicamos o numerador e o denominador por este radical:
$latex \frac{\sqrt{5}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{5}\sqrt{3}}{\sqrt{9}}$
$latex =\frac{\sqrt{5}\sqrt{3}}{3}$
$latex =\frac{\sqrt{15}}{3}$
EXERCÍCIO 4
Simplifique racionalizando o denominador de $latex \frac{3 \sqrt{6}}{\sqrt{3}}$.
Solução
Multiplicamos o numerador e o denominador por $latex \sqrt{3}$ para eliminar o radical do denominador:
$latex \frac{3\sqrt{6}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}=\frac{3\sqrt{18}}{\sqrt{9}}$
$latex =\frac{3\sqrt{18}}{3}$
$latex =\sqrt{18}$
Podemos reescrever 18 como o produto de 9 e 2 para simplificar para a expressão:
$latex \sqrt{18}=\sqrt{9\times 2}$
$latex =\sqrt{9}\sqrt{2}$
$latex =3\sqrt{2}$
EXERCÍCIO 5
Racionalize e simplifique a expressão $latex \frac{4-\sqrt{6}}{\sqrt{2}}$.
Solução
Esta expressão contém um binômio no numerador, mas o processo é o mesmo, pois ainda temos um monômio no denominador. Multiplicamos o numerador e o denominador por $latex \sqrt{2}$:
$latex \frac{4-\sqrt{6}}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}(4-\sqrt{6})}{\sqrt{4}}$
$latex =\frac{4\sqrt{2}-\sqrt{12}}{2}$
Podemos simplificar a expressão reconhecendo que podemos escrever 12 como o produto de 4 e 3:
$latex \frac{4\sqrt{2}-\sqrt{12}}{2}=\frac{4\sqrt{2}-\sqrt{4\times 3}}{2}$
$latex =\frac{4\sqrt{2}-\sqrt{4}\sqrt{3}}{2}$
$latex =\frac{4\sqrt{2}-2\sqrt{3}}{2}$
$latex =2\sqrt{2}-\sqrt{3}$
EXERCÍCIO 6
Racionalize a expressão $latex \frac{4}{2+\sqrt{2}}$.
Solução
Este exercício é um pouco diferente, pois temos dois termos no denominador, ou seja, um binômio. Para eliminar o radical do denominador, temos que multiplicar o numerador e o denominador pelo conjugado do binômio.
Para encontrar o conjugado de um binômio, simplesmente temos que mudar o sinal do meio. Neste caso, temos que multiplicar por $latex \frac{2-\sqrt{2}}{2-\sqrt{2}}$:
$latex \frac{4}{2+\sqrt{2}}\times \frac{2-\sqrt{2}}{2-\sqrt{2}}=\frac{4(2-\sqrt{2})}{(2+\sqrt{2})(2-\sqrt{2})}$
$latex =\frac{8-4\sqrt{2}}{4-2\sqrt{2}+2\sqrt{2}-\sqrt{4}}$
$latex =\frac{8-4\sqrt{2}}{4-2}$
$latex =\frac{8-4\sqrt{2}}{2}$
$latex =4-2\sqrt{2}$
EXERCÍCIO 7
Racionalize a expressão $latex \frac{5}{6- \sqrt{3}}$.
Solução
Semelhante ao problema anterior, temos que multiplicar o numerador e o denominador pelo conjunto do binômio. Neste caso, temos que multiplicar por $latex \frac{6+\sqrt{3}}{6+\sqrt{3}}$:
$latex \frac{5}{6-\sqrt{3}}\times \frac{6+\sqrt{3}}{6+\sqrt{3}}=\frac{5(6+\sqrt{3})}{(6-\sqrt{3})(6+\sqrt{3})}$
$latex =\frac{30+5\sqrt{3}}{36-6\sqrt{3}+6\sqrt{3}-\sqrt{9}}$
$latex =\frac{30+5\sqrt{3}}{36-3}$
$latex =\frac{30+5\sqrt{3}}{33}$
EXERCÍCIO 8
Racionalize a expressão $latex \frac{\sqrt{3}- \sqrt{2}}{\sqrt{3}+\sqrt{2}}$.
Solução
Multiplicamos o denominador e o numerador pelo conjugado do binômio. Neste caso, o conjugado é $latex \sqrt{3}-\sqrt{2}$:
$latex \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}=\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}\times \frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}-\sqrt{2}}$
$latex =\frac{(\sqrt{3}-\sqrt{2})(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$
$latex =\frac{\sqrt{9}-\sqrt{6}-\sqrt{6}+\sqrt{4}}{\sqrt{9}-\sqrt{6}+\sqrt{6}-\sqrt{4}}$
$latex =\frac{3-2\sqrt{6}+2}{3-2}$
$latex =3-2\sqrt{6}+2$
$latex =5-2\sqrt{6}$
Exercícios de racionalização de denominadores para resolver
Use o que você aprendeu sobre racionalização para resolver os exercícios a seguir. Escolha uma resposta e verifique para ter certeza de que selecionou a correta.
Veja também
Você quer aprender mais sobre tópicos algébricos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
