A transformação de uma função nos permite fazer modificações em seu gráfico. Uma dessas transformações é o alongamento e compressão de funções. Podemos comprimir ou alongar a função em torno do eixo x quando temos f(ax) e podemos comprimir ou alongar a função em torno do eixo y quando temos af(x) onde a é uma constante.
A seguir, aprenderemos como alongar ou comprimir uma função em relação ao eixo x e ao eixo y.
Alongamentos e compressões de uma função em relação ao eixo x e ao eixo y
Alongamentos e compressões são transformações que são produzidas quando os valores x ou y da função original são multiplicados por um valor constante.
Para entender os alongamentos e compressões em relação ao eixo x e ao eixo y, vamos usar a função $latex f(x)=x+1$. Fazendo o gráfico desta função, obtemos a seguinte reta:
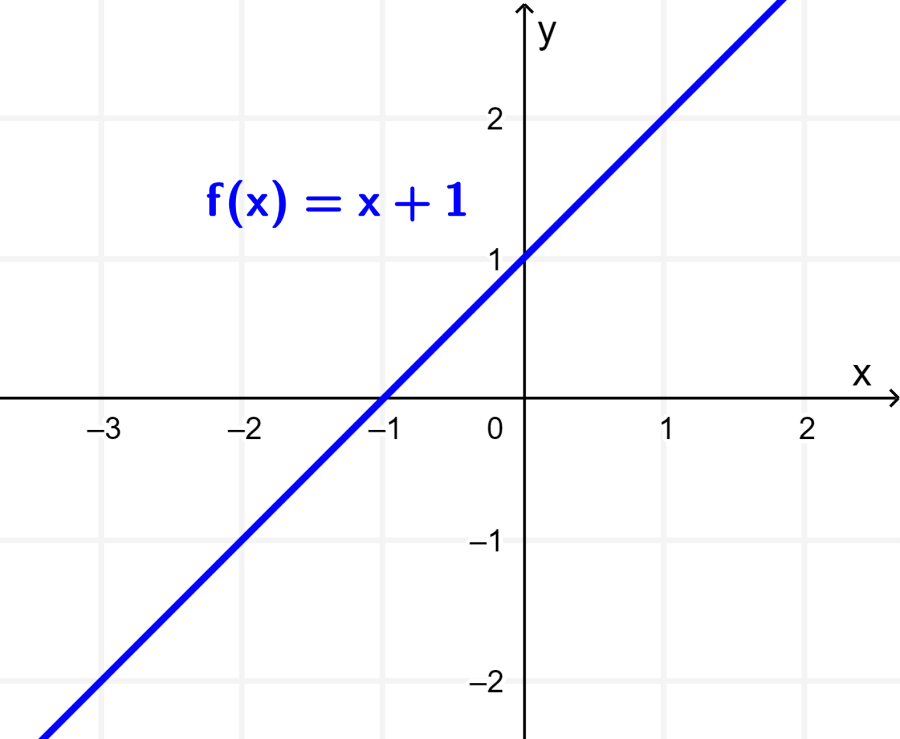
Para produzir alongamentos e compressões, vamos multiplicar os valores x ou y da função $latex f(x)$ por uma constante. Assim, temos (i) $latex f(2x)$ e (ii) $latex 2f(x)$. Simplificando, temos:
(i) $latex f(2x)=(2x)+1~$ e (ii) $latex 2f(x)=2(x+1)$
(i) $latex f(2x)=2x+1~$ e (ii) $latex 2f(x)=2x+2$
Quando plotamos as funções (i) e (ii) junto com a função original $latex f(x)$, temos:
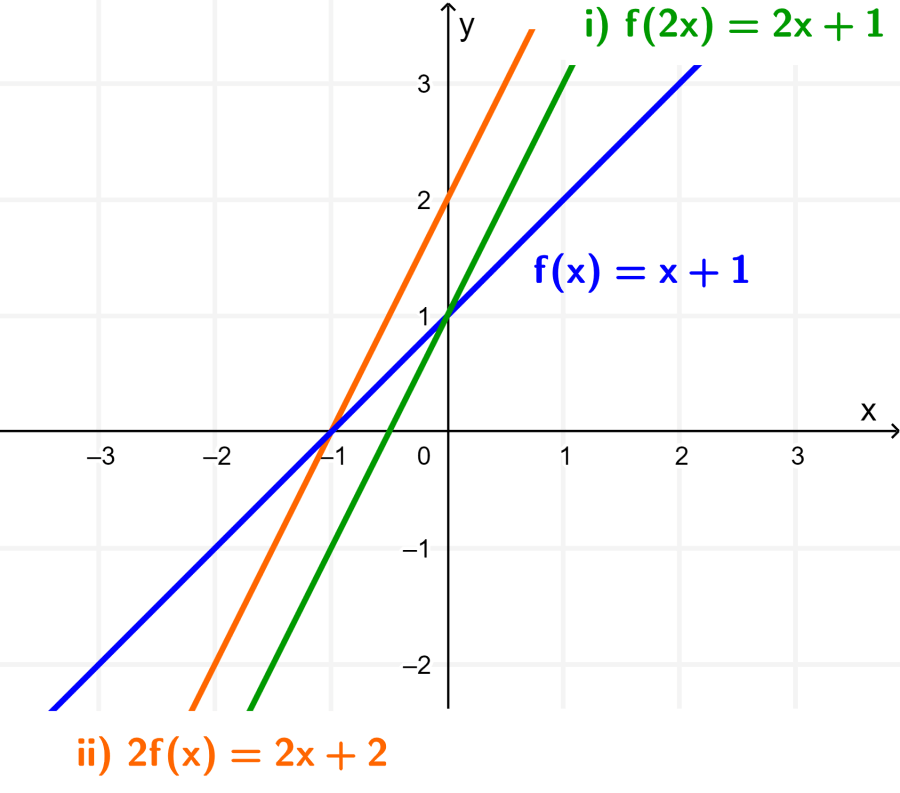
Na transformação (i), o gráfico de $latex f(x)$ foi esticado em torno do eixo x por um fator de $latex \frac{1}{2}$ (a função foi reduzida pela metade)
Na transformação (ii), o gráfico de $latex f(x)$ foi esticado em torno do eixo y por um fator de 2.
Resumindo, temos:
- A transformação $latex f(ax)$ resulta em um alongamento em torno do eixo x por um fator de $latex \frac{1}{a}$.
- A transformação $latex af(x)$ resulta em um alongamento em torno do eixo y por um fator de $latex a$.
- Se o fator de estiramento estiver entre 0 e 1, a transformação é uma compressão do gráfico.
Exemplos de alongamento e compressão de funções
Os exemplos a seguir usam as transformações de alongamento e compressão de funções. Cada exemplo tem uma solução detalhada, mas tente resolver os exercícios primeiro.
EXEMPLO 1
Obtenha o gráfico da função $latex f(x)=x+2$, e então faça o gráfico da função $latex g(x)=3f(x)$.
Solução
O gráfico da função $latex f(x)=x+2$ é uma reta que intercepta o eixo y em (0, 2) e o eixo x em (-2, 0):
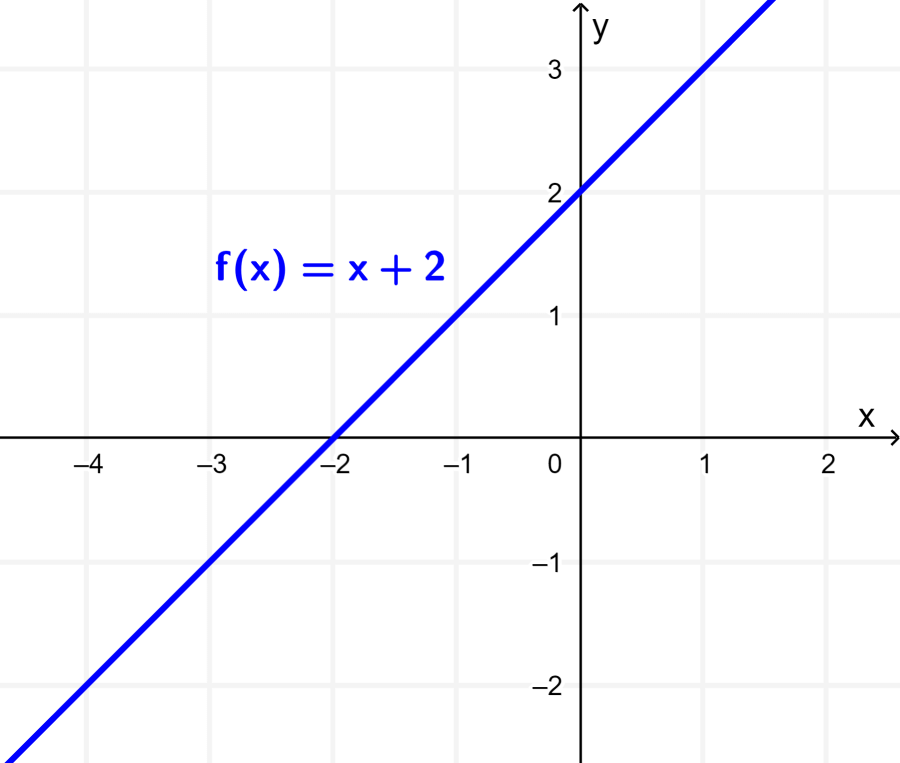
A função g é dada por $latex g(x)=3f(x)=3x+6$. O gráfico desta função é igual ao gráfico de f esticado por um fator de 3 em torno do eixo y.
.
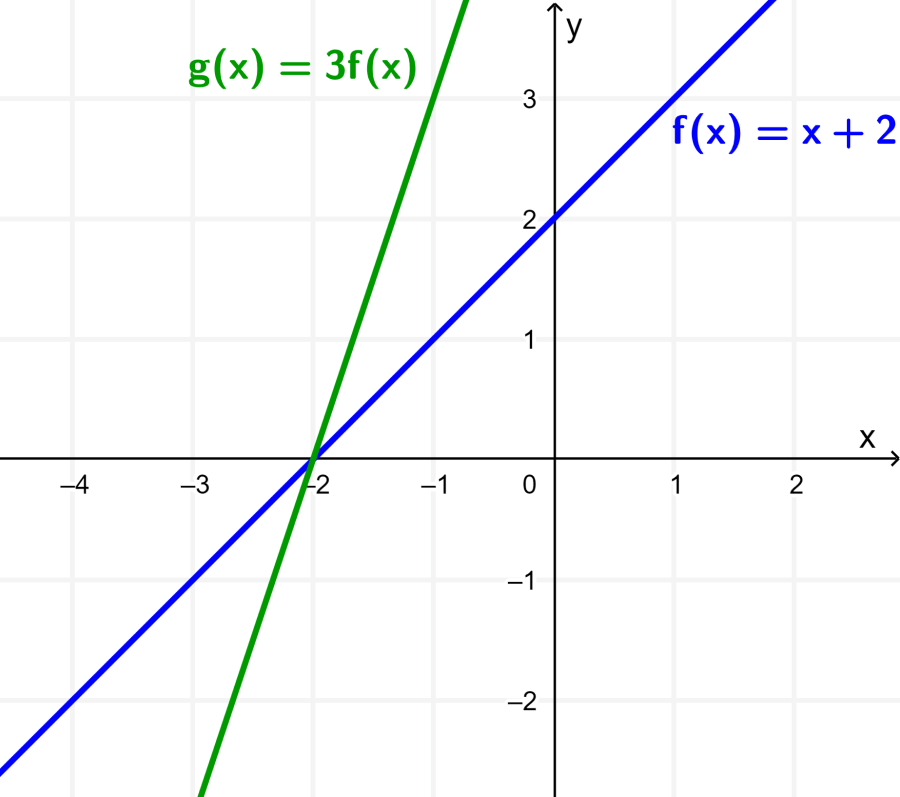
EXEMPLO 2
Qual é a diferença entre os gráficos de $latex f(x)=\cos(x)$ e os gráficos de $latex g(x)=\cos(2x)$ e $latex h(x)=\cos( \frac{1}{2}x)$?
Solução
Quando aplicamos a transformação $latex g(x)=f(ax)$, onde a é uma constante, produzimos um alongamento ou compressão em torno do eixo x.
Então, podemos olhar para o gráfico da função cosseno padrão $latex f(x)=\cos(x)$ junto com as outras duas funções:
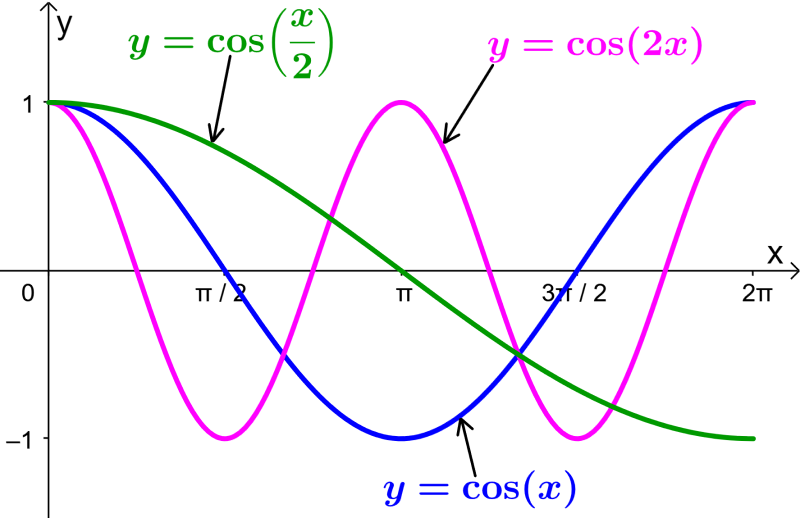
Vemos que o gráfico de $latex g(x)=\cos(2x)$ é dividido pela metade, ou seja, o fator de estiramento é $latex \frac{1}{a}=\frac{1}{2 }$.
No caso do gráfico de $latex h(x)=\cos(\frac{1}{2}x)$, a função é alongada. O fator de estiramento é $latex \frac{1}{a}=\frac{1}{\frac{1}{2}}=2$.
EXEMPLO 3
Faça o gráfico das funções $latex g(x)=2|x|$ e $latex h(x)=0,5|x|$.
Solução
Neste caso, temos a função de valor absoluto, que em sua forma base, $latex f(x)=|x|$, tem o seguinte gráfico:
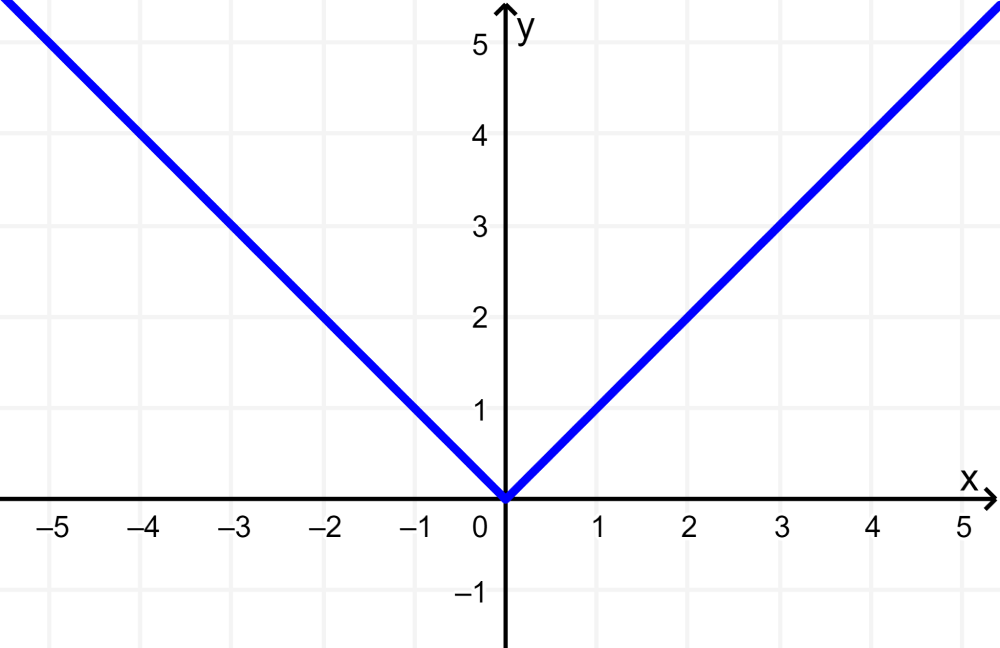
Agora, as funções g e h são obtidas aplicando trechos em relação ao eixo y. Ou seja, temos $latex g(x)=2f(x)$ e $latex h(x)=0,5f(x)$.
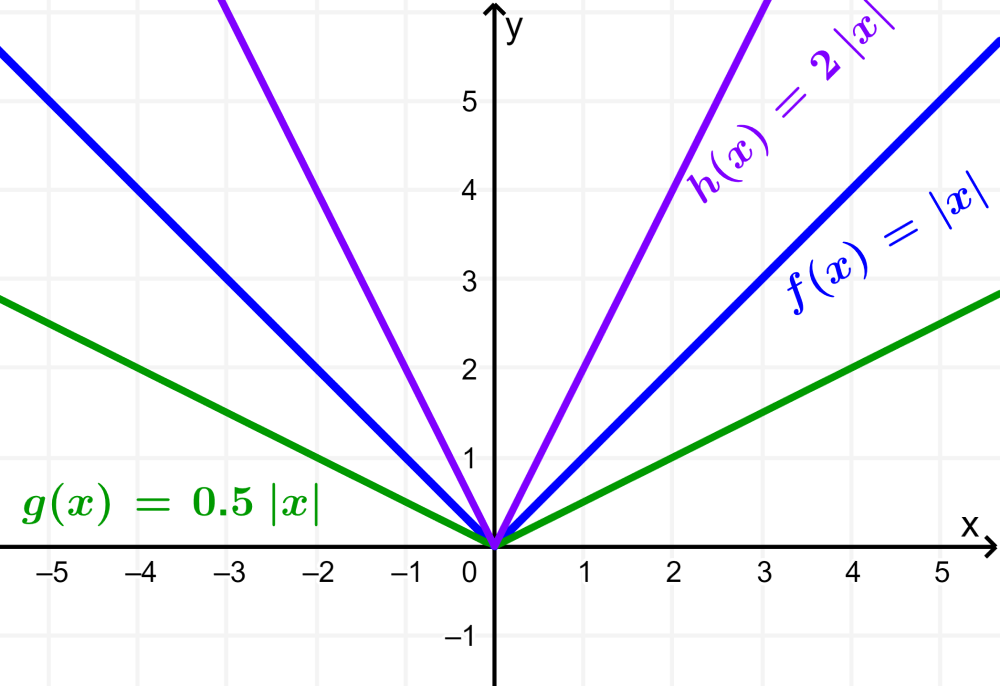
Vemos que a função h é esticada por um fator de 2 e a função g por um fator de 0,5 (igual a uma compressão pela metade).
EXEMPLO 4
Que mudanças precisamos fazer na função $latex f(x)=3x^2+6x$ se quisermos esticá-la por um fator de 3 em torno do eixo x?
Solução
Para esticar uma função por um fator de 3 em torno do eixo x, temos que aplicar a transformação $latex g(x)=f(\frac{1}{3}x)$.
Isso significa que temos que substituir a variável x em f por $latex \frac{1}{3}x$. Então temos:
$latex g(x)=f(\frac{1}{3}x)$
$latex g(x)=3(\frac{1}{3}x)^2+6(\frac{1}{3}x)$
$latex g(x)=3(\frac{1}{9})x^2+2x$
$latex g(x)=\frac{1}{3}x^2+2x$
Exercícios de alongamento e compressão de funções para resolver
Aplique tudo o que aprendeu sobre as funções de alongamento e compressão para resolver os exercícios a seguir.
Veja também
Interessado em aprender mais sobre transformações de funções? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
