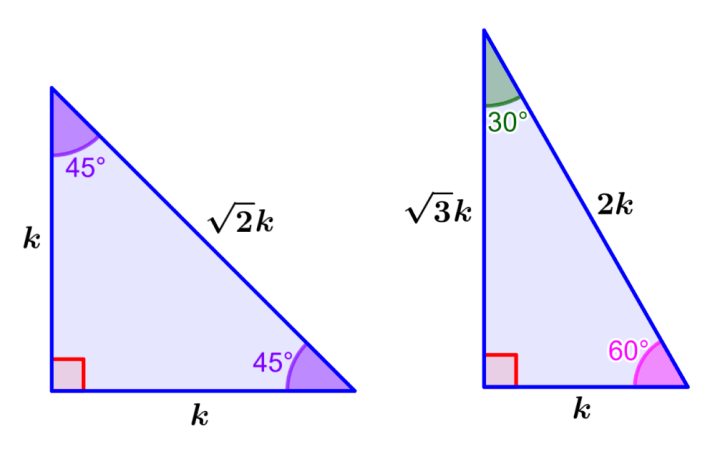
Triângulos especiais são triângulos retângulos com proporções especiais de seus lados. O triângulo 30°-60°-90° tem as proporções 1:√3:2. O triângulo 45°-45°-90° tem as proporções 1:1:√2. Todos os comprimentos desses lados podem ser facilmente encontrados se soubermos apenas o comprimento de um dos lados.
A seguir, aprenderemos mais sobre esses triângulos especiais. Aprenderemos a derivar suas proporções e resolveremos alguns exercícios práticos.
Triângulo especial 45°-45°-90°
Um triângulo de 45°-45°-90° é um triângulo retângulo que tem dois ângulos agudos com medida de 45°. Isso significa que esses triângulos também são isósceles e possuem lados com proporções especiais.
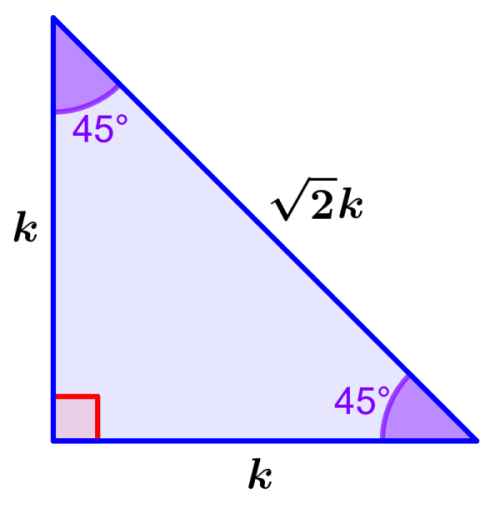
As proporções desses triângulos podem ser obtidas usando o teorema de Pitágoras. Como esses triângulos têm dois ângulos com as mesmas medidas, seus lados opostos devem ter o mesmo comprimento.
Então, usando o teorema de Pitágoras, podemos supor que os dois lados iguais têm comprimento 1 unidade, então a hipotenusa é:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{1}^2}+{{1}^2}$
$latex {{c}^2}=2$
$latex c=\sqrt{2}$
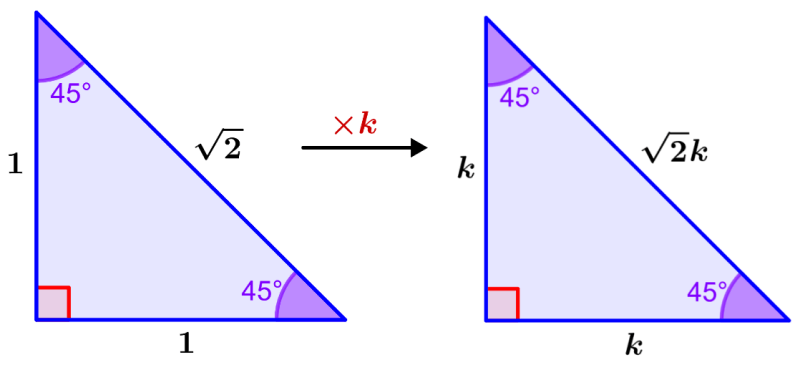
Podemos dimensionar o triângulo por um fator de k. Como estamos apenas dimensionando o triângulo sem alterar nenhum de seus ângulos, obtemos as razões dos comprimentos dos lados do triângulo 45°-45°-90°.
Triângulo especial 30°-60°-90°
Um triângulo de 30°-60°-90° é um triângulo retângulo contendo os ângulos agudos 30° e 60°. Os lados desses triângulos têm comprimentos com proporções especiais.
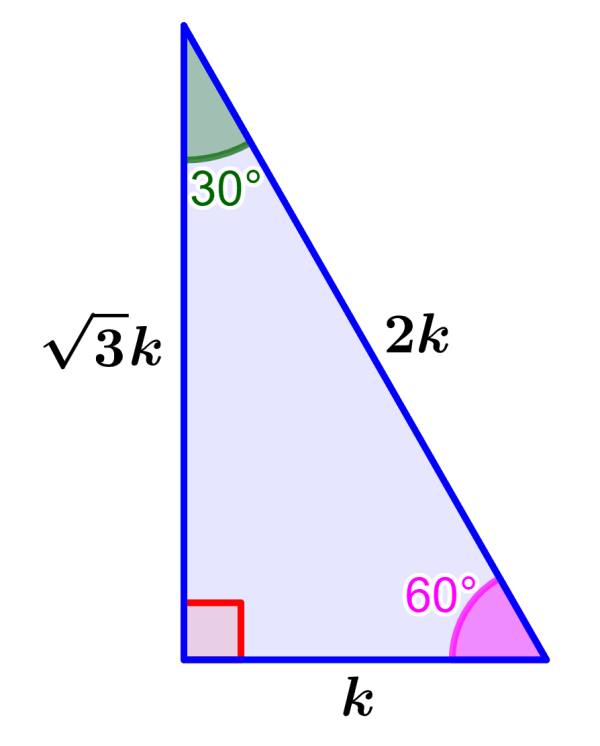
Podemos obter essas razões usando o teorema de Pitágoras. Para isso, podemos considerar o triângulo 30°-60°-90° como metade de um triângulo equilátero, conforme mostrado no diagrama abaixo.
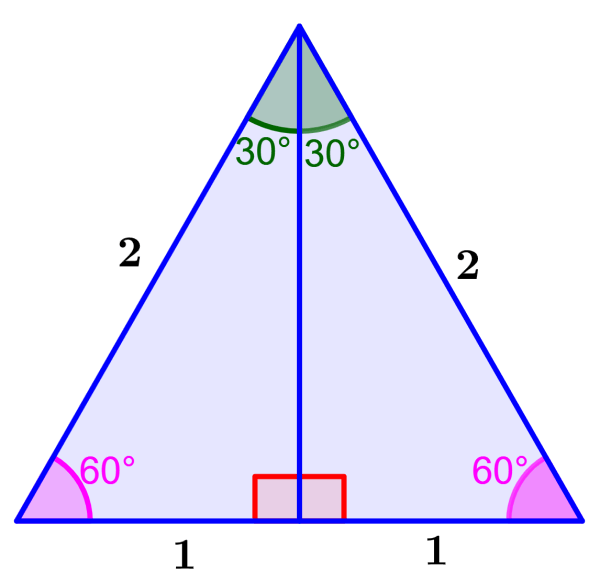
Podemos supor que um dos lados curtos do triângulo 30°-60°-90° tem um comprimento de 1 unidade. Assim, a base do triângulo equilátero medirá 2 unidades e a hipotenusa do triângulo 30°-60°-90° também medirá 2 unidades, pois um triângulo equilátero tem todos os seus lados iguais em comprimento.
Com isso, podemos calcular o comprimento da segunda perna do triângulo 30°-60°-90°:
$latex {{a}^2}+{{b}^2}={{c}^2}$
$latex {{1}^2}+{{b}^2}={{2}^2}$
$latex 1+{{b}^2}=4$
$latex {{b}^2}=3$
$latex b=\sqrt{3}$
Agora, podemos dimensionar o triângulo por um fator de k. Ao dimensionar, estamos apenas alterando os comprimentos dos lados, mas mantendo os ângulos e as proporções. Assim, obtemos as proporções gerais do triângulo 30°-60°-90°.
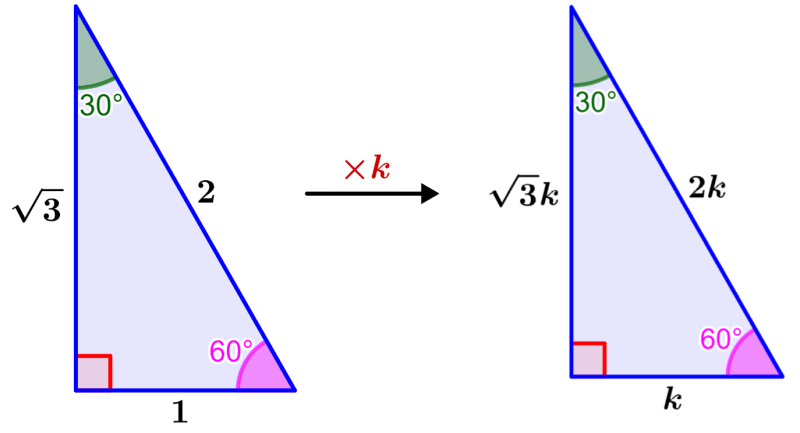
Exercícios resolvidos de triângulos especiais
EXERCÍCIO 1
Determine a medida do lado x no triângulo a seguir.
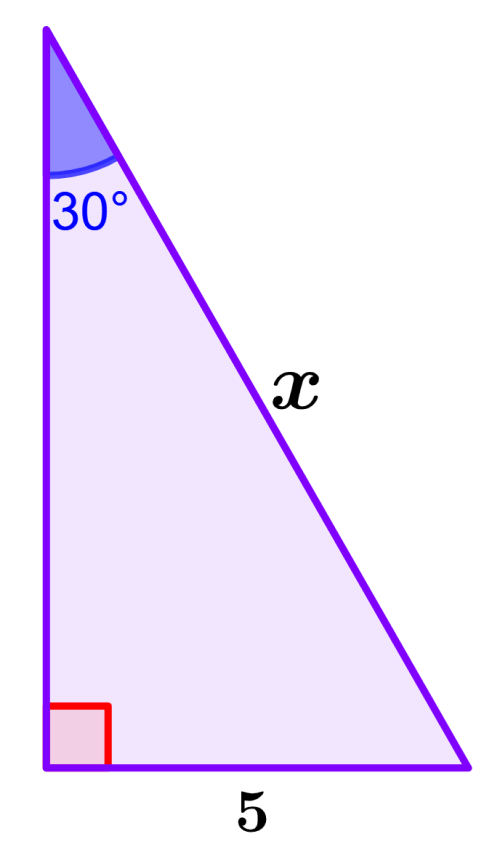
Solução: Este é um triângulo de 30°-60°-90° e sabemos que esses triângulos têm as razões 1:2:√3. O lado que mede 5 unidades corresponde ao ângulo de 30° e o lado que procuramos corresponde ao ângulo de 90°. Então, a razão deles é 2 e temos:
$latex x=5\times 2$
$latex x=10$
O lado x é 10 unidades.
EXERCÍCIO 2
Qual é a medida do lado x no triângulo a seguir?
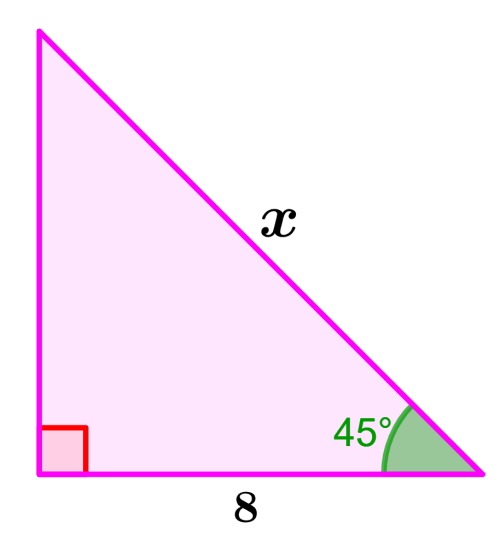
Solução: Este é um triângulo de 45°-45°-90° e sabemos que esses triângulos têm as razões 1:1:√2. O lado com a medida de 8 unidades corresponde a uma das pernas opostas ao ângulo de 45° e o lado que procuramos corresponde ao lado oposto ao ângulo de 90°.
Então a razão do lado x é √2. Portanto, temos:
$latex x=8\sqrt{2}$
EXERCÍCIO 3
Determine a medida de x no triângulo a seguir.
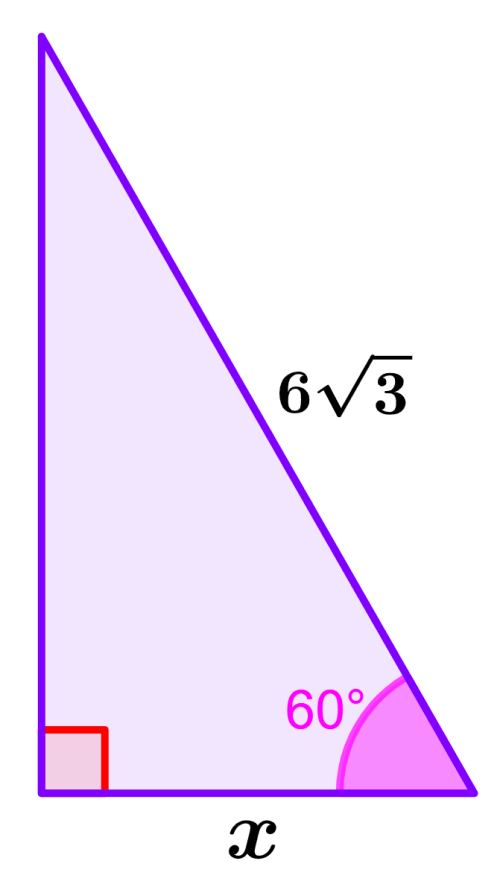
Solução: Este é um triângulo de 30°-60°-90°. Então sabemos que suas razões são 1:√3:2. Conhecemos o comprimento do lado oposto ao ângulo de 90°, ou seja, o lado que tem razão 2.
Queremos encontrar a medida do lado x que é oposto ao ângulo de 30°, ou seja, o lado que tem proporção 1. Então, dividimos por 2 para encontrar sua medida:
$latex x=\frac{6\sqrt{3}}{2}$
$latex x=3\sqrt{3}$
Veja também
Interessado em aprender mais sobre triângulos e a desigualdade triangular? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
