A soma dos ângulos internos de qualquer polígono sempre permanece constante, independentemente de o polígono ser regular ou irregular. Podemos calcular a soma aplicando uma fórmula que usa o número de lados do polígono. Por sua vez, a fórmula é derivada considerando que todos os polígonos podem ser divididos em triângulos.
A seguir, conheceremos a fórmula que podemos usar para encontrar a soma dos ângulos internos de polígonos. Em seguida, usaremos esta fórmula para resolver alguns exercícios práticos.
GEOMETRIA
Relevante para…
Aprender a determinar a soma dos ângulos internos de um polígono.
GEOMETRIA
Relevante para…
Aprender a determinar a soma dos ângulos internos de um polígono.
Fórmula para encontrar a soma dos ângulos internos de um polígono
A soma dos ângulos internos de qualquer polígono pode ser calculada usando a seguinte fórmula:
| $latex (n-2)\times 180$° |
Aqui, n representa o número de lados do polígono. Por exemplo, para um pentágono, usamos $latex n=5$ e para um hexágono, usamos $latex n=6$.
Podemos aplicar esta fórmula independentemente de o polígono ser regular ou irregular, pois um polígono com um determinado número de lados sempre tem a mesma soma dos ângulos internos.
Por exemplo, um pentágono tem 5 lados, então podemos encontrar a soma de seus ângulos aplicando a fórmula com $latex n=5$:
$latex (n-2)\times 180$°
$latex =(5-2)\times 180$°
$latex =(3)\times 180$°
$latex =540$°
Agora, para calcular a soma dos ângulos internos de um heptágono, usamos $latex n=7$:
$latex (n-2)\times 180$°
$latex =(7-2)\times 180$°
$latex =(5)\times 180$°
$latex =900$°
Na tabela a seguir, podemos ver a soma dos ângulos internos de alguns polígonos comuns:
| Polígono | Número de lados | Soma de ângulos |
| Triângulo | 3 | 180° |
| Quadrilátero | 4 | 360° |
| Pentágono | 5 | 540° |
| Hexágono | 6 | 720° |
| Heptágono | 7 | 900° |
| Octógono | 8 | 1080° |
| Nonágono | 9 | 1260° |
| Decágono | 10 | 1440° |
Determine a medida dos ângulos internos individuais de um polígono regular
Um polígono regular tem todos os seus lados com a mesma medida e todos os seus ângulos internos com a mesma medida. Isso significa que podemos determinar a medida de um dos ângulos internos dividindo a soma total dos ângulos pelo número de lados do polígono.
Além disso, podemos obter uma fórmula para a medida individual de um ângulo interno de um polígono regular a partir da fórmula da soma dos ângulos. Então temos:
| $latex \frac{(n-2)\times 180}{n}$ |
onde, n representa o número de lados do polígono regular.
Por exemplo, para determinar a medida de um ângulo interno de um quadrado, usamos $latex n=4$. Observando a tabela acima, vemos que a soma dos ângulos internos de um quadrado é igual a 360°. Então, dividindo por 4, temos:
360°÷4=90°
Um ângulo interno de um quadrado mede 90°.
Da mesma forma, podemos determinar a medida dos ângulos internos de um heptágono. Para isso, olhamos a tabela de soma de ângulos e dividimos a soma total por 7. Assim, vemos que a soma total é 900° e temos:
900°÷7=128.57°
Um ângulo interno de um heptágono mede 128,57°.
Como derivar a fórmula para a soma dos ângulos internos?
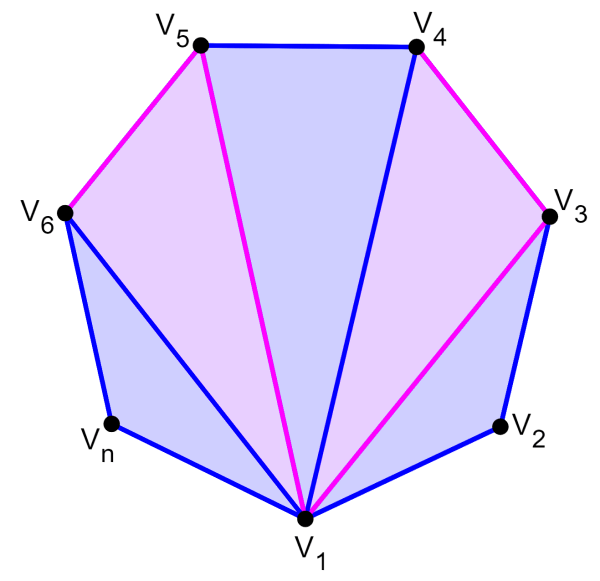
A fórmula da soma dos ângulos internos de um polígono é derivada considerando que podemos dividir um polígono em vários triângulos. Por exemplo, o seguinte polígono que tem os vértices $latex V_{1}$ a $latex V_{n}$.
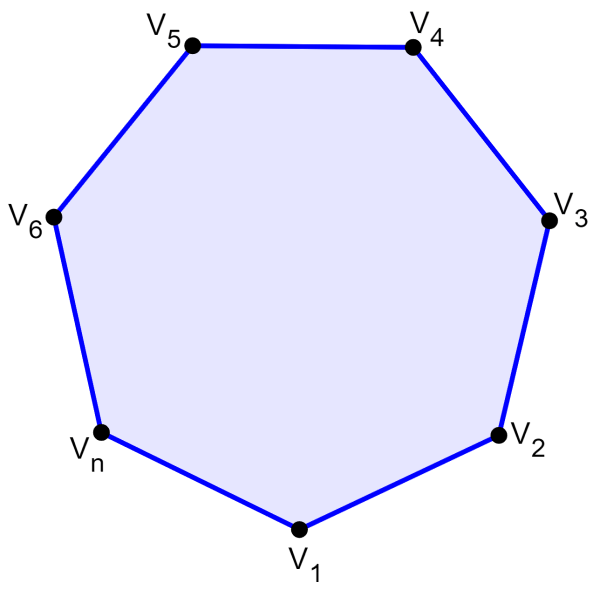
Podemos unir o vértice $latex V_{1}$ a todos os vértices, exceto $latex V_{2}$ e $latex V_{n}$. Então, vamos formar um $latex (n-2)$ número de triângulos, onde n é o número de lados do polígono.
Além disso, podemos usar o fato de que a soma dos ângulos internos de um triângulo é sempre igual a 180°. Então, para um polígono com n lados, a soma de todos os seus ângulos internos é igual a $latex (n-2)\times 180$°.
Exemplos de soma dos ângulos internos de um polígono
EXEMPLO 1
Encontre a soma dos ângulos internos de um polígono irregular com 11 lados.
Solução: A soma dos ângulos internos é a mesma independentemente de o polígono ser regular ou irregular. Então, basta usar a fórmula com $latex n=11$ e temos:
$latex (n-2)\times 180$°
$latex =(11-2)\times 180$°
$latex =(9)\times 180$°
$latex =1620$°
Um polígono irregular com 11 lados tem a soma dos ângulos internos de 1620°.
EXEMPLO 2
Encontre a medida dos ângulos individuais de um polígono regular de 9 lados.
Solução: Devemos começar calculando a soma dos ângulos internos do polígono. Então temos:
$latex (n-2)\times 180$°
$latex =(9-2)\times 180$°
$latex =(7)\times 180$°
$latex =1260$°
Agora, podemos dividir essa soma por 9, já que o polígono é regular:
1260°÷9=140°
Cada ângulo individual mede 140°
Veja também
Interessado em aprender mais sobre soma de ângulos internos de polígonos? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
