Um triângulo isósceles é um triângulo que consiste em dois lados iguais. Como esses triângulos têm dois lados iguais, isso também significa que eles têm dois ângulos iguais. Semelhante a outros triângulos, os triângulos isósceles têm três vértices, três arestas e seus ângulos internos somam 180°.
A seguir, conheceremos as características fundamentais dos triângulos isósceles. Além disso, veremos suas fórmulas mais importantes e as usaremos para resolver alguns exercícios.
GEOMETRIA
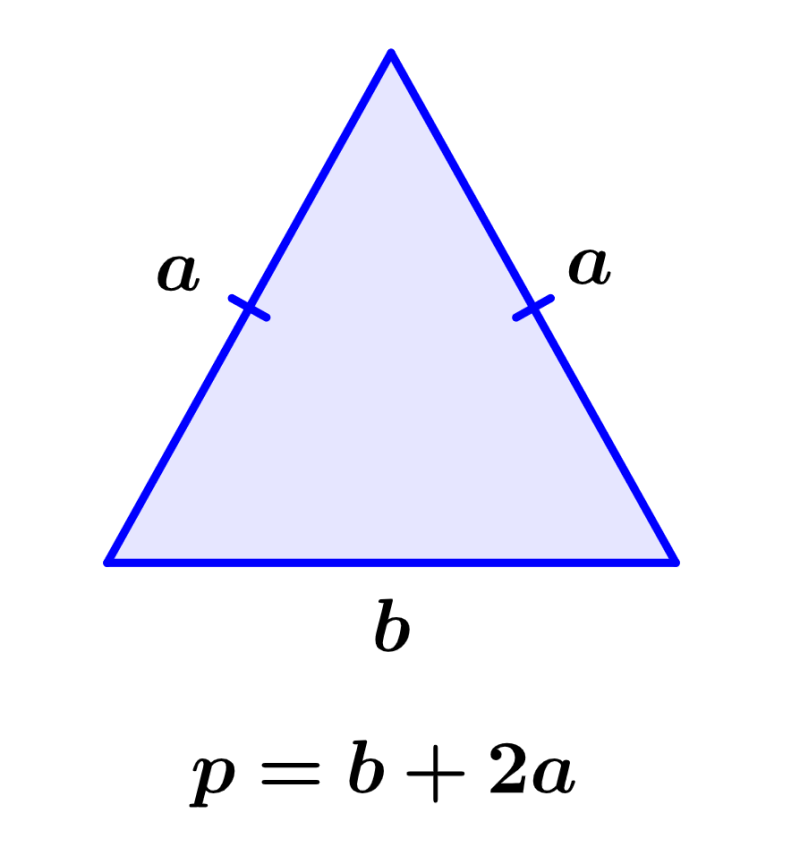
Relevante para…
Conhecer as características fundamentais dos triângulos isósceles.
GEOMETRIA
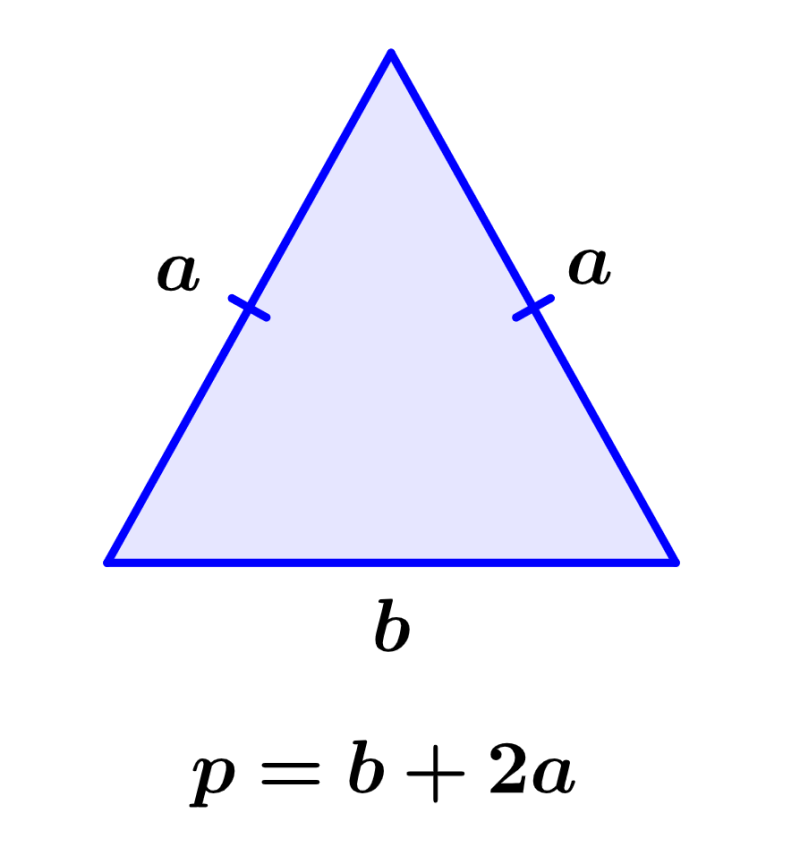
Relevante para…
Conhecer as características fundamentais dos triângulos isósceles.
Características fundamentais de triângulos isósceles
Um triângulo isósceles tem as seguintes características:
- Dois lados são congruentes entre si, ou seja, dois lados têm o mesmo comprimento.
- O terceiro lado de um triângulo isósceles, que é desigual com os outros dois lados, é chamado de base do triângulo isósceles.
- Os dois ângulos opostos aos lados iguais são congruentes entre si. Isso significa que ele tem dois ângulos de base congruentes.
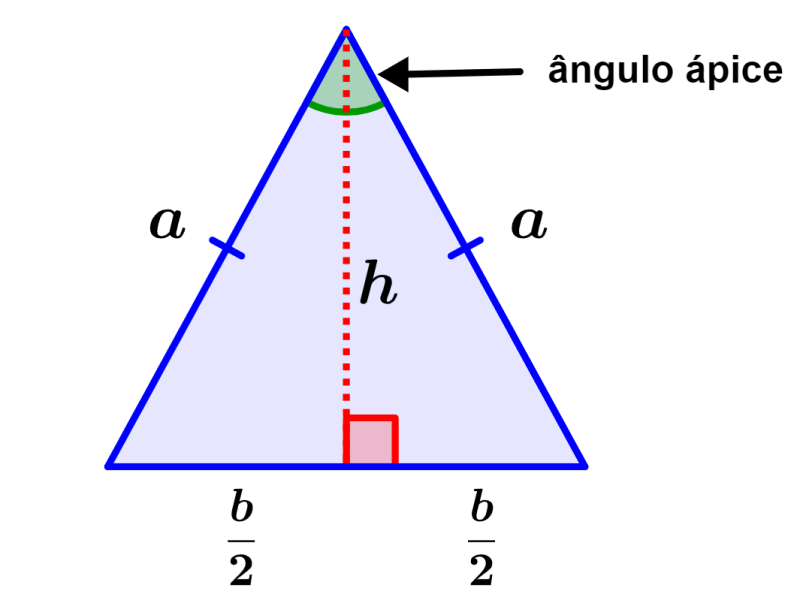
- O ângulo que não é congruente com os outros ângulos é denominado ângulo ápice.
- A altura do ângulo ápice de um triângulo isósceles divide a base em duas partes iguais e também divide o ângulo ápice em dois ângulos iguais.
- A altura do ângulo ápice divide o triângulo em dois triângulos retângulos.
Fórmulas importantes de triângulos isósceles
As fórmulas mais importantes para triângulos isósceles são as fórmulas de perímetro, altura e área.
Fórmula do perímetro do triângulo isósceles
O perímetro dos triângulos isósceles é calculado somando os comprimentos de todos os lados do triângulo. Nesse caso, dois dos comprimentos são iguais, então podemos usar a seguinte fórmula:
| $latex p=b+2a$ |
onde, b é o comprimento da base e a é o comprimento dos lados congruentes.
Fórmula da área do triângulo isósceles
A área de qualquer triângulo pode ser calculada multiplicando o comprimento da base pelo comprimento da altura e dividindo por 2. Portanto, temos:
| $latex A= \frac{1}{2} \times b \times h$ |
onde, b é o comprimento da base e h é o comprimento da altura.
Fórmula para a altura dos triângulos isósceles
Podemos calcular a altura dos triângulos isósceles usando os comprimentos dos lados do triângulo. Então, temos:
| $latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$ |
onde, a é o comprimento dos lados congruentes e b é o comprimento da base.
Exemplos de problemas de triângulos isósceles
EXEMPLO 1
- Qual é o perímetro de um triângulo isósceles com uma base de comprimento de 12 m e lados congruentes de comprimento de 8 m?
Solução: Temos os seguintes valores:
- Base, $latex b=12$ m
- Lados, $latex a=8$ m
Usando esses valores na fórmula do perímetro, temos:
$latex p=b+2a$
$latex p=12+2(8)$
$latex p=12+16$
$latex p=28$
O perímetro é de 28 m.
EXEMPLO 2
- Um triângulo isósceles tem uma base de 15 m e uma altura de 10 m. Qual é a sua área?
Solução: Reconhecemos os seguintes valores:
- Base, $latex b=15$ m
- Altura, $latex h=10$ m
Substituímos esses valores na fórmula para a área:
$latex A= \frac{1}{2}bh$
$latex A= \frac{1}{2}(15)(10)$
$latex A=75$
A área é de 75 m².
EXEMPLO 3
- Qual é a altura de um triângulo isósceles que tem uma base de comprimento de 8 m e lados congruentes de comprimento de 12 m?
Solução: Temos as seguintes informações:
- Base, $latex b=8$ m
- Lados, $latex a=12$ m
Substituímos esses valores na fórmula para a área:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{12}^2}- \frac{{{8}^2}}{4}}$
$latex h= \sqrt{144- \frac{64}{4}}$
$latex h= \sqrt{128}$
$latex h=11,3$
A altura do triângulo é de 11,3 m.
Exercícios de triângulo isósceles para resolver
Veja também
Você quer aprender mais sobre triângulos isósceles? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
