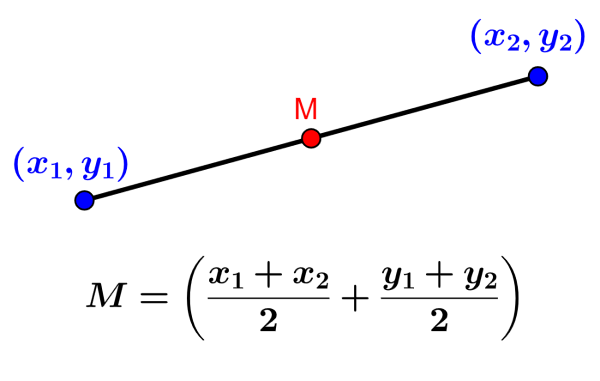
O ponto médio de um segmento representa o ponto que está localizado exatamente no meio das duas extremidades do segmento. O ponto médio pode ser encontrado dividindo a soma das coordenadas x por 2 e dividindo a soma das coordenadas y por 2.
A seguir, conheceremos a fórmula que podemos usar para calcular o ponto médio de um segmento. Além disso, usaremos essa fórmula para resolver alguns exercícios práticos.
O que é o ponto médio?
O ponto médio é um ponto localizado exatamente no meio de um segmento de linha que une dois pontos. Por exemplo, se temos dois pontos e os unimos com um segmento de reta, o ponto médio estará localizado no meio desse segmento e será equidistante de ambos os pontos.
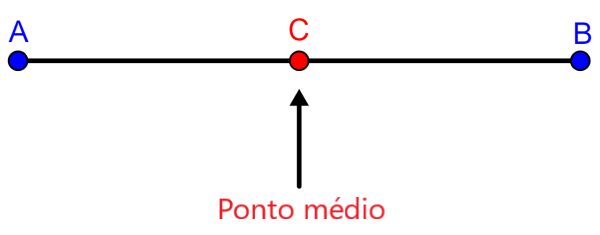
No diagrama abaixo temos os pontos A e B, unidos por um segmento. O ponto C é o ponto médio, pois está exatamente no meio do segmento. Para calcular a localização do ponto médio, basta medir o comprimento do segmento e dividir por 2.
Um ponto médio só pode ser calculado quando temos um segmento de reta unindo dois pontos, pois possui uma localização definida. O ponto médio não pode ser calculado para uma linha ou uma semi-reta, pois uma linha tem duas extremidades que se estendem indefinidamente e uma semi-reta tem uma extremidade que se estende indefinidamente.
Fórmula para o ponto médio de um segmento
A fórmula para o ponto médio de um segmento é derivada usando as coordenadas das extremidades do segmento. O ponto médio é igual a metade da soma das coordenadas x dos pontos e metade das coordenadas y dos pontos.
Então, se temos os pontos A e B com coordenadas $latex A=(x_{1}, y_{1})$ e $latex B=(x_{2}, y_{2})$, a fórmula do ponto médio é :
Fórmula do ponto médio
$$M=\left( \frac{x_{1}+x_{2}}{2}+\frac{y_{1}+y_{2}}{2}\right)$$
O ponto médio será expresso como as coordenadas $latex M=(x_{3}, y_{3})$.
Exercícios resolvidos de ponto médio de um segmento
EXERCÍCIO 1
Encontre o ponto médio de um segmento que une os pontos (2, 5) e (6, 9).
Solução
Temos as seguintes coordenadas
- $latex (x_{1}, y_{1})=(2, 5)$
- $latex (x_{2}, y_{2})=(6, 9)$
Agora, usamos a fórmula do ponto médio com as coordenadas fornecidas
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{2+6}{2},\frac{5+9}{2}\right)$$
$$=\left(\frac{8}{2},\frac{14}{2}\right)$$
$latex =\left(1, 7\right)$
O ponto médio é $latex M=(4, 7)$.
EXERCÍCIO 2
Qual é o ponto médio entre os pontos (2, 6) e (8, 12)?
Solução
Temos as seguintes coordenadas:
- $latex (x_{1}, y_{1})=(2, 6)$
- $latex (x_{2}, y_{2})=(8, 12)$
Usamos as coordenadas dadas na fórmula do ponto médio:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{2+8}{2},\frac{6+12}{2}\right)$$
$$=\left(\frac{10}{2},\frac{18}{2}\right)$$
$latex =(5, ~9)$
As coordenadas do ponto médio são $latex M=(5, ~9)$.
EXERCÍCIO 3
Qual é o ponto médio de um segmento de linha que une os pontos (4, 7) e (9, 10)?
Solução
Podemos escrever da seguinte forma:
- $latex (x_{1}, y_{1})=(4, 7)$
- $latex (x_{2}, y_{2})=(9, 10)$
Aplicando a fórmula do ponto médio com as coordenadas dadas, temos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{4+9}{2},\frac{7+10}{2}\right)$$
$$=\left(\frac{13}{2},\frac{17}{2}\right)$$
O ponto médio é $latex M=\left(\frac{13}{2},\frac{17}{2}\right)$.
EXERCÍCIO 4
Determina o ponto médio entre os pontos (5, 7) e (9, 13).
Solução
Temos os seguintes pontos:
- $latex (x_{1}, y_{1})=(5, 7)$
- $latex (x_{2}, y_{2})=(9, 13)$
Aplicamos a fórmula do ponto médio com estes pontos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{5+9}{2},\frac{7+13}{2}\right)$$
$$=\left(\frac{14}{2},\frac{20}{2}\right)$$
$latex =(7,~10)$
As coordenadas do ponto médio são $latex M=(7, ~10)$.
EXERCÍCIO 5
Se tivermos os pontos (-4, -2) e (6, 5) conectados por um segmento de reta, qual é o seu ponto médio?
Solução
Temos os seguintes valores:
- $latex (x_{1}, y_{1})=(-4, -2)$
- $latex (x_{2}, y_{2})=(6, 5)$
Neste caso, temos coordenadas negativas, porém, simplesmente aplicamos a fórmula do ponto médio como nos exercícios anteriores:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{-4+6}{2},\frac{-2+5}{2}\right)$$
$$=\left(\frac{2}{2},\frac{3}{2}\right)$$
$$=\left(1,\frac{3}{2}\right)$$
O ponto médio tem as coordenadas $latex M=\left(1,\frac{3}{2}\right)$.
EXERCÍCIO 6
Encontre o ponto médio se tivermos os pontos (-5, -6) e (6, -2).
Solução
Escrevemos as coordenadas da seguinte forma:
- $latex (x_{1}, y_{1})=(-5, -6)$
- $latex (x_{2}, y_{2})=(6, -2)$
Neste caso, temos coordenadas negativas, mas simplesmente usamos a fórmula do ponto médio como nos exercícios anteriores:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{-5+6}{2},\frac{-6-2}{2}\right)$$
$$=\left(\frac{1}{2},\frac{-8}{2}\right)$$
$$=\left(\frac{1}{2}, -4\right)$$
O ponto médio tem as coordenadas $latex M=\left(\frac{1}{2},~ -4\right)$.
EXERCÍCIO 7
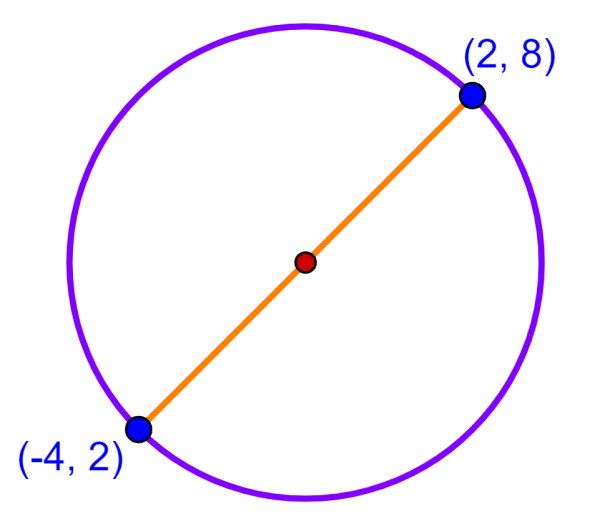
O diâmetro de um círculo tem extremidades (-4, 2) e (2, 8). Quais são as coordenadas do centro do círculo?
Solução
O centro do círculo divide o diâmetro em duas partes iguais. Isso significa que, para encontrar o centro, temos que encontrar as coordenadas do ponto médio do diâmetro. Então, começamos com as coordenadas:
- $latex (x_{1}, y_{1})=(-4,2)$
- $latex (x_{2}, y_{2})=(2,8)$
Agora, aplicamos a fórmula do ponto médio com estas coordenadas:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{-4+2}{2},\frac{2+8}{2}\right)$$
$$=\left(\frac{-2}{2},\frac{10}{2}\right)$$
$latex =(-1,5)$
As coordenadas do centro do círculo são $latex (-1, 5)$.
EXERCÍCIO 8
As extremidades de um segmento são (p, 4) e (8, 10). Encontre o valor de p se o ponto médio for (3, 7).
Solução
Escrevemos as coordenadas dadas:
- $latex (x_{1}, y_{1})=(p, 4)$
- $latex (x_{2}, y_{2})=(8, 10)$
Agora, podemos aplicar a fórmula do ponto médio com os valores conhecidos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{p+8}{2},\frac{4+10}{2}\right)$$
Neste caso, precisamos encontrar o valor de p que faz parte das coordenadas x do ponto médio. Então, consideramos a componente x, formamos uma equação e resolvemos p. Sabemos que a coordenada x do ponto médio é 3, então temos
$$3=\left(\frac{p+8}{2}\right)$$
$latex 6=p+8$
$latex p=-2$
O valor de p é -2.
EXERCÍCIO 9
Se o ponto médio de um segmento é (-2, 1) e os seus pontos finais são (-6, q) e (2, 4), qual é o valor de q?
Solução
Temos as seguintes coordenadas:
- $latex (x_{1}, y_{1})=(-6, x)$
- $latex (x_{2}, y_{2})=(2, -4)$
Quando aplicamos a fórmula do ponto médio, temos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{-6+2}{2},\frac{q+4}{2}\right)$$
Para encontrar o valor de q, formamos uma equação com a coordenada y do ponto médio:
$$\left(\frac{q+4}{2}\right)=1$$
$latex q+4=2$
$latex q=-2$
O valor de q é -2.
EXERCÍCIO 10
O ponto médio de um segmento tem coordenadas (-3, -4). Se os pontos finais do segmento forem (3, -1) e (m, -7), encontrar o valor de m.
Solução
Começamos com as seguintes coordenadas:
- $latex (x_{1}, y_{1})=(3, -1)$
- $latex (x_{2}, y_{2})=(m, -7)$
Aplicando a fórmula do ponto médio, temos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{3+m}{2},\frac{-1-7}{2}\right)$$
À semelhança dos exercícios anteriores, só temos de considerar as coordenadas-x do ponto médio e formar uma equação:
$$\left(\frac{3+m}{2}\right)=-3$$
$latex 3+m=-6$
$latex m=-9$
O valor de m é -9.
Exercícios de ponto médio de um segmento para resolver
Um segmento é definido pelos pontos (p, 3) e (5, 13). Se o ponto médio é (1, 8), qual é o valor de p?
Escreva a resposta na caixa.
Veja também
Interessado em aprender mais sobre ponto médio e distância no plano? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
