Os polígonos em estrela são formados quando estendemos os lados de um polígono e esses lados se cruzam. O número de vezes que os lados se cruzam fora do polígono determina o grau do polígono estrela.
A seguir, aprenderemos mais detalhes sobre polígonos de estrelas. Usaremos diagramas e vários exemplos para entender os conceitos.
Processo de estrelação
A estrelação é o processo de construção de poliedros estendendo os lados dos polígonos até que eles se cruzem. Se os lados nunca se cruzam em um ponto fora do polígono, o polígono não pode ser estelar.
Por exemplo, a estrela de um hexágono regular é mostrada na imagem abaixo.
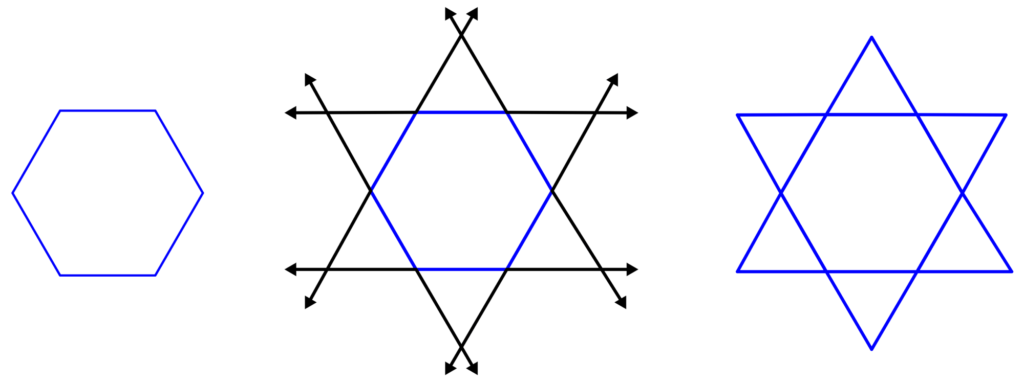
Agora, vamos pensar em qual dos seguintes polígonos não pode ser estrelado:
• Quadrado
• Pentágono regular
• Octógono regular
• Decágono regular
A resposta é um quadrado. Ao estender os lados de um quadrado, formamos linhas paralelas que nunca se cruzam em um ponto.
Estelações de ordem n
Uma estrelação de primeira ordem de um polígono estende os lados até que as linhas se cruzem primeiro fora do polígono. Uma estrela de ordem n estende os lados de um polígono até que as linhas se cruzem n vezes em cada direção.
Por exemplo, o diagrama a seguir mostra uma estrelação de segunda ordem, já que as linhas que saem do polígono se cruzam duas vezes.
Podemos determinar a medida do ângulo x usando o seguinte diagrama:
Como o octógono é regular, os ângulos internos do octógono medem 135°. Então, no diagrama temos que a=135°. Como a e b são um par linear, b=180°-135°=45°. Isso implica que cada triângulo na estrela é um triângulo retângulo isósceles, com ângulos retos.
Os ângulos de um quadrilátero somam 360°, então y=360°-90°-90°-135°=45°.
Finalmente, como y e x são um par linear, temos x=180°-45°=135°.
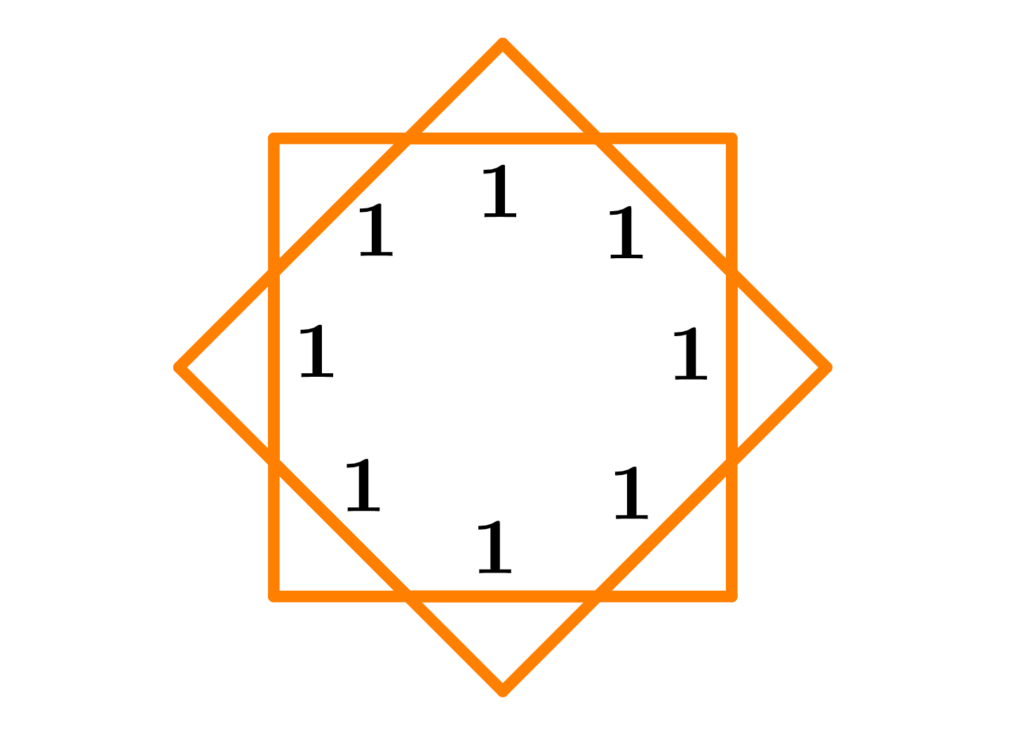
Agora, vamos ver outras maneiras de formar polígonos de estrelas. Se começarmos com um quadrado e depois colocarmos um quadrado congruente girado em 45°, geraremos um octógono estelar de primeira ordem.
Se começarmos com um triângulo equilátero e colocarmos várias cópias giradas em 30°, formaremos um dodecágono (12 lados). Se girarmos 30°, após 120° de rotação, o triângulo estará sobrepondo-se ao triângulo original. Isso significa que existem (120°)/(30°)=4 triângulos equiláteros, que formam um polígono com 3×4=12 lados.
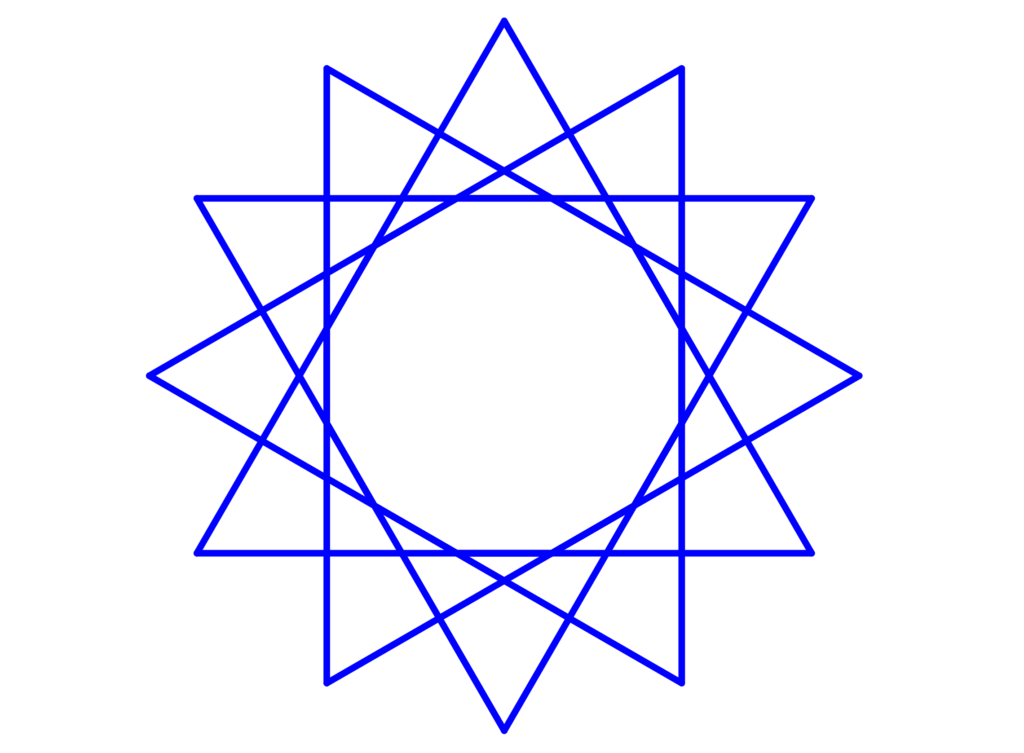
A figura é um polígono estelar de terceira ordem, pois as pontas dos triângulos estão na terceira interseção.
Exemplos de polígono estrela
EXEMPLO 1
A imagem abaixo é um polígono regular com área A, e esse mesmo hexágono é estrelado para formar uma estrela. Qual é a área da estrela?
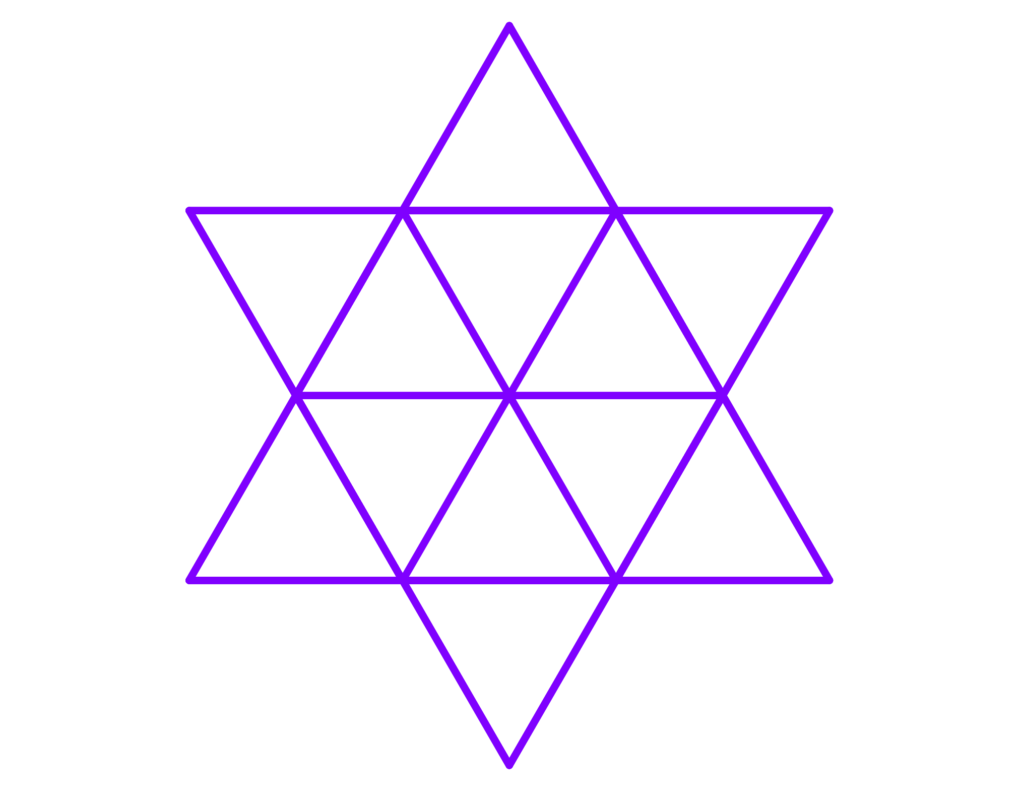
Solução: Um hexágono regular pode ser dividido em triângulos equiláteros. Todos os ângulos serão de 60°.
As estrelas também são triângulos equiláteros. Como cada ângulo do hexágono regular original é $latex \frac{((6-2)180^{\circ})}{6}=120$°, os ângulos dos triângulos externos devem ser 180°-120°= 60°.
Como os triângulos são iguais, a área do pentágono original e a soma das áreas dos triângulos externos são iguais. Portanto, a área total é 2A.
EXEMPLO 2
Que fração da área total do pentágono estrelado a região verde representa?
Solução: Cada parte da figura na região verde tem uma parte congruente na região branca. Essas peças estão marcadas na figura.
Por causa disso, a área da região verde é exatamente metade da área de toda a figura.
EXEMPLO 3
Um octógono regular com perímetro de 8 unidades é estrelado para formar uma estrela como mostra a imagem abaixo. Qual é o perímetro da estrela?
Solução: 8√2
Como o octógono é regular, cada um dos triângulos externos é um triângulo retângulo isósceles com hipotenusa de 8/8 = 1.
Os lados da estrela são congruentes. Podemos usar x para representar o comprimento de seus lados e usando o teorema de Pitágoras, temos:
$latex {{x}^2}+{{x}^2}={{1}^2}$
$latex {{2x}^2}=1$
$latex {{x}^2}=\frac{1}{2}$
$latex x=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$
Como a estrela tem 16 lados, isso significa que o perímetro é $latex 16\times \frac{\sqrt{2}}{2}=8\sqrt{2}$.
Veja também
Quer saber mais sobre figuras geométricas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
