Figuras semelhantes são caracterizadas por terem sempre a mesma forma, mas não o mesmo tamanho. Essas figuras têm ângulos iguais, mas não lados iguais. As razões dos lados correspondentes de figuras semelhantes são chamadas de fator de escala e podem ser usadas para descrever quão grande ou quão pequena uma figura é comparada a outra.
A seguir, aprenderemos sobre figuras semelhantes e seus fatores de escala com mais detalhes.
Definição de figuras semelhantes
Duas ou mais figuras são consideradas semelhantes quando têm a mesma forma. Figuras semelhantes podem ter o mesmo tamanho ou uma pode ser maior que a outra.
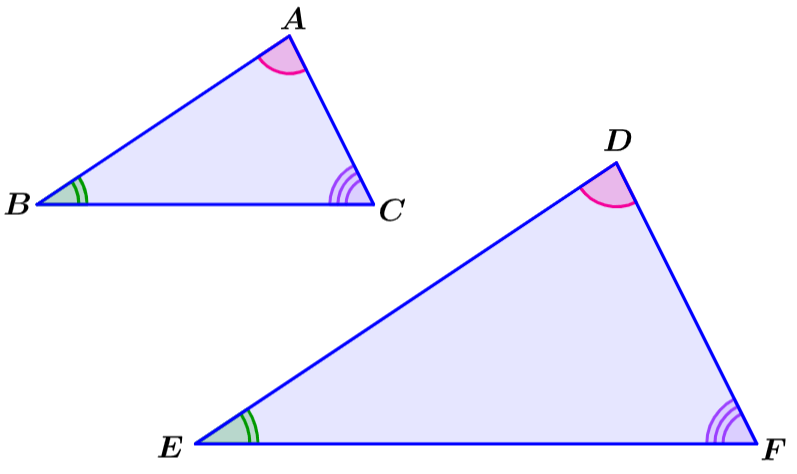
Usamos o símbolo «~» para indicar que duas figuras são semelhantes. Por exemplo, se os triângulos ABC e DEF são semelhantes, podemos escrever:
ΔABC ~ ΔDEF
Como a forma de figuras semelhantes é a mesma, seus ângulos correspondentes também serão os mesmos. Podemos usar a declaração de similaridade para determinar quais ângulos são iguais.
Por exemplo, no exemplo acima, os ângulos A e D são iguais, pois são escritos em primeira ordem. Da mesma forma, os ângulos B e E também são iguais, assim como os ângulos C e F.
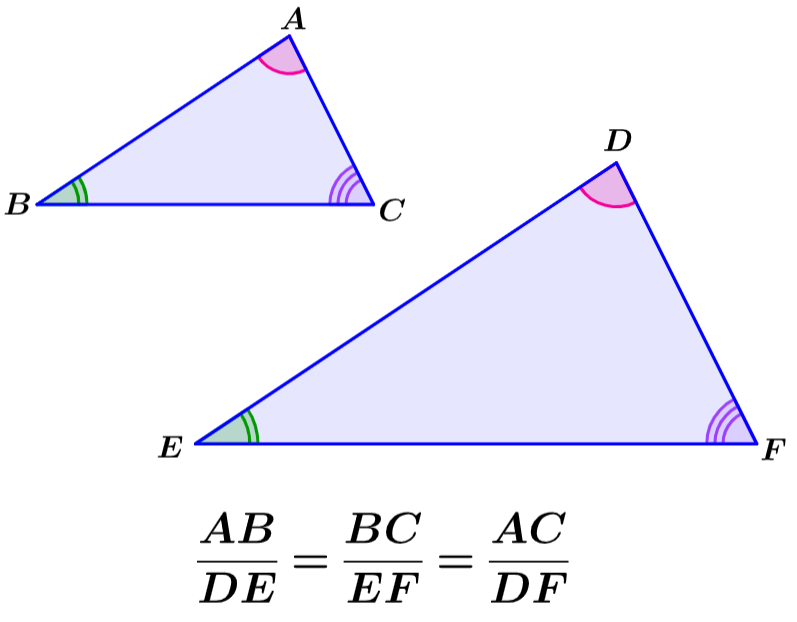
Figuras semelhantes podem ter lados de tamanhos diferentes, portanto, os comprimentos correspondentes não são necessariamente os mesmos. No entanto, as proporções dos ângulos correspondentes são sempre as mesmas. Por exemplo, nas seguintes figuras semelhantes, temos as proporções:
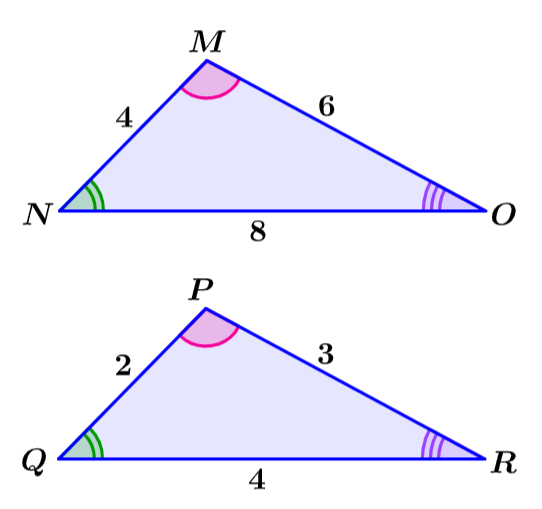
Agora, se dividirmos todos os lados correspondentes das figuras semelhantes a seguir, sempre obteremos 1/2. Para que duas figuras sejam semelhantes, as proporções de seus lados correspondentes devem ser as mesmas.
O que são fatores de escala?
Os fatores de escala são as razões que obtemos quando dividimos os comprimentos dos lados correspondentes de figuras semelhantes. No exemplo acima, todas as razões são simplificadas para 1/2, então o fator de escala do triângulo ABC para o triângulo DEF é 1/2.
Também podemos pensar em fatores de escala como multiplicadores. Por exemplo, o fator de escala do triângulo MNO ao triângulo PQR é 2. Isso significa que o triângulo PQR é duas vezes maior que o triângulo MNO.
Se multiplicarmos um lado do triângulo MNO por 2, obtemos o comprimento do lado correspondente do triângulo PQR. As razões de todos os lados desses triângulos são iguais a 2. Ou seja, temos $latex \frac{10}{5}=2$, $latex \frac{12}{6}=2$, $latex \frac{6}{3}=2$.
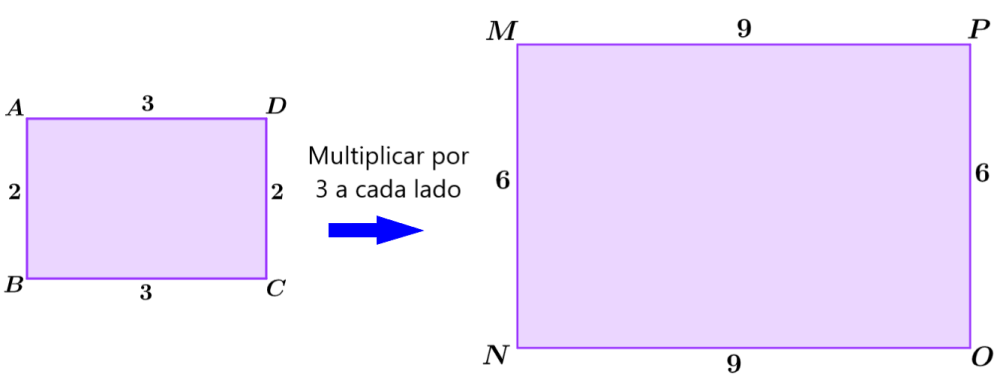
Vejamos outro exemplo. O fator de escala do retângulo ABCD ao retângulo MNOP é 3. Isso significa que o segundo retângulo é três vezes maior em comparação com o primeiro retângulo. Podemos obter os comprimentos dos lados correspondentes do segundo retângulo multiplicando os lados do primeiro retângulo por 3.
Exemplos de fatores de escala
EXEMPLO 1
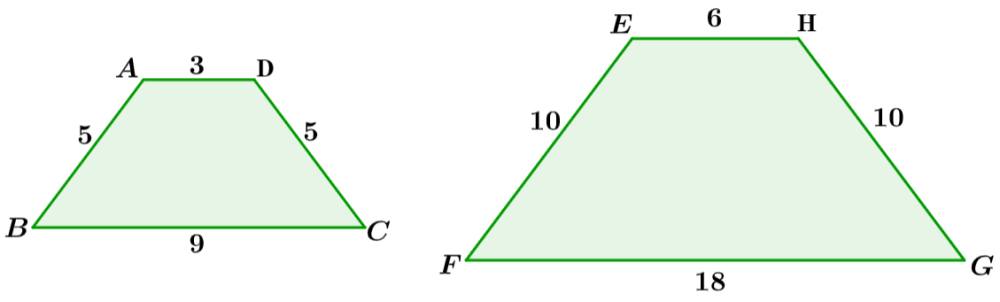
Encontre o fator de escala do trapézio ABCD para o trapézio EFGH.
Solução: Neste caso, a figura pequena foi indicada primeiro. Como o segundo número é maior, isso significa que o fator de escala deve ser maior que 1.
Agora, comparando os comprimentos dos lados correspondentes, podemos deduzir que podemos multiplicar por 2 para obter os mesmos comprimentos. Portanto, o fator de escala é 2. Também podemos encontrar o fator de escala encontrando as seguintes razões:
$latex \frac{6}{3}=2, ~\frac{10}{5}=2, ~\frac{18}{9}=2$
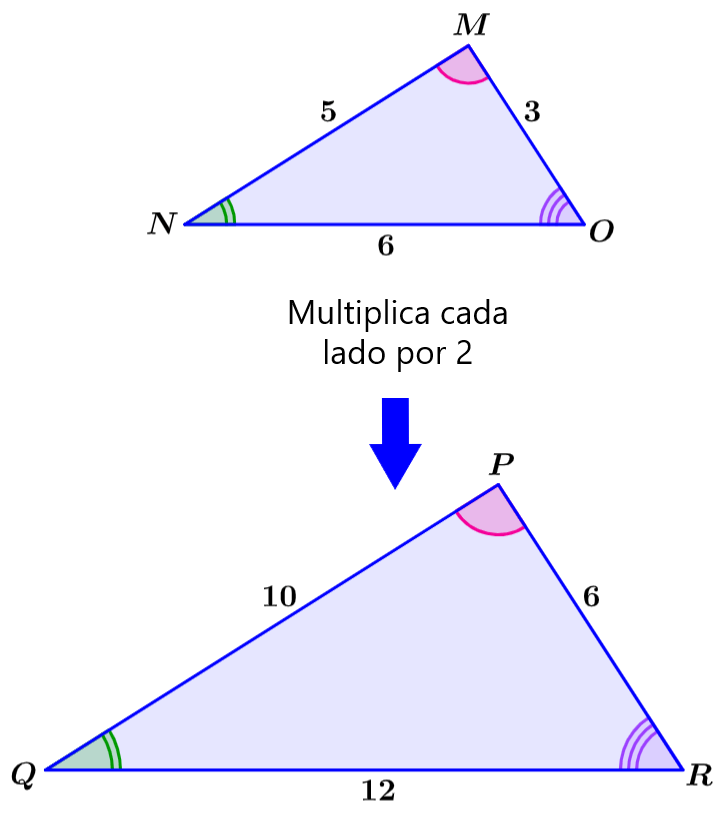
EXEMPLO 2
Encontre o fator de escala do triângulo MNO ao triângulo PQR
Solução: O segundo triângulo indicado é maior que o primeiro, então sabemos que o fator de escala será maior que 1. Neste caso, o fator de escala não é um inteiro, então não podemos determiná-lo à vista.
Assim, podemos encontrar as proporções dos lados correspondentes.
Sabemos que o fator de escala é maior que 1, então colocamos o número maior no numerador das frações. Assim, temos as proporções:
$latex \frac{8}{4}=2,~\frac{10}{5}=2, ~\frac{6}{3}=2$
Portanto, o fator de escala é 2.
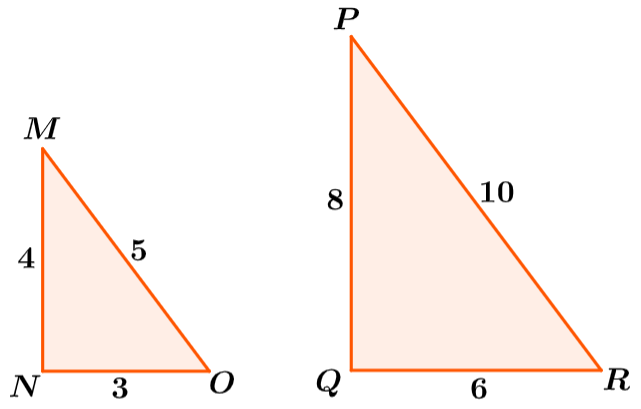
EXEMPLO 3
Encontre o fator de escala do triângulo PQR ao triângulo MNO.
Solução: Este exemplo é semelhante ao exemplo anterior, exceto que a ordem é alterada. Como o segundo triângulo é menor, o fator de escala será menor que 1 neste caso.
Sabemos que a ordem foi simplesmente alterada, então podemos inverter as frações para encontrar as proporções corretas:
$latex \frac{4}{8}=\frac{1}{2}, ~\frac{3}{6}=\frac{1}{2}, \frac{5}{10}=\frac{1}{2}$
Então, o fator de escala é $latex \frac{1}{2}$.
Veja também
Quer saber mais sobre figuras geométricas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
