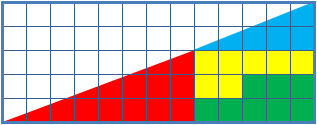
O paradoxo do quadrado perdido é uma ilusão ótica encontrada na matemática, que é usada para aprender a raciocinar usando os axiomas da geometria e descrições textuais em vez de simplesmente confiar em figuras geométricas. O paradoxo é composto por dois triângulos retângulos com dimensões 13×5, mas um dos triângulos tem um quadrado oco de 1×1.
A seguir, aprenderemos sobre a solução para esse paradoxo.
Paradoxo do quadrado perdido
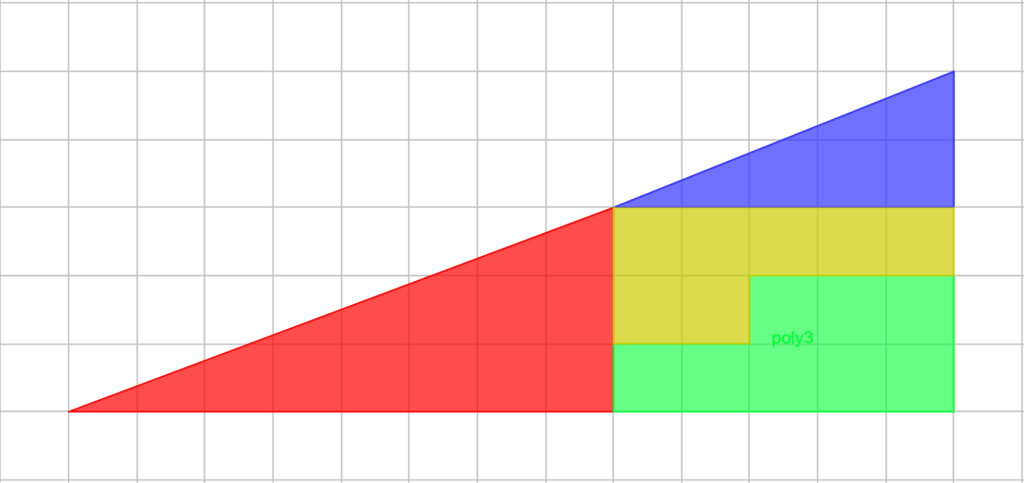
Na imagem acima temos um triângulo com dimensões 13×5 que é formado por 4 polígonos. Se reorganizarmos os polígonos, obtemos a seguinte figura:
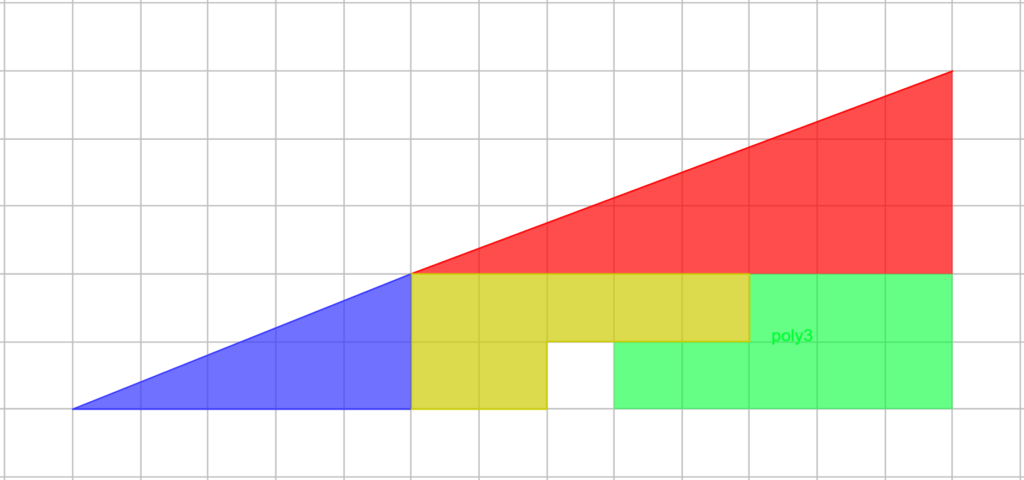
Ambas as figuras são compostas pelos mesmos 4 polígonos, mas podemos ver que a segunda figura tem um quadrado 1×1 ausente.
Ambas as figuras têm uma altura de 5 unidades e uma base de 15. A área de um triângulo pode ser calculada usando a fórmula A=1/2 bh, onde b é o comprimento da base e h é a altura do triângulo. Então temos:
A=1/2×13×5=32,5
Solução para o paradoxo do quadrado perdido
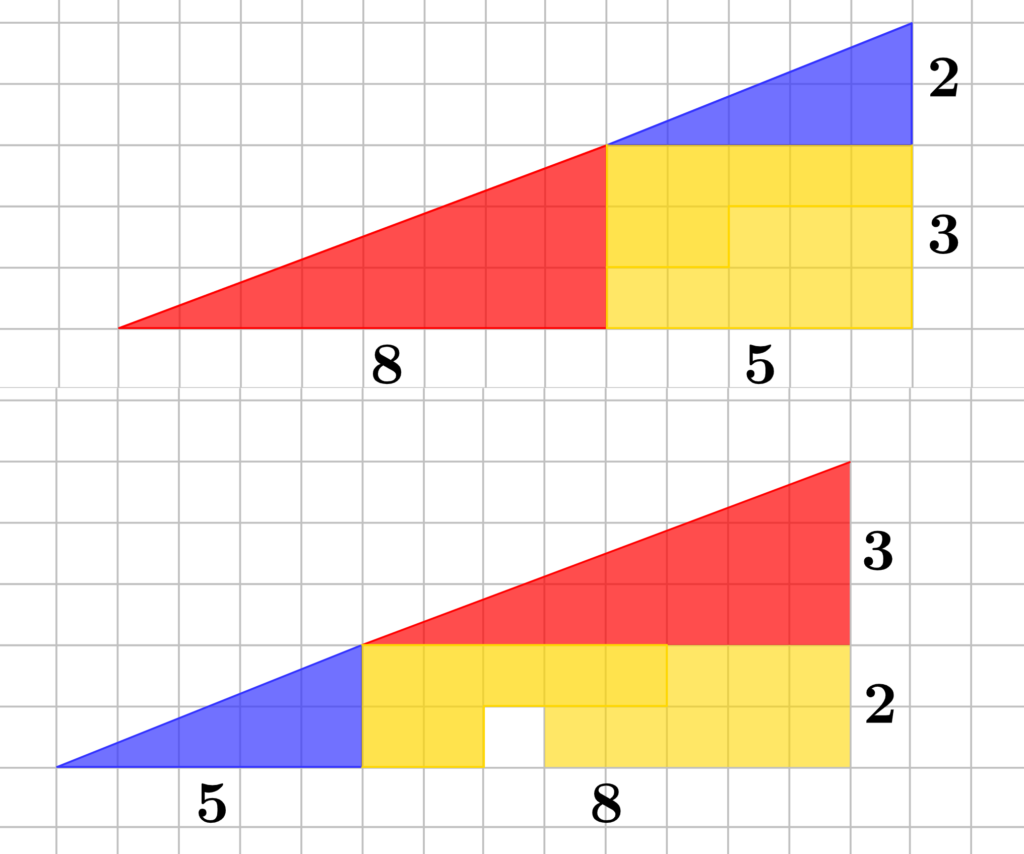
Para encontrar a solução para esse paradoxo, podemos começar determinando a área de cada um dos polígonos que compõem a figura a seguir:
As áreas dos triângulos podem ser calculadas usando A=1/2 bh e as áreas das outras figuras podem ser calculadas dividindo-as em retângulos ou simplesmente contando o número de quadrados em cada figura.
A área do triângulo azul é 1/2×5×2=5.
A área do triângulo vermelho é 1/2×8×3=12.
A área do polígono amarelo é 7.
A área do polígono verde é 8.
A área total dessas figuras é 32. Observe que isso é menor que a área do triângulo com dimensões 13×5. A área de todos os polígonos na figura acima é igual a 32, no entanto, a área do triângulo com dimensões 13×5 é 32,5.
Isso nos diz que estamos cometendo um erro em algum lugar, já que a área das formas não pode mudar do nada.
Agora, vamos calcular os declives das hipotenusas dos triângulos azul e vermelho separadamente e depois somá-las.
A altura do triângulo vermelho é 3 e o comprimento de sua base é 8, então o declive do triângulo vermelho é 3/8.
A altura do triângulo azul é 2 e o comprimento de sua base é 5, então o declive do triângulo azul é 2/5.
Somando esses declives, temos 3/8+2/5=31/40.
Os declives dos triângulos azul e vermelho não são os mesmos. Isso significa que a hipotenusa da figura não é uma linha reta, o que significa que as figuras não são triângulos. A Figura 1 tem um declive que se curva ligeiramente para dentro e a Figura 2 tem um declive que se curva levemente para fora. Comparando esses números, vemos que as hipotenusas não coincidem.
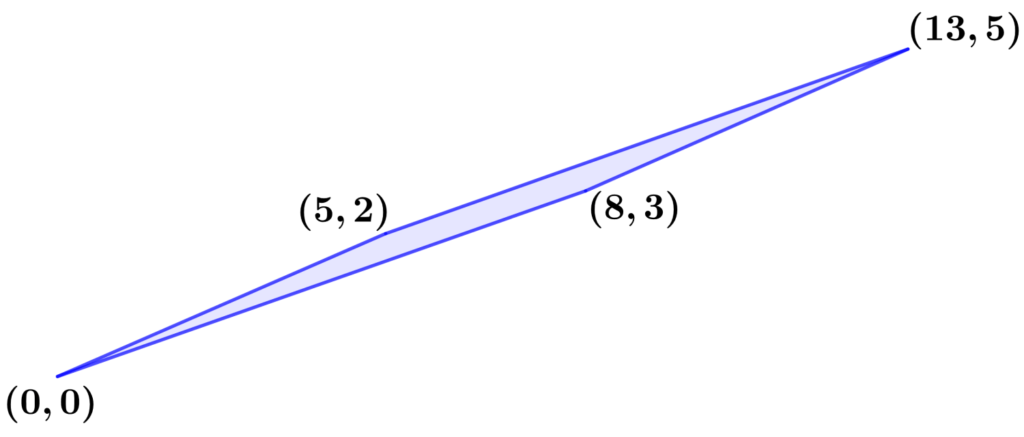
Paradoxo do quadrado perdido e números de Fibonacci
Vimos que nenhuma das figuras é realmente um triângulo e a diferença entre suas áreas é exatamente 1.
Podemos fazer a observação de que os comprimentos dos lados dos polígonos que formam as figuras, 2, 3, 5 e 8, são números de Fibonacci sucessivos.
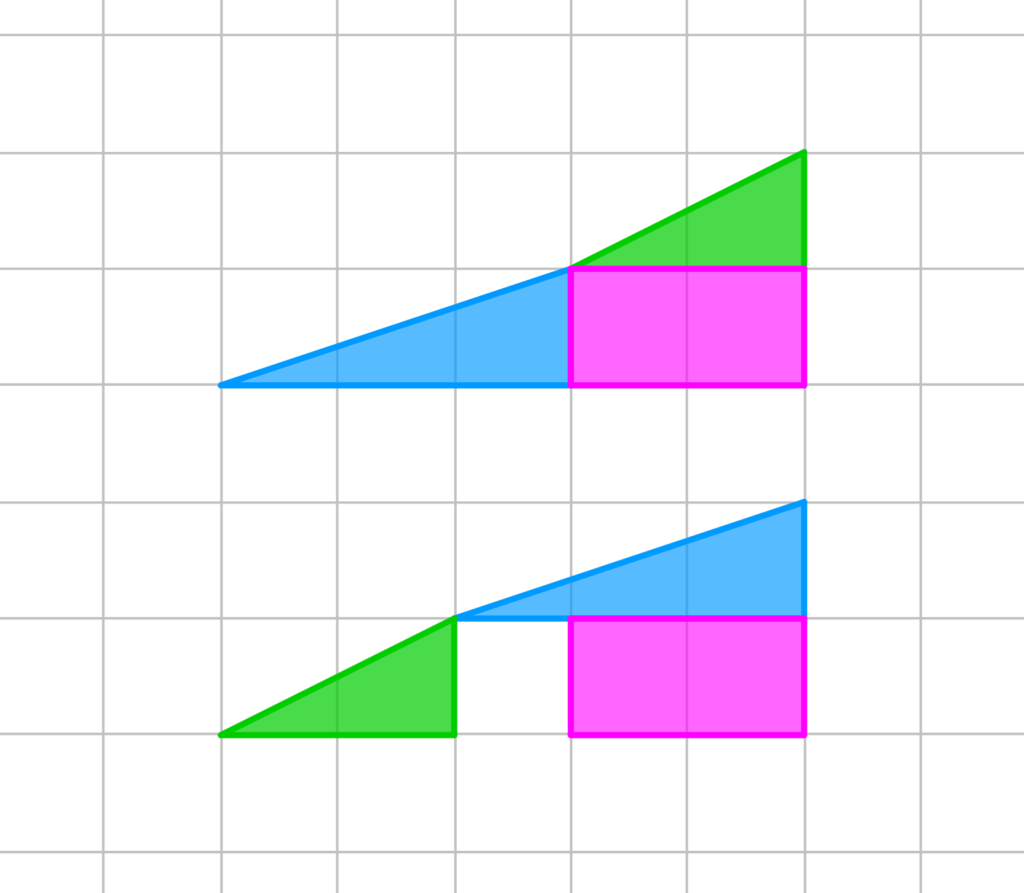
Acontece que podemos recriar o paradoxo do quadrado ausente usando 4 números consecutivos de Fibonacci para construir os triângulos de maneira análoga. Por exemplo, nas figuras abaixo temos os números de Fibonacci 1, 1, 2, 3. Podemos reorganizar o retângulo para criar um buraco de área 1. Porém, desta vez a ilusão é menos convincente, pois os declives são visivelmente diferentes.
Veja também
Quer saber mais sobre figuras geométricas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
