A desigualdade triangular é um dos teoremas mais conhecidos da geometria. Este teorema nos diz que a soma de dois dos lados do triângulo é maior que o terceiro lado do triângulo. Se tivermos um segmento maior que a soma dos outros dois segmentos, não podemos formar um triângulo.
A seguir, aprenderemos mais detalhes sobre a desigualdade triangular junto com alguns exemplos.
O que é a desigualdade triangular?
A desigualdade triangular é um teorema que afirma que em qualquer triângulo, a soma de dois dos três lados do triângulo deve ser maior que o terceiro lado. Por exemplo, no diagrama a seguir, temos o triângulo ABC:
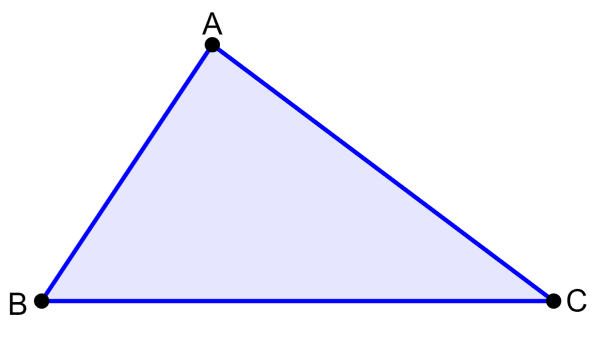
A desigualdade triangular nos diz que:
- A soma AB+BC deve ser maior que AC. Então, temos AB+BC>AC.
- A soma AB+AC deve ser maior que BC. Então, temos AB+AC>BC.
- A soma BC+AC deve ser maior que AB. Então, temos BC+AC>AB.
Podemos entender a desigualdade triangular imaginando que estamos caminhando ao longo dos lados do triângulo ABC. Se tivermos que ir do ponto A ao ponto B, o caminho mais curto é a linha reta AB. Se formos primeiro para C e depois para B, a distância que percorremos, AC+CB, com certeza será maior que AB.
Se a soma dos dois lados não fosse maior que o terceiro lado, não poderíamos formar um triângulo, pois um dos segmentos seria muito curto para conectar os outros dois.
Prova da desigualdade triangular
Podemos obter uma prova da desigualdade triangular considerando o seguinte triângulo ABC:
Vamos provar que AB+AC>BC. Em seguida, estendemos o segmento BA até o ponto D, de forma que temos os segmentos AD=AC. Em seguida, conectamos os pontos C e D conforme mostrado no diagrama:
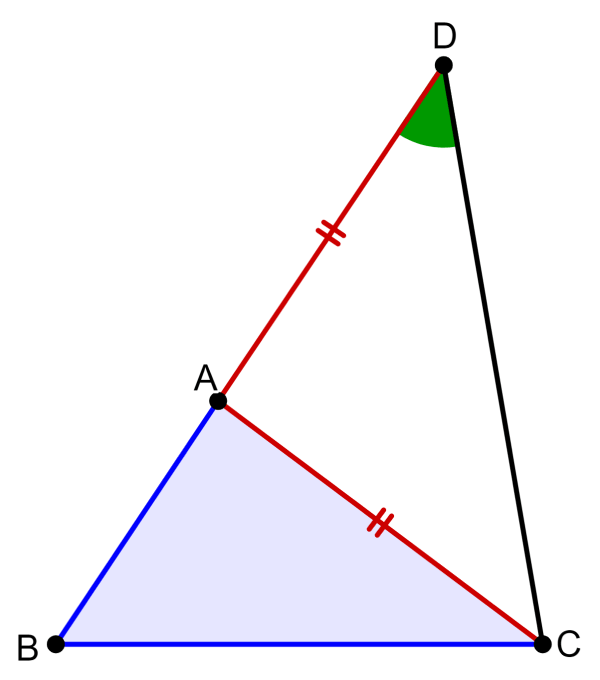
Podemos ver que os ângulos ∠ACD e ∠D são iguais. Isso significa que no triângulo BCD, temos ∠BCD > ∠D. Além disso, sabemos que os lados opostos a grandes ângulos também são grandes, então temos BD>BC.
O segmento BD é igual a AB+AD. Então, temos AB+AD>BC. Finalmente, sabemos que AD=AC, então temos:
AB+AC>BC
Desigualdade de triângulos com vetores
No diagrama a seguir, temos um triângulo formado pelos vetores $latex \vec{a}$,$latex \vec{b}$ e $latex \vec{a}+\vec{b}$.
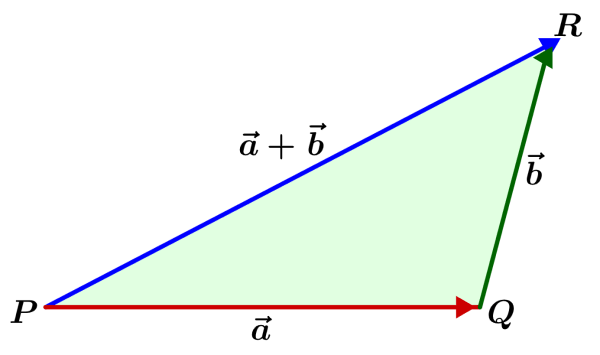
Sabemos que em um triângulo, a soma de dois lados é sempre maior que o terceiro lado. No triângulo acima, temos $latex PQ=|\vec{a}|$, $latex QR=|\vec{b}|$ e $latex PR=|\vec{a}+\vec{b}| $. Então temos:
$latex |\vec{a}+\vec{b}|<|\vec{a}|+\vec{b}|$
Além disso, também sabemos que a diferença de dois lados é menor que o terceiro lado. Então temos:
$latex |\vec{a}|-|\vec{b}|<|\vec{a}+\vec{b}|$
Combinando essas duas desigualdades, temos:
$latex |\vec{a}|-|\vec{b}|<|\vec{a}+\vec{b}|<|\vec{a}|+\vec{b}|$
Problemas resolvidos de desigualdade triangular
EXERCÍCIO 1
Determine se é possível formar um triângulo com três segmentos de comprimento 8 unidades, 6 unidades e 5 unidades.
Solução: Podemos começar atribuindo os valores a=8, b=6 e c=5. Então temos:
a+b>c
⇒ 8+6>5
⇒ 14>5 (é verdadeiro)
a+c>b
⇒ 8+5>6
⇒ 13>6 (é verdadeiro)
b+c>a
⇒ 6+5>8
⇒ 11>8 (é verdadeiro)
Como todas as condições são verdadeiras, é possível formar um triângulo com as medidas dadas.
EXERCÍCIO 2
É possível formar um triângulo com segmentos que tenham comprimentos de 12 unidades, 6 unidades e 5 unidades?
Solução: Novamente, atribuímos os valores a=12, b=6 e c=5. Então temos:
a+b>c
⇒ 12+6>5
⇒ 18>5 (é verdadeiro)
a+c>b
⇒ 12+5>6
⇒ 17>6 (é verdadeiro)
b+c>a
⇒ 6+5>12
⇒ 11>12 (não é verdade)
Uma das condições não é verdadeira, então não podemos formar um triângulo com essas medidas.
Veja também
Interessado em aprender mais sobre triângulos e a desigualdade triangular? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
