A área da superfície de uma esfera é a região coberta por sua superfície externa. Por outro lado, o volume representa o espaço tridimensional ocupado pela figura. Podemos calcular a área superficial de uma esfera usando a fórmula A=4πr² e podemos calcular seu volume usando a fórmula V=(4/3)πr³, onde r é o raio da esfera.
A seguir, aprenderemos tudo sobre a área e o volume de uma esfera. Vamos conhecer suas fórmulas e usá-las para resolver alguns exercícios práticos.
Como calcular a área de uma esfera?
Podemos calcular a área de uma esfera multiplicando o produto de pi pelo quadrado do raio da esfera por 4. Assim, a fórmula para a área da superfície de uma esfera é dada por:
| $latex A_{s}=4\pi{{r}^2}$ |
onde, $latex A_{s}$ representa a área da superfície da esfera e r representa o comprimento do raio.
Calcule a área de uma esfera usando o diâmetro
Se soubermos o comprimento do diâmetro, podemos calcular sua área usando dois métodos principais. O primeiro método é dividir o comprimento do diâmetro por 2 e, assim, usar a fórmula padrão para a área de uma esfera.
O segundo método é encontrar uma fórmula para a área de uma esfera em termos de diâmetro. Assim, substituindo a expressão r=d/2 na fórmula da área, temos:
$latex A_{s}=4\pi{{r}^2}$
$latex A_{s}=4\pi(\frac{d}{2})^2$
$latex A_{s}=4\pi(\frac{d^2}{4})$
| $latex A_{s}=\pi{{d}^2}$ |
Como calcular o volume de uma esfera?
Podemos calcular o volume de uma esfera usando a seguinte fórmula:
| $latex V=\frac{4}{3}\pi {{r}^3}$ |
onde r é o comprimento do raio da esfera.
A fórmula para o volume de uma esfera pode ser provada usando o cálculo integral.
Calcular o volume de uma esfera usando o diâmetro
Para calcular o volume de uma esfera usando seu diâmetro, podemos usar dois métodos diferentes. O primeiro método é dividir o diâmetro por 2 para obter o raio e usar a fórmula padrão para o volume de uma esfera.
O segundo método é obter uma fórmula para o volume de uma esfera em termos de diâmetro. Podemos fazer isso substituindo a expressão r = d/2 na fórmula do volume. Então nós temos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(\frac{d}{2})}^3}$
$latex V=\frac{4}{3}\pi (\frac{{{d}^3}}{8})$
$latex V=\frac{4}{24}\pi {{d}^3}$
| $latex V=\frac{1}{6}\pi {{d}^3}$ |
onde, d é o comprimento do diâmetro.
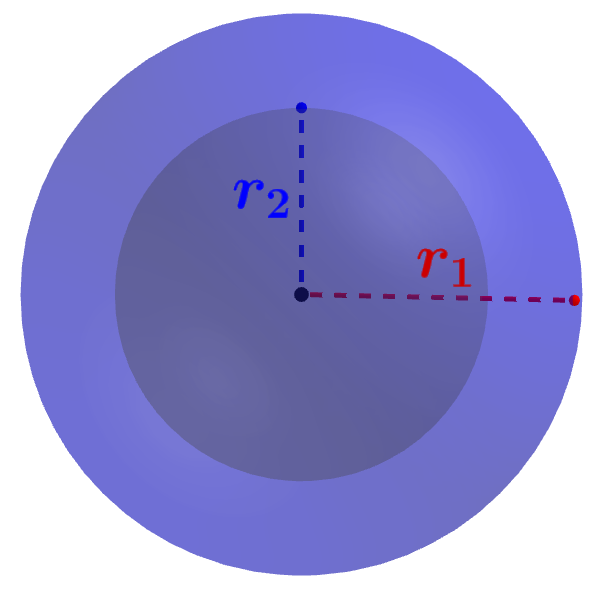
Calcular o volume de uma esfera oca
Podemos calcular o volume de uma esfera oca subtraindo o volume da parte oca do volume total da esfera. Então, se usarmos $latex r_{1}$ para representar o raio da esfera inteira e $latex r_{2}$ para representar o raio interno, ou seja, o raio da parte oca, temos:
$latex V=\frac{4}{3}\pi {{r_{1}}^3}-\frac{4}{3}\pi {{r_{2}}^3}$
Simplificando, podemos obter a seguinte fórmula:
| $latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$ |
Área e volume de uma esfera – Exercícios resolvidos
As fórmulas para a área e o volume de uma esfera são usadas para resolver os seguintes exercícios. Tente resolver os exercícios antes de olhar para a solução.
EXERCÍCIO 1
Encontre a área de uma esfera com um raio de 4 mm.
Solução
Usando a fórmula da área com comprimento $latex r=4$, temos:
$latex A_{s}=4\pi {{r}^2}$
$latex A_{s}=4\pi {{(4)}^2}$
$latex A_{s}=4\pi (16)$
$latex A_{s}=201,1$
A área da esfera é igual a 201,1 mm².
EXERCÍCIO 2
Encontre o volume de uma esfera com um raio de 3 cm.
Solução
Usando a fórmula para volume em termos de raio com $latex r=3$, temos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(3)}^3}$
$latex V=\frac{4}{3}\pi (27)$
$latex V=113,1$
O volume é igual a 113,1 cm³.
EXERCÍCIO 3
Qual é a área de uma esfera com um raio de 5 cm?
Solução
Usamos o raio $latex r=5$ na fórmula da área. Então temos:
$latex A_{s}=4\pi {{r}^2}$
$latex A_{s}=4\pi {{(5)}^2}$
$latex A_{s}=4\pi (25)$
$latex A_{s}=314,2$
A área da esfera é igual a 314,2 cm².
EXERCÍCIO 4
Qual é o volume de uma esfera com um raio de 4 mm?
Solução
Usando a fórmula para volume em termos de raio com comprimento $latex r=4$, temos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(4)}^3}$
$latex V=\frac{4}{3}\pi (64)$
$latex V=268,1$
O volume é igual a 268,1 mm³.
EXERCÍCIO 5
Encontre a área de uma esfera com um diâmetro de 12 cm.
Solução
Como temos o comprimento do diâmetro, podemos dividi-lo por 2 para obter o raio. Então, usamos a fórmula da área da esfera com comprimento $latex r=6$:
$latex A_{s}=4\pi {{r}^2}$
$latex A_{s}=4\pi {{(6)}^2}$
$latex A_{s}=4\pi (36)$
$latex A_{s}=452,4$
A área da esfera é igual a 452,4 cm².
EXERCÍCIO 6
Encontre o volume de uma esfera com um diâmetro de 5 m.
Solução
Como temos o diâmetro da esfera, podemos dividi-lo por 2 para obter o raio. Isso significa que o raio é igual a $latex r=2,5$. Então temos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(2,5)}^3}$
$latex V=\frac{4}{3}\pi (6,25)$
$latex V=26,2$
O volume é igual a 26,2 m³.
EXERCÍCIO 7
Qual é o raio de uma esfera com uma área de 200 cm²?
Solução
Neste caso, conhecemos a área e queremos encontrar o comprimento do raio. Então, vamos usar a fórmula da área da esfera e resolver para r:
$latex A_{s}=4\pi {{r}^2}$
$latex 200=4\pi {{r}^2}$
$latex 50=\pi {{r}^2}$
$latex 15.92={{r}^2}$
$latex r=3,99$
O comprimento do raio é 3,99 cm.
EXERCÍCIO 8
Encontre o volume de uma esfera oca que tem um raio externo de 6 cm e um raio interno de 4 cm.
Solução
A esfera oca tem raios $latex r_{1}=6$ e $latex r_{2}=4$. Assim, podemos usar a fórmula para o volume de uma esfera oca com estes raios:
$latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$
$latex V=\frac{4}{3}\pi ({{(6)}^3}-{{(4)}^3})$
$latex V=\frac{4}{3}\pi (216-64)$
$latex V=\frac{4}{3}\pi (152)$
$latex V=636,7$
O volume é igual a 636,7 cm³.
EXERCÍCIO 9
Encontre o raio de uma esfera com uma área de 460 m².
Solução
Vamos usar a fórmula da área da esfera e resolver para r:
$latex A_{s}=4\pi {{r}^2}$
$latex 460=4\pi {{r}^2}$
$latex 115=\pi {{r}^2}$
$latex 36,6={{r}^2}$
$latex r=6,05$
O comprimento do raio é de 6,05 m.
EXERCÍCIO 10
Qual é o volume de uma esfera oca que tem um raio externo de 5 mm e um raio interno de 4 mm?
Solução
Os raios da esfera oca são $latex r_{1}=5$ e $latex r_{2}=4$. Então temos:
$latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$
$latex V=\frac{4}{3}\pi ({{(5)}^3}-{{(4)}^3})$
$latex V=\frac{4}{3}\pi (125-64)$
$latex V=\frac{4}{3}\pi (152)$
$latex V=255,5$
O volume é igual a 255,5 mm³.
Área e volume de uma esfera – Exercícios para resolver
Use as fórmulas para a área e o volume de uma esfera para resolver os exercícios a seguir. Clique em “Verificar” para verificar se sua resposta está correta.
Veja também
Interessado em aprender mais sobre área e volume de figuras geométricas? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
