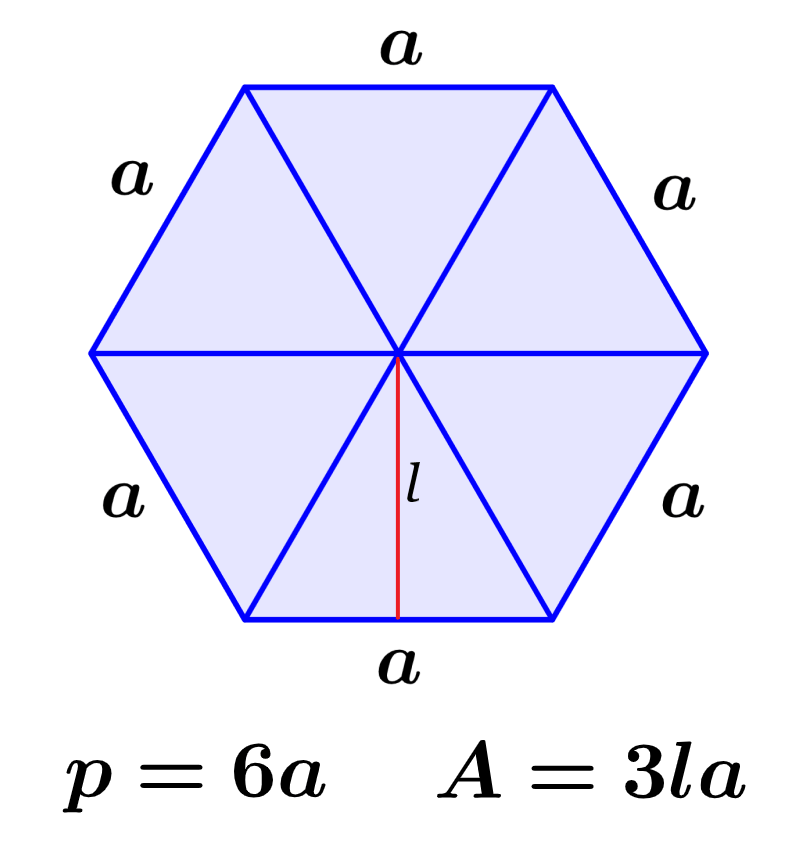
O perímetro de um hexágono é o comprimento total de seu contorno. Por outro lado, a área representa o espaço bidimensional ocupado pela figura. Podemos encontrar o perímetro de um hexágono somando os comprimentos de seus seis lados, e podemos encontrar sua área multiplicando três por seu apótema e pelo comprimento de um de seus lados.
A seguir, aprenderemos tudo sobre o perímetro e a área dos hexágonos. Conheceremos suas fórmulas e as aplicaremos para resolver alguns exercícios práticos.
Como calcular o perímetro de um hexágono?
Podemos calcular o perímetro de um hexágono somando os comprimentos de seus seis lados. Assim, podemos usar a seguinte fórmula:
$latex p=a+b+c+d+e+f$
onde, $latex a.~b,~c,~d,~e,~f$ são os seis comprimentos dos lados do hexágono.
Se tivermos um hexágono regular, sabemos que todos os seis lados têm o mesmo comprimento, então a fórmula do perímetro é:
| $latex p=6a$ |
onde, a é o comprimento de um dos lados do hexágono regular.
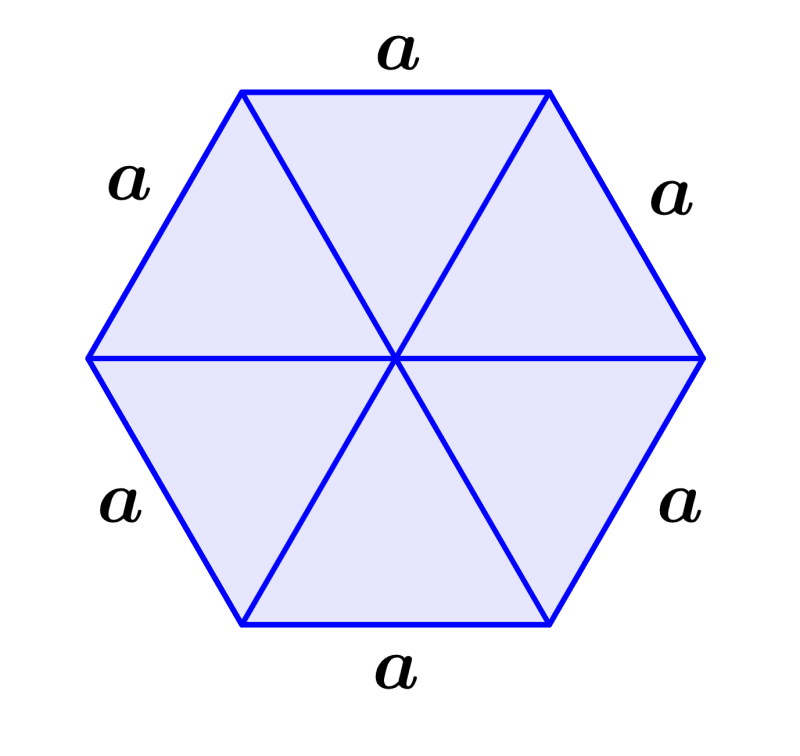
Como calcular a área de um hexágono?
Podemos calcular a área de um hexágono regular usando o comprimento de um de seus lados e o comprimento de seu apótema. Assim, podemos usar a seguinte fórmula:
| $latex A=3la$ |
onde, l é o comprimento de um dos lados do hexágono e a é o comprimento do apótema. Lembre-se que o apótema é o segmento que liga o centro do hexágono com um de seus lados.
Prova da fórmula para a área de um hexágono
Podemos demonstrar a fórmula da área de um hexágono usando o diagrama a seguir, onde dividimos o hexágono em seis triângulos congruentes.
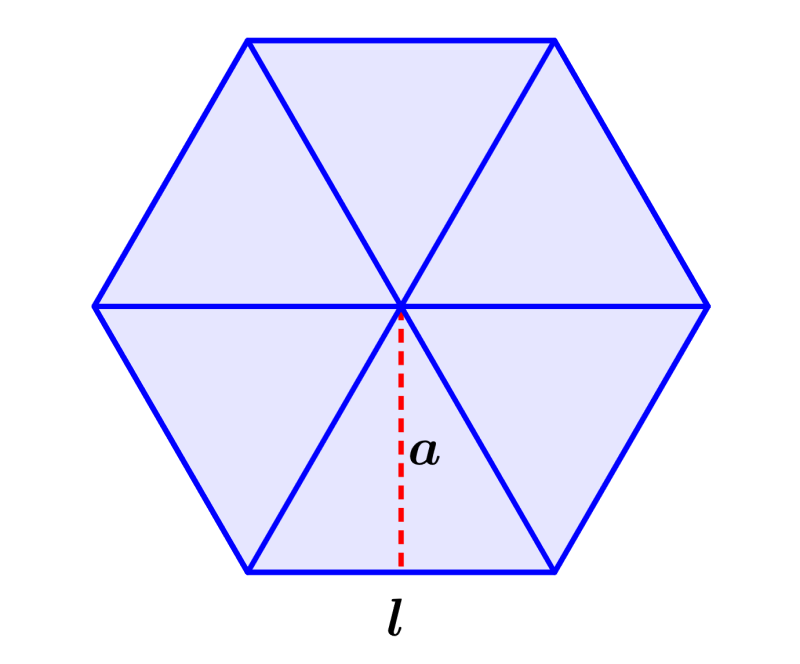
Agora, sabemos que a área de qualquer triângulo pode ser calculada usando a fórmula $latex A=\frac{1}{2}bh$, onde b é o comprimento da base e h é o comprimento da altura.
Neste diagrama, a base de cada triângulo é igual a um lado do hexágono e a altura é igual ao apótema, então a área de cada triângulo é igual a $latex A=\frac{1}{2}la $ .
Por fim, vemos que temos 6 triângulos equiláteros no hexágono, então multiplicamos a área obtida por 6 para obter $latex A=3la$, que é a área do hexágono.
Calcular a área do hexágono sem usar o apótema
Podemos obter uma fórmula para encontrar a área de um hexágono sem usar o comprimento do apótema. Para conseguir isso, precisamos encontrar uma expressão para o comprimento do apótema em termos do comprimento de um dos lados do hexágono.
Observando que os triângulos que traçamos no hexágono são equiláteros, podemos usar a fórmula da Altura de um Triângulo Equilátero: $latex h=\frac{\sqrt{3}}{2}l$, onde l é o comprimento de um dos lados do hexágono.
Então, substituindo este valor pelo valor de a, temos:
| $latex A=3l(\frac{\sqrt{3}}{2}l)$ $latex A=\frac{3\sqrt{3}}{2}{{l}^2}$ |
Área e perímetro de um hexágono – Exercícios resolvidos
EXERCÍCIO 1
Encontre o perímetro de um hexágono regular com lados de 5 mm.
Solução
Usando a fórmula do perímetro com comprimento $latex a=5$, temos:
$latex p=6a$
$latex p=6(5)$
$latex p=30$
O perímetro do hexágono é igual a 30 mm.
EXERCÍCIO 2
Encontre a área de um hexágono regular com lados de 4 cm de comprimento e um apótema de 3,46 cm de comprimento.
Solução
Temos os seguintes comprimentos:
- Lados, $latex l=4$ cm
- Apotema, $latex a=3,46$ cm
Podemos usar a fórmula da área com os comprimentos dados:
$latex A=3la$
$latex A=3(4)(3,46)$
$latex A=41,52$
A área do hexágono é igual a 41,52 cm².
EXERCÍCIO 3
Encontre o perímetro de um hexágono regular com lados de 6 cm de comprimento.
Solução
Usamos o comprimento $latex a=6$ na fórmula do perímetro. Então temos:
$latex p=6a$
$latex p=6(6)$
$latex p=36$
O perímetro do hexágono é igual a 36 cm.
EXERCÍCIO 4
Qual é a área de um hexágono regular com lados de 6 cm de comprimento e apótema de 5,2 cm de comprimento?
Solução
Temos as seguintes informações:
- Lados, $latex l=6$ cm
- Apothem, $latex a=5,2$ cm
Usando a fórmula da área com esses comprimentos, temos:
$latex A=3la$
$latex A=3(6)(5,2)$
$latex A=93,6$
A área do hexágono é igual a 93,6 cm².
EXERCÍCIO 5
Qual é o perímetro de um hexágono regular com lados de 13 cm de comprimento?
Solução
Usando a fórmula do perímetro com $latex a=13$, temos:
$latex p=6a$
$latex p=6(13)$
$latex p=78$
O perímetro do hexágono é igual a 78 cm.
EXERCÍCIO 6
Encontre a área de um hexágono regular com lados de 7 m de comprimento e um apótema de 6,06 m.
Solução
Temos o seguinte:
- Lados, $latex l=7$ m
- Apothem, $latex a=6,06$ m
Usando isso na fórmula da área, temos:
$latex A=3la$
$latex A=3(7)(6,06)$
$latex A=127,26$
A área do hexágono é igual a 127,26 m².
EXERCÍCIO 7
Qual é o comprimento dos lados de um hexágono regular com um perímetro de 72 m?
Solução
Aqui, conhecemos o perímetro e vamos encontrar o comprimento dos lados do hexágono. Então, usamos a fórmula do perímetro com $latex p=72$ e resolvemos para a:
$latex p=6a$
$latex 72=6a$
$latex a=12$
O comprimento dos lados é de 12 m.
EXERCÍCIO 8
Encontre a área de um hexágono regular com lados de comprimento 5 mm.
Solução
Neste caso, sabemos apenas o comprimento de um lado do hexágono, então podemos usar a fórmula da segunda área com comprimento $latex l=5$:
$latex A=\frac{3\sqrt{3}}{2}{{l}^2}$
$latex A=\frac{3\sqrt{3}}{2}{{(5)}^2}$
$latex A=\frac{3\sqrt{3}}{2}(25)$
$latex A=64,96$
A área do hexágono é igual a 64,96 mm².
EXERCÍCIO 9
Encontre o comprimento dos lados de um hexágono regular com um perímetro de 126 cm.
Solução
Podemos encontrar o comprimento dos lados do hexágono usando a fórmula do perímetro com $latex p=126$ e resolver para a:
$latex p=6a$
$latex 126=6a$
$latex a=21$
O comprimento dos lados é de 21 cm.
EXERCÍCIO 10
Qual é a área de um pentágono com lados de 8 m de comprimento?
Solução
Usamos a segunda fórmula de área, pois só temos o comprimento de um lado do hexágono. Então, usamos o comprimento $latex l=6$ na fórmula:
$latex A=\frac{3\sqrt{3}}{2}{{l}^2}$
$latex A=\frac{3\sqrt{3}}{2}{{(8)}^2}$
$latex A=\frac{3\sqrt{3}}{2}(64)$
$latex A=166,28$
A área do hexágono é igual a 166,28 m².
Área e perímetro de um hexágono – Exercícios para resolver
Veja também
Interessado em aprender mais sobre perímetros e áreas de figuras geométricas? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
