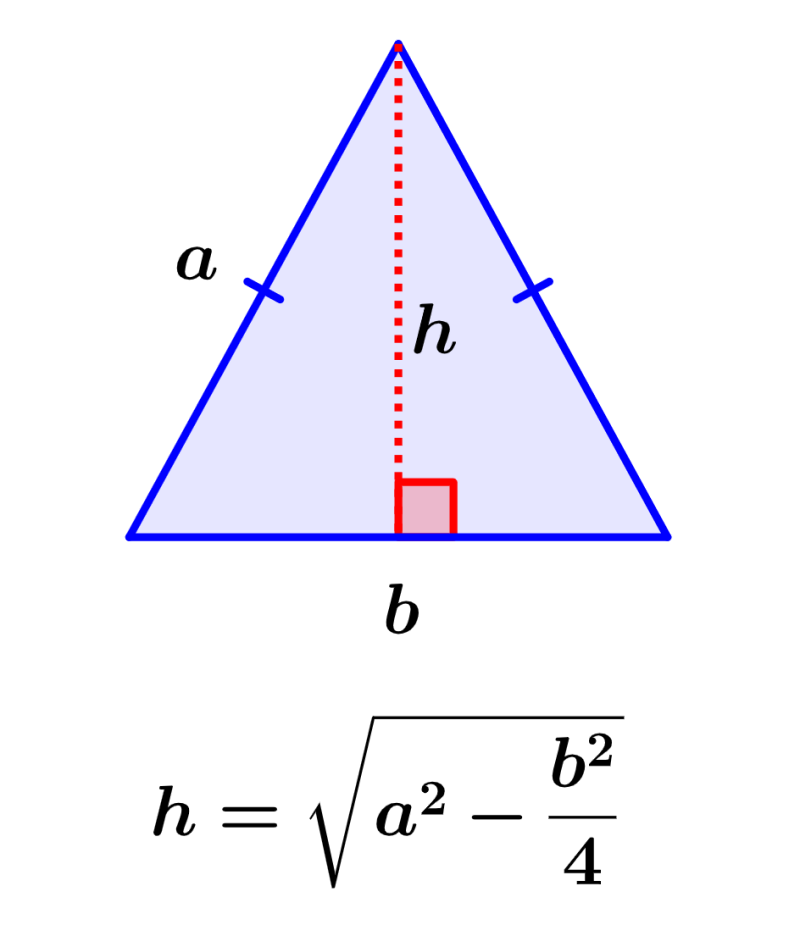
A altura de um triângulo isósceles é a distância perpendicular da base ao vértice oposto. Para calcular a altura, podemos usar o teorema de Pitágoras e derivar uma fórmula que depende do comprimento da base e do comprimento de um dos lados congruentes.
A seguir, aprenderemos como derivar a fórmula para a altura dos triângulos isósceles. Além disso, usaremos esta fórmula para resolver alguns exercícios práticos.
Fórmula para a altura de um triângulo isósceles
A altura de um triângulo isósceles é calculada usando o comprimento de sua base e o comprimento de um dos lados congruentes. Podemos calcular a altura usando a seguinte fórmula:
| $latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$ |
onde, a é o comprimento dos lados congruentes do triângulo e b é o comprimento da base do triângulo.
Derivação da fórmula de altura
Para derivar essa fórmula, podemos considerar o seguinte triângulo isósceles:
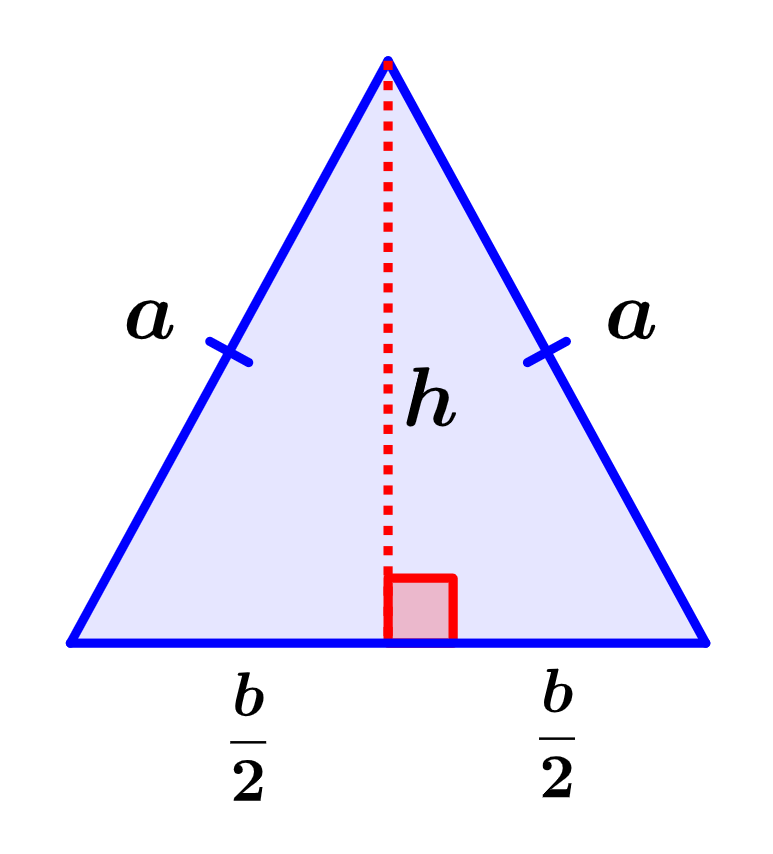
Desenhando uma linha que representa a altura, podemos ver que dividimos o triângulo isósceles em dois triângulos retângulos congruentes. Podemos usar um dos triângulos obtidos e aplicar o teorema de Pitágoras para calcular a altura.
Lembre-se de que o teorema de Pitágoras nos diz que o quadrado da hipotenusa é igual à soma dos quadrados dos lados. Então, temos:
$latex {{a}^2}={{h}^2}+{{( \frac{b}{2})}^2}$
$latex {{a}^2}={{h}^2}+ \frac{{{b}^2}}{4}$
$latex {{h}^2}={{a}^2}- \frac{{{b}^2}}{4}$
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
Obtivemos uma expressão para a altura.
Exercícios de altura de triângulos isósceles resolvidos
Os exercícios a seguir usam a fórmula vista para encontrar a altura dos triângulos isósceles. Tente resolver os exercícios sozinho antes de olhar para a solução.
EXERCÍCIO 1
Qual é a altura de um triângulo isósceles que tem uma base de 8 m e lados congruentes de 6 m de comprimento?
Solução
Da pergunta, temos os seguintes dados:
- Base, $latex b=8$ m
- Lados, $latex a=6$ m
Portanto, usamos a fórmula de altura com estes valores:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{6}^2}- \frac{{{8}^2}}{4}}$
$latex h= \sqrt{36- \frac{64}{4}}$
$latex h= \sqrt{36-16}$
$latex h= \sqrt{20}$
$latex h=4,47$
A altura do triângulo é 4,47 m.
EXERCÍCIO 2
Um triângulo isósceles tem uma base de 10 m e lados congruentes de 12 m de comprimento. Qual é o comprimento da sua altura?
Solução
Podemos identificar as seguintes informações:
- Base, $latex b=10$ m
- Lados, $latex a=12$ m
Substituindo esses valores na fórmula, temos:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{12}^2}- \frac{{{10}^2}}{4}}$
$latex h= \sqrt{144- \frac{100}{4}}$
$latex h= \sqrt{144-25}$
$latex h= \sqrt{119}$
$latex h=10,91$
A altura do triângulo é de 10,91 m.
EXERCÍCIO 3
Um triângulo isósceles tem uma base de comprimento de 8 m e lados congruentes de comprimento de 9 m. Qual é o comprimento da altura?
Solução
Da pergunta, temos os seguintes valores:
- Base, $latex b=8$ m
- Lados, $latex a=9$ m
Substituindo esses valores na fórmula de altura, temos:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{9}^2}- \frac{{{8}^2}}{4}}$
$latex h= \sqrt{81- \frac{64}{4}}$
$latex h= \sqrt{81-16}$
$latex h= \sqrt{65}$
$latex h=8,06$
A altura do triângulo é de 8,06 m.
EXERCÍCIO 4
Qual é a altura de um triângulo que tem uma base de comprimento de 14 m e lados congruentes de comprimento de 11 m?
Solução
Temos as seguintes informações:
- Base, $latex b=14$ m
- Lados, $latex a=11$ m
Portanto, usamos a fórmula de altura com estes valores:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{11}^2}- \frac{{{14}^2}}{4}}$
$latex h= \sqrt{121- \frac{196}{4}}$
$latex h= \sqrt{121-49}$
$latex h= \sqrt{72}$
$latex h=8,49$
A altura do triângulo é de 8,49 m.
Exercícios de altura de triângulos isósceles para resolver
Use a fórmula para a altura dos triângulos isósceles para resolver os seguintes problemas. Se precisar de ajuda, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre triângulos isósceles? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
