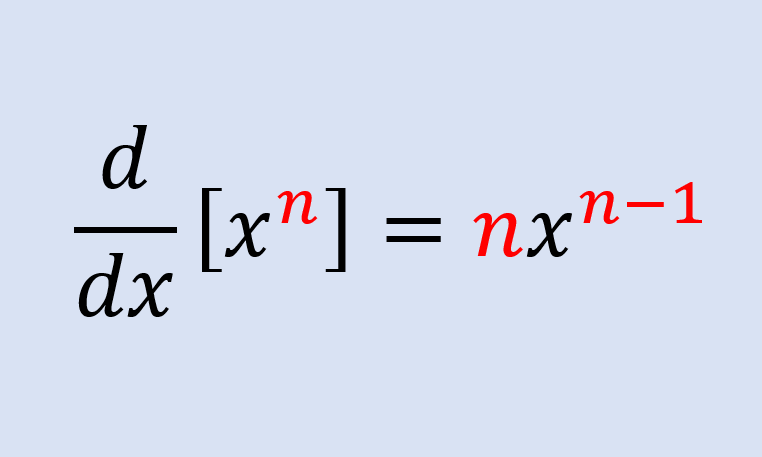A regra da potência é uma das fórmulas mais utilizadas no Cálculo Diferencial. Esta regra é aplicada para resolver derivadas de funções com um único termo. A regra da potência nos permite calcular facilmente as derivadas, pois não precisamos usar a fórmula para uma derivada com limites.
A seguir, aprenderemos como encontrar derivadas de funções com apenas um termo. Vamos conhecer a fórmula e aplicá-la para resolver alguns exercícios.
- A regra da potência e sua fórmula
- Casos especiais e formas da fórmula da regra de potência
- Provas da regra da potência
- Quando usar a fórmula da regra da potência
- Como usar a regra da potência para encontrar derivadas, um tutorial passo a passo
- Regra da potência – Exemplos com respostas
- Regra da Potência – Problemas de Prática
- Veja também
- Definição e fórmula da regra da potência
- Passos para usar a regra da potência das derivadas
- Exemplos da regra da potência das derivadas
- Regra da potência das derivadas – Exercícios para resolver
- Veja também
Definição e fórmula da regra da potência
A regra da potência das derivadas nos diz que a derivada de uma variável elevada a um expoente numérico é igual ao valor do expoente numérico multiplicado pela variável elevada ao valor do expoente numérico subtraído por um.
A regra da potência permite obter derivadas de funções com expoentes numéricos sem a necessidade de usar a fórmula para uma derivada com limites.
Outras formas e casos da regra da potência também existem, como o caso dos polinômios, mas serão revistos quando aprendermos as regras de derivadas aplicáveis.
Fórmula da regra básica da potência
A fórmula da regra da potência é:
| $$\frac{d}{dx}(x^n) = nx^{n-1}$$ |
Onde
- $latex n =$ o valor numérico do expoente limitado apenas a números reais
- $latex x =$ a variável que é elevada a um expoente numérico $latex n$
Também podemos denotar $latex \frac{d}{dx}(x^n)$ com $latex y’$, $latex F'(x)$, $latex f'(x)$, ou outras letras usadas para denotam funções com o símbolo do apóstrofo.
Passos para usar a regra da potência das derivadas
Suponha que temos que derivar
$latex f(x) = x^2$
Temos uma função com uma variável elevada a uma potência de 2. Para derivar esse problema, vamos usar a regra da potência conforme mostrado nos passos a seguir:
Passo 1: Começamos escrevendo a fórmula para a regra da potência:
$latex f'(x^n) = nx^{n-1}$
Passo 2: Se a função contiver radicais ou expressões racionais, usamos as leis dos expoentes para converter para a forma exponencial. Neste caso, não temos radicais ou expressões racionais.
Nota: Um exemplo seria escrever $latex \sqrt{x}$ como $latex x^{\frac{1}{2}}$.
Passo 3: Determine o expoente da variável. Nesse caso, nosso expoente é 2. Portanto,
$latex n = 2$
Passo 4: Aplique a fórmula da regra da potência para derivar o problema:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (x^2)$$
$$\frac{d}{dx} (x^2) = 2 \cdot x^{2-1}$$
Passo 5: Simplifique a expressão resultante:
$$\frac{d}{dx} (x^2) = 2x^{1}$$
$$f'(x) = 2x$$
Você pode usar $latex f'(x), y’,$ ou $latex \frac{d}{dx}(f(x))$ como o símbolo de derivada no lado esquerdo da resposta final em vez de $latex ( x^n)’$ ou $latex \frac{d}{dx}(x^n)$.
Exemplos da regra da potência das derivadas
Cada um dos exemplos a seguir tem sua respectiva solução detalhada, onde aplicamos a regra da potência.
EXEMPLO 1
Encontre a derivada de $latex f(x)=x^3$.
Solução
Passo 1: Começamos com a fórmula:
$latex f'(x^n) = nx^{n-1}$
Passo 2: A expressão tem um expoente numérico, então não precisamos fazer este passo.
Passo 3: Neste caso, o expoente é 3. Então,
$latex n = 3$
Passo 4: Usando a regra da potência, temos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (x^3)$$
$$\frac{d}{dx} (x^3) = 3 \cdot x^{3-1}$$
Passo 5: Simplificando, temos:
$$\frac{d}{dx} (x^3) = 3 x^2$$
$$f'(x)= 3 x^2$$
EXEMPLO 2
Encontre a derivada da função $latex f(x)=5x^4$.
Solução
Passo 1: Temos a fórmula:
$latex f'(x^n) = nx^{n-1}$
Passo 2: O expoente da variável é um inteiro, então não precisamos reescrevê-lo.
Passo3: Neste caso, o expoente é 4. Então,
$latex n = 4$
Passo 4: Aplicando a regra da potência, temos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (5x^4)$$
$$\frac{d}{dx} (5x^4) = 4 \cdot (5x^{4-1})$$
Passo 5: Simplificando, temos:
$$\frac{d}{dx} (5x^4) = 20 x^3$$
$$f'(x)= 20 x^3$$
EXEMPLO 3
Determine a derivada da função $latex f(x)=10x^7$.
Solução
Passo 1: A fórmula para a regra da potência das derivadas é:
$latex f'(x^n) = nx^{n-1}$
Passo 2: A expressão tem um expoente numérico, então não precisamos fazer este passo.
Passo 3: O expoente da expressão é 7. Então, temos:
$latex n = 7$
Passo 4: Quando aplicamos a regra da potência, temos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (10x^7)$$
$$\frac{d}{dx} (10x^7) = 7 \cdot (10x^{7-1})$$
Passo 5: Simplificando, temos:
$$\frac{d}{dx} (10x^7) = 70 x^6$$
$$f'(x)= 70 x^6$$
EXEMPLO 4
Derive a função: $latex f(x) = -12x^{-13}$.
Solução
Passo 1: Temos a fórmula:
$latex f'(x^n) = nx^{n-1}$
Passo 2: A expressão é dada na forma exponencial.
Passo 3: Determine o expoente da variável. Nesse caso, nosso expoente é -13. Então,
$latex n = -13$
Passo 4: Derivamos usando a regra da potência:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (-12x^{-13})$$
$$\frac{d}{dx} (-12x^{-13}) = -13 \cdot (-12 x^{-13-1})$$
Passo 5: Simplificando, temos:
$$\frac{d}{dx} (-12x^{-13}) = 156x^{-14}$$
Como o expoente é negativo, podemos aplicar as leis dos expoentes para simplificá-lo ainda mais racionalmente, embora isso seja opcional:
$$\frac{d}{dx} (x^n) = \frac{156}{x^{14}}$$
A resposta final é:
$$f'(x) = \frac{156}{x^{14}}$$
EXEMPLO 5
Encontre a derivada de $latex f(x)=\sqrt{x}$.
Solução
Passo 1: Começamos com a fórmula da regra da potência:
$latex f'(x^n) = nx^{n-1}$
Passo 2: Temos que usar a lei dos expoentes radicais para reescrever a expressão:
$$ \sqrt{x}=x^{\frac{1}{2}}$$
Passo 3: Agora, vemos que o expoente é 1/2. Então,
$latex n = \frac{1}{2}$
Passo 4: Usando a regra da potência na função, temos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (x^{\frac{1}{2}})$$
$$\frac{d}{dx} (x^{\frac{1}{2}}) = \frac{1}{2} \cdot ( x^{\frac{1}{2}-1})$$
Passo 5: Simplificando, temos:
$$f'(x) = \frac{1}{2} x^{-\frac{1}{2}}$$
Simplificando, temos: Podemos assim usar dois expoentes para expressar da seguinte forma:
$$f'(x) = \frac{1}{2x^{\frac{1}{2}}}$$
$$f'(x) = \frac{1}{2\sqrt{x}}$$
EXEMPLO 6
Encontre a derivada de $latex f(x)=\frac{1}{\sqrt{x}}$.
Solução
Passo 1: A fórmula da regra da potência é:
$latex f'(x^n) = nx^{n-1}$
Passo 2: Usando as regras dos expoentes, podemos escrever da seguinte forma:
$$ \frac{1}{\sqrt{x}}=x^{-\frac{1}{2}}$$
Passo 3: O expoente da expressão é -1/2. Então temos:
$latex n = -\frac{1}{2}$
Passo 4: Aplicando a regra da potência na função, temos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (x^{-\frac{1}{2}})$$
$$\frac{d}{dx} (x^{-\frac{1}{2}}) = -\frac{1}{2} \cdot ( x^{-\frac{1}{2}-1})$$
Passo 5: Simplificando, temos:
$$f'(x) = -\frac{1}{2} x^{-\frac{3}{2}}$$
Usamos as leis dos expoentes para escrever da seguinte forma:
$$f'(x) = -\frac{1}{2x^{\frac{3}{2}}}$$
$$f'(x) = -\frac{1}{2\sqrt{x^3}}$$
Regra da potência das derivadas – Exercícios para resolver
Use a regra da potência para encontrar as derivadas das seguintes funções.
Veja também
Interessado em aprender mais sobre derivadas de funções? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
