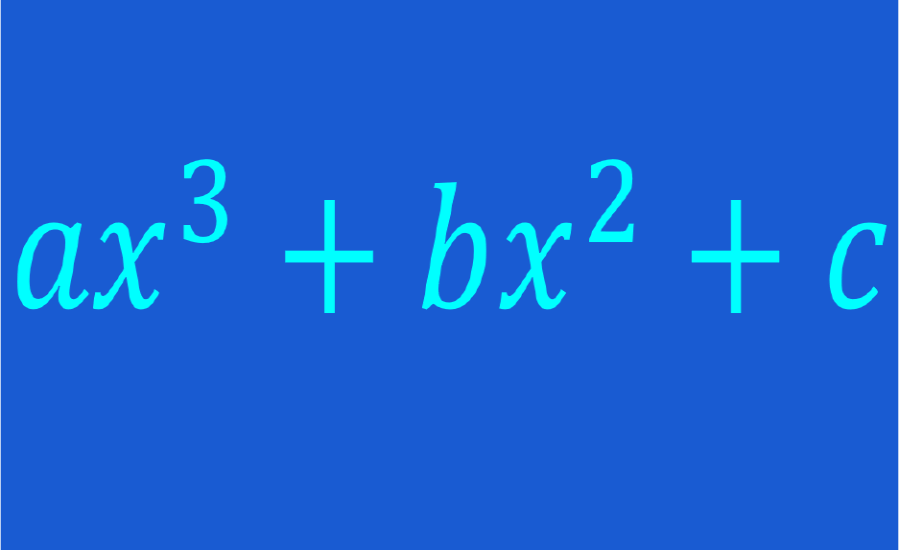A multiplicidade de raízes se refere ao número de vezes que cada raiz aparece em um determinado polinômio. Determinar a multiplicidade das raízes dos polinômios é fácil se tivermos a versão fatorada do polinômio. Alternativamente, também é possível determinar a multiplicidade das raízes observando o gráfico do polinômio.
A seguir, aprenderemos sobre a multiplicidade de raízes e como determinar a multiplicidade de raízes algebricamente. Além disso, também aprenderemos a encontrar a multiplicidade de raízes usando os gráficos de polinômios.
Zeros e multiplicidade de raízes
As raízes reais de um polinômio correspondem aos interceptos x do gráfico do polinômio. Portanto, podemos encontrar informações sobre o número de raízes reais de um polinômio observando seu gráfico. Da mesma forma, podemos determinar quantas vezes o gráfico irá tocar ou cruzar o eixo x olhando para os zeros do polinômio ou a forma fatorada do polinômio.
Um zero ou uma raiz tem uma multiplicidade, que se refere ao número de vezes que seu fator associado aparece no polinômio. Por exemplo, o quadrático $latex (x+2)(x-3)$ tem as raízes $latex x= -2$ e $latex x=3$, cada uma ocorrendo apenas uma vez.
O polinômio de quinto grau $latex {{(x+2)}^3}{{(x-3)}^2}$ tem as mesmas raízes que o quadrático, mas, neste caso, a raiz $latex x=-2$ tem uma multiplicidade de 3 já que o fator $latex (x+2)$ aparece três vezes (é ao cubo).
Da mesma forma, a raiz $latex x=3$ tem uma multiplicidade de 2, pois o fator $latex (x-3)$ aparece duas vezes (é ao quadrado).
Se tivermos um polinômio em sua forma fatorada, podemos facilmente determinar a multiplicidade das raízes. Simplesmente temos que contar o número de vezes que cada raiz aparece no polinômio.
Se o polinômio não estiver em sua forma fatorada, precisamos fatorá-lo, se possível, ou obter um gráfico do polinômio para observar seu comportamento ao cruzar ou chocar com o eixo x.
EXEMPLO
- Encontre a multiplicidade das raízes do polinômio $latex {{(x+5)}^2}{{(x-2)}^4}{{(x-3)}^3}$.
Solução: As raízes do polinômio são $latex x=-5$, $latex x=2$ e $latex x = 3$. Para encontrar sua multiplicidade, basta contar quantas vezes cada raiz aparece. Nesse caso, a multiplicidade é o expoente ao qual cada fator é elevado.
- A raiz $latex x=-5$ tem uma multiplicidade de 2.
- A raiz $latex x=2$ tem uma multiplicidade de 4.
- A raiz $latex x=3$ tem uma multiplicidade de 3.
Multiplicidade de raízes de gráficos de polinômios
Os gráficos de polinômios se comportam de maneira diferente em vários interceptos x. Às vezes, o gráfico cruza completamente o eixo x em uma interceptação. Outras vezes, o gráfico tocará o eixo x e salta.
Suponha que temos o gráfico da função polinomial $latex f(x)=(x+4){{(x-2)}^2}{{(x + 2)}^3}$. Observe que o comportamento em cada uma das raízes é diferente:
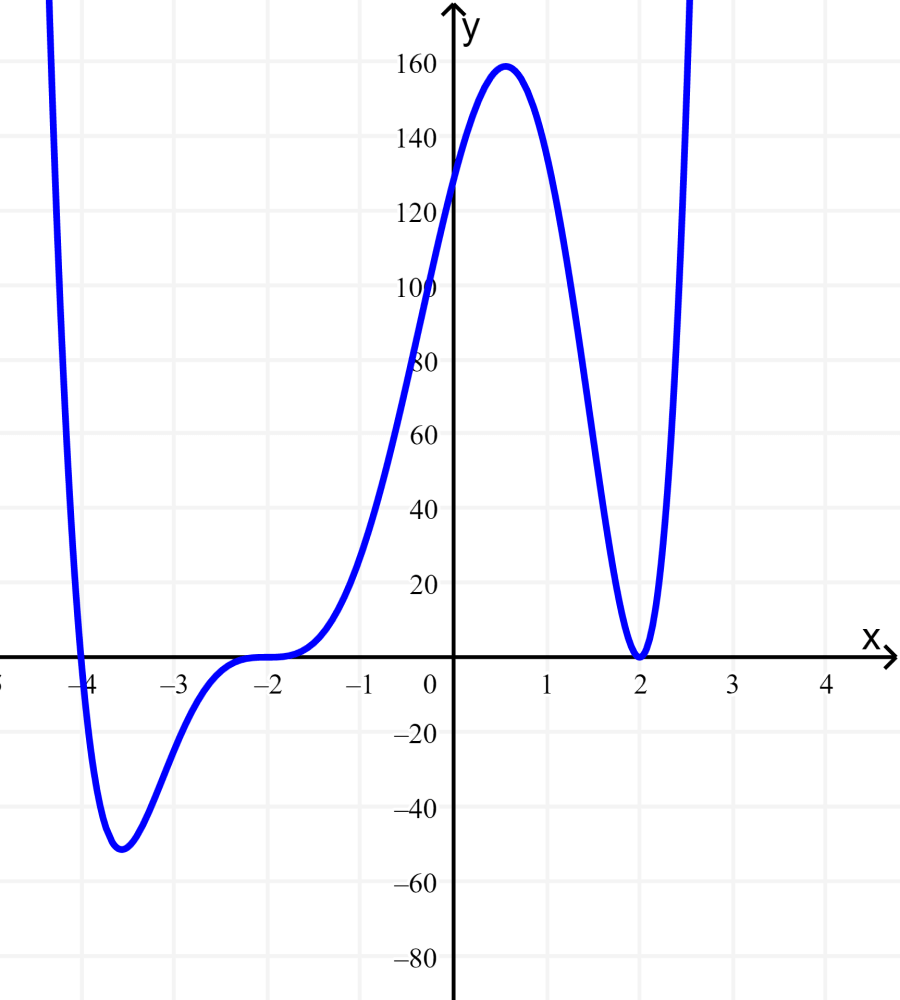
A interceptação em $latex x=-4$ é a solução para a equação $latex x+4= 0$. O gráfico passa diretamente pela interceptação em $latex x=-4$. O fator é linear, então o comportamento próximo à interceptação é semelhante a uma linha. Esta é uma raiz única, pois a raiz corresponde a um único fator.
A interceptação em $latex x=2$ é a solução repetida da equação $latex {{(x-2)}^2}=0$. O gráfico toca o eixo x na interceptação e muda de direção.
O fator é quadrático, então o comportamento próximo à interceptação é semelhante a um quadrático, ou seja, ele salta quando atinge o eixo x. O fator $latex (x-2)$ aparece duas vezes. Portanto, a raiz $latex x =2$ tem multiplicidade 2.
A interceptação em $latex x=-2$ é a solução repetida do fator $latex {{(x+2)}^3}=0$. O gráfico passa pelo eixo x na interceptação, mas fica um pouco plano à medida que o cruza. Este fator é cúbico, então o comportamento próximo ao intercepto é cúbico, ou seja, tem uma forma de S semelhante à função $latex f(x)={{x}^3}$. Essa raiz possui uma multiplicidade de 3.
Para raízes com multiplicidades pares, os gráficos se tocam ou são tangentes ao eixo x nesses valores de x. Para raízes com multiplicidades ímpares, os gráficos cruzam o eixo x nesses valores x. Os gráficos a seguir ilustram o comportamento de polinômios com multiplicidade 1, 2 e 3.
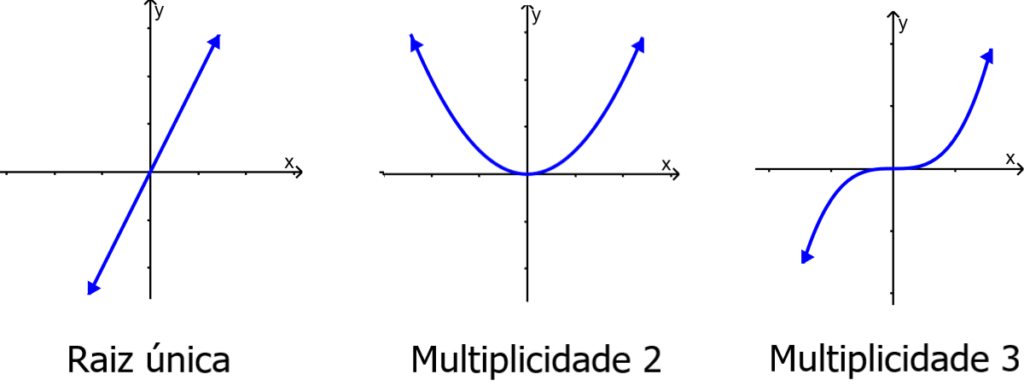
Para potências pares maiores, como 4, 6, 8, o gráfico continuará tocando o eixo x e saltando, mas com cada aumento na potência, o gráfico parecerá achatar mais e mais à medida que se aproxima e se afasta de x– eixo.
Da mesma forma, para potências ímpares maiores, como 5, 7, 9, o gráfico continuará a cruzar o eixo x, mas conforme as potências aumentam, o gráfico parecerá ficar mais plano conforme você se move para mais perto e mais longe do eixo x.
Identifique raízes e suas multiplicidades usando gráficos polinomiais
Portanto, resumindo o que temos acima, podemos encontrar as multiplicidades das raízes dos polinômios tendo o seguinte em mente:
- Se o gráfico cruza o eixo x e parece ser linear próximo à interceptação, a raiz é única.
- Se o gráfico tocar o eixo x e salta, a raiz terá uma multiplicidade par.
- Se o gráfico cruzar o eixo x em uma raiz, a raiz terá uma multiplicidade ímpar.
- A soma das multiplicidades é o grau n do polinômio.
Vamos aplicar essas idéias no exemplo a seguir.
EXEMPLO
O gráfico abaixo representa um polinômio de grau 7. Use este gráfico para encontrar as raízes do polinômio e suas possíveis multiplicidades.
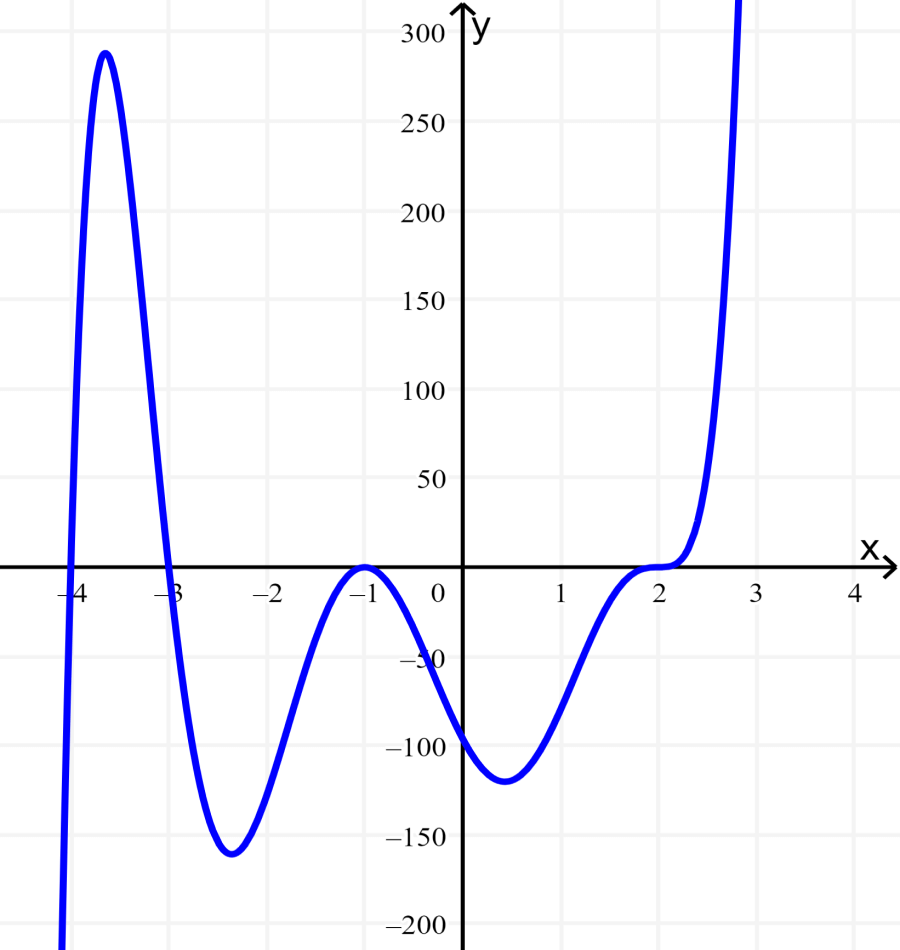
Solução: A função polinomial é de grau 7, então a soma das multiplicidades das raízes deve ser igual a 7.
Começando da esquerda, a primeira raiz ocorre em $latex x=-4$. O gráfico parece quase linear nesse ponto, então sabemos que essa raiz tem uma multiplicidade de 1.
Da mesma forma, vemos que a raiz que ocorre em $latex x=-3$ também parece linear, portanto, essa raiz também tem uma multiplicidade de 1.
Então temos uma raiz em $latex x=-1$. Vemos que, neste ponto, o gráfico toca o eixo x e salta, então sabemos que a raiz deve ter multiplicidade par. A raiz $latex x=-1$ tem multiplicidade 2.
O último zero ocorre em $latex x=2$. O gráfico cruza o eixo x, portanto, a multiplicidade dessa raiz deve ser ímpar. Sabemos que a multiplicidade dessa raiz deve ser 3 e a soma das multiplicidades é igual a 7.
Veja também
Você quer aprender mais sobre raízes complexas? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
