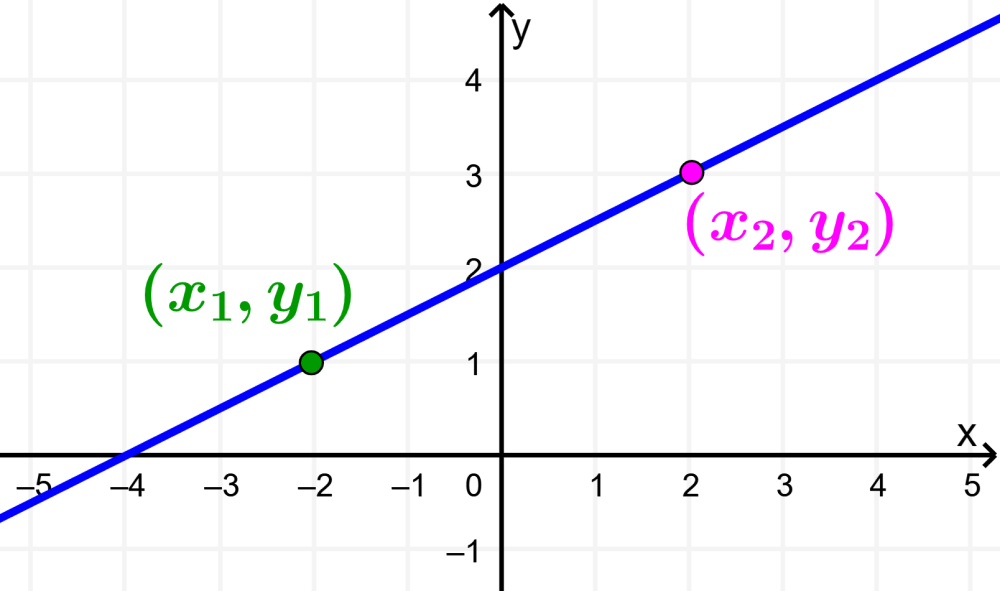
A equação da reta pode ser encontrada por vários métodos, dependendo das informações disponíveis. A forma dois pontos é um desses métodos. Esta forma é usada para encontrar a equação de uma reta que passa por dois pontos dados.
A seguir, veremos como encontrar a equação quando temos dois pontos e exploraremos vários exercícios para compreender totalmente o processo usado.
Resumo de equação da reta com dois pontos
Para encontrar a equação da reta que passa por dois pontos, lembramos que toda vez que queremos obter a equação de uma reta, precisamos de duas coisas: o declive e o intercepto y.
Portanto, se temos apenas dois pontos e nenhum declive, simplesmente usamos os dois pontos para encontrar o declive usando esta equação:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
Depois de obter o declive, usamos a forma declive intercepto $latex y=mx+b$ onde m é o declive e b é o intercepto y. A interceptação y pode ser encontrada usando um dos pontos fornecidos.
Alternativamente, podemos usar a forma de dois pontos de uma linha. Dados dois pontos $latex (x_{1}, ~ y_{1})$ e $latex (x_{2}, ~ y_{2})$, temos o seguinte:
| $latex y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$ ou $latex y-y_{2}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{2})$ |
Exercícios de equação da reta com dois pontos resolvidos
Os exercícios a seguir são resolvidos usando os dois métodos para encontrar a equação da reta usando os dois pontos indicados acima. A solução mostra o processo detalhado a seguir para obter a equação da reta.
EXERCÍCIO 1
Encontre a equação de uma reta que passa pelos pontos (3, 3) e (-1, 1).
Solução
O gráfico a seguir mostra a reta que passa pelos dois pontos:
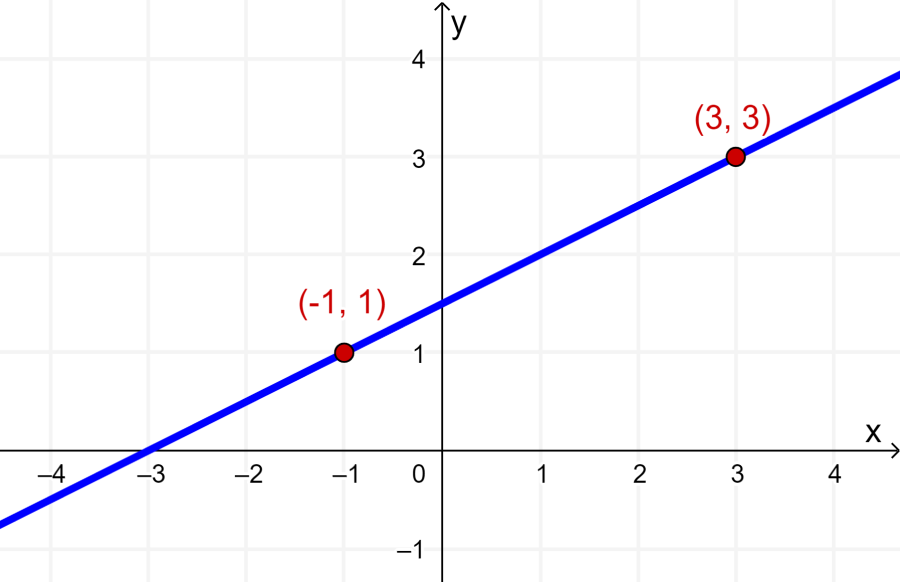
Os dois pontos são (-1, 1) e (3, 3). Então, podemos começar encontrando o declive da linha:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{3-1}{3-(-1)}$
$latex m=\frac{2}{4}=\frac{1}{2}$
Agora, usamos o ponto (-1, 1) para encontrar a interceptação em y:
$latex y=mx+b$
$latex 1= \frac{1}{2}(-1)+b$
$latex b= \frac{3}{2}$
Então, a equação da reta é:
$latex y=\frac{1}{2}x+\frac{3}{2}$
EXERCÍCIO 2
Encontre a equação da reta que passa pelos pontos (-2, -1) e (1, 2).
Solução
A seguir está o gráfico da reta que passa pelos pontos dados:
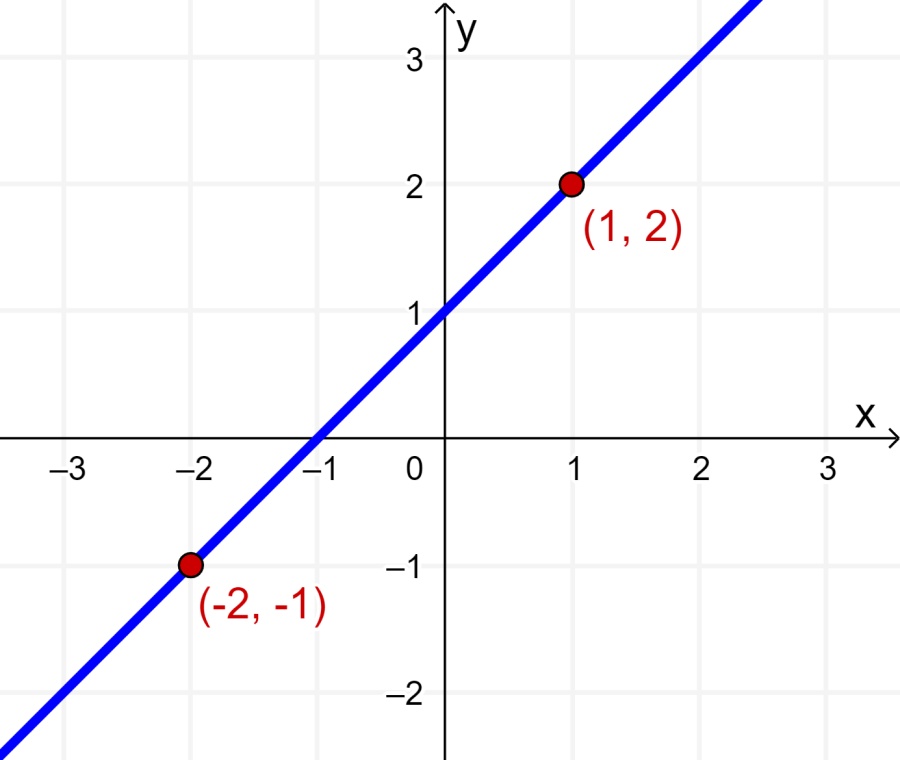
Uma vez que conhecemos dois pontos na linha, podemos usar a fórmula dois pontos na linha:
$latex y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$
$latex y-(-1)=\frac{2-(-1)}{1-(-2)}(x-(-2))$
$latex y+1=\frac{3}{3}(x+2)$
$latex y+1=1(x+2)$
$latex y+1=x+2$
$latex y=x+1$
EXERCÍCIO 3
Encontre a equação da reta que passa pelos pontos (-2, 2) e (2, 0).
Solução
A reta que passa por ambos os pontos é representada graficamente no plano seguinte:
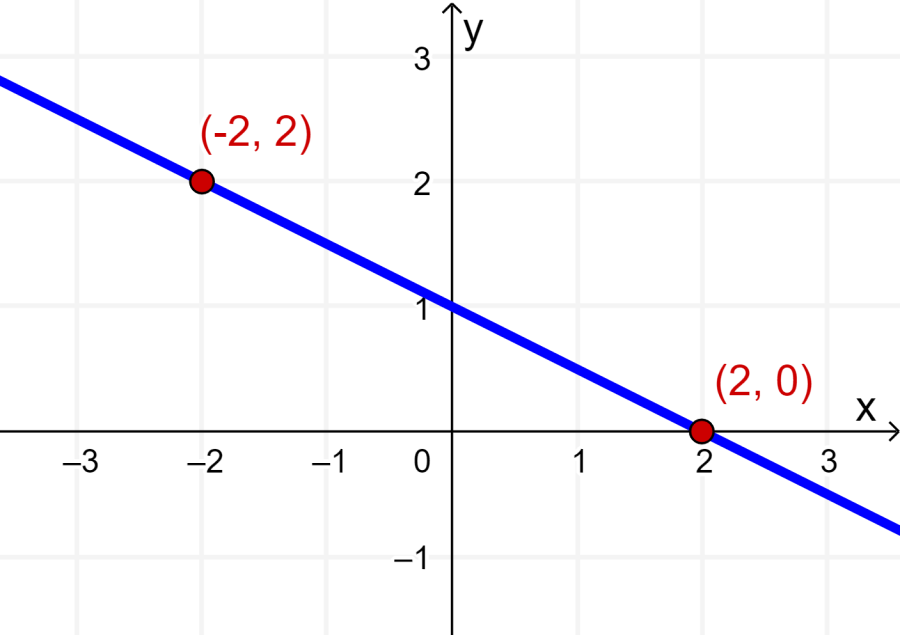
Temos que a reta passa pelos pontos (-2, 2) e (2, 0). Então, começamos encontrando o declive da reta:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{0-2}{2-(-2)}$
$latex m=\frac{-2}{4}=-\frac{1}{2}$
Agora, usamos o ponto (2, 0) para encontrar a interceptação em y:
$latex y=mx+b$
$latex 0= -\frac{1}{2}(2)+b$
$latex b= 1$
Portanto, a equação da reta é:
$latex y=-\frac{1}{2}x+1$
EXERCÍCIO 4
Encontre a equação da reta que passa pelos pontos (-1, 2) e (1, -2).
Solução
O gráfico a seguir mostra a reta que passa pelos pontos dados:
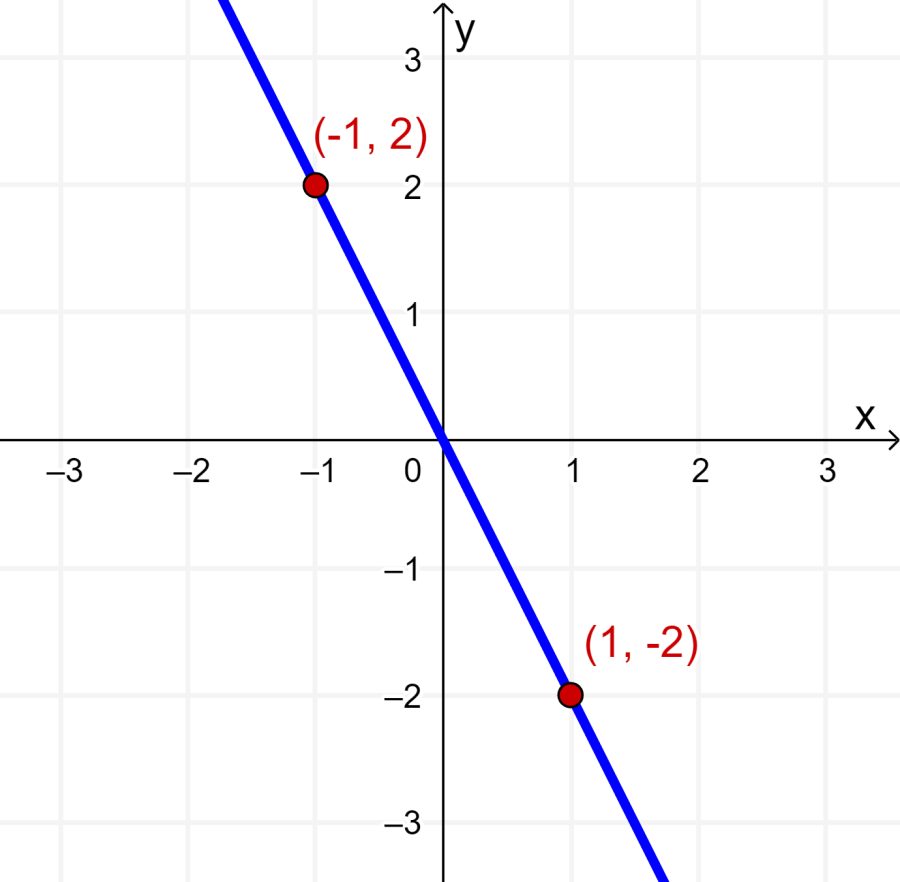
A reta passa pelos pontos (-1, 2) e (1, -2), então podemos usar a fórmula da reta:
$latex y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$
$latex y-2=\frac{-2-2}{1-(-1)}(x-(-1))$
$latex y-2=\frac{-4}{2}(x+1)$
$latex y-2=-2(x+1)$
$latex y-2=-2x-2$
$latex y=-2x$
EXERCÍCIO 5
Encontre a equação da reta que passa pelos pontos (-3, -2) e (3, 0).
Solução
Podemos ver a reta que passa pelos pontos dados no gráfico:
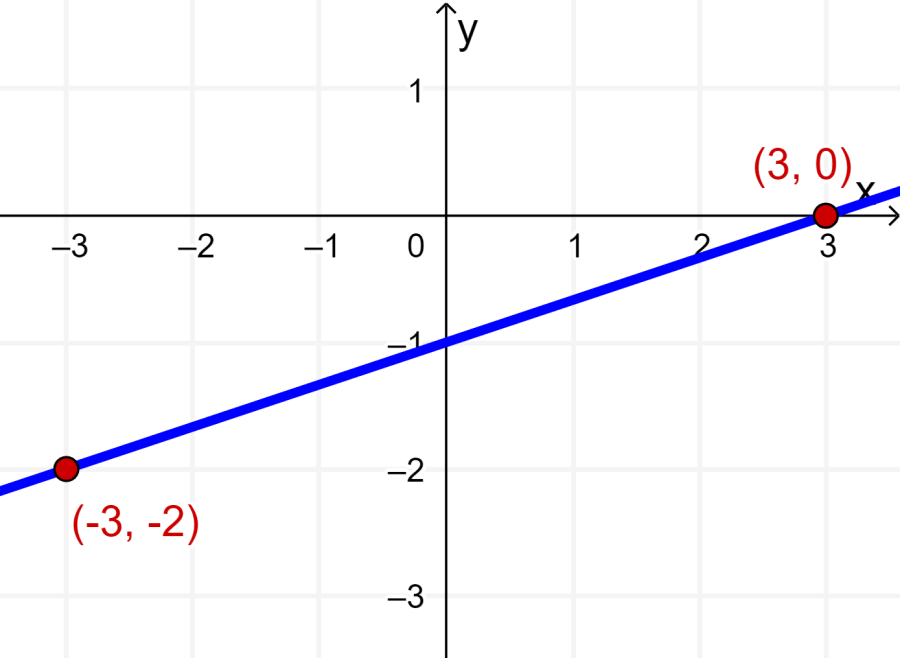
Os dois pontos são (-3, -2) e (3, 0). Então, temos que encontrar o declive da reta:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$latex m=\frac{0-(-2)}{3-(-3)}$
$latex m=\frac{2}{6}=\frac{1}{3}$
Agora, usamos o ponto (3, 0) para encontrar a interceptação emy:
$latex y=mx+b$
$latex 0= \frac{1}{3}(3)+b$
$latex b= -1$
Portanto, a equação da reta é:
$latex y=\frac{1}{3}x-1$
EXERCÍCIO 6
Encontre a equação da reta que passa pelos pontos (-3, 1) e (3, -3).
Solução
A seguir está o gráfico da reta que passa pelos pontos dados:
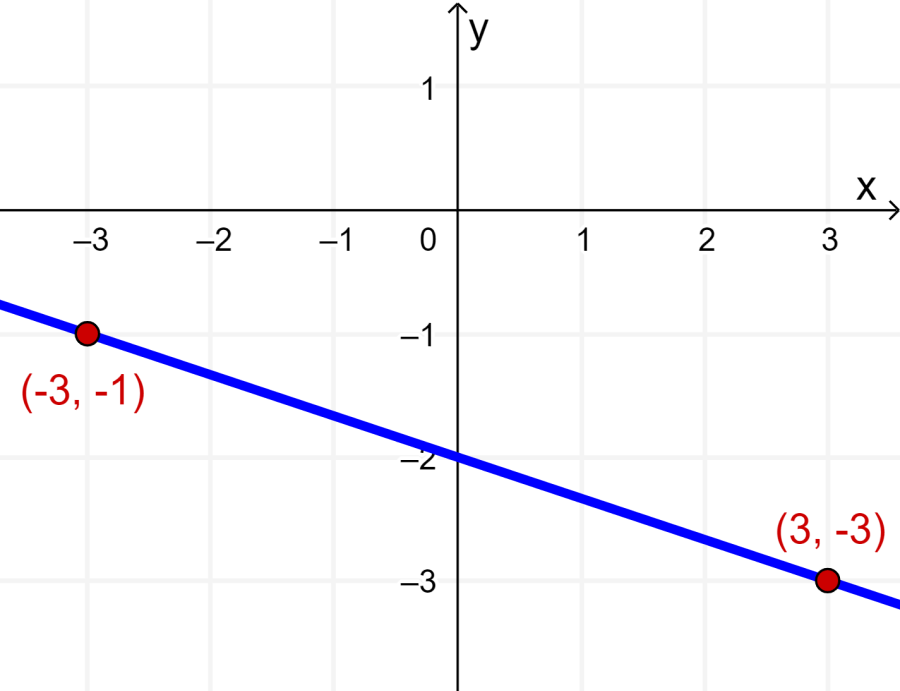
Temos os pontos (-3, -1) e (3, -3), então podemos usar a fórmula da reta:
$latex y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$
$latex y-(-1)=\frac{-3-(-1)}{3-(-3)}(x-(-3))$
$latex y+1=\frac{-2}{6}(x+3)$
$latex y+1=\frac{-1}{3}x-1$
$latex y=-\frac{1}{3}x-2$
Exercícios de equação da reta com dois pontos para resolver
Pratique e teste seus conhecimentos sobre a equação da reta que passa por dois pontos com os exercícios a seguir. Selecione uma resposta e verifique se você escolheu a resposta correta. Verifique os exercícios resolvidos acima se você tiver algum problema.
Veja também
Você quer aprender mais sobre retas? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
