Área e Perímetro dos Paralelogramos - Fórmulas e Exercícios

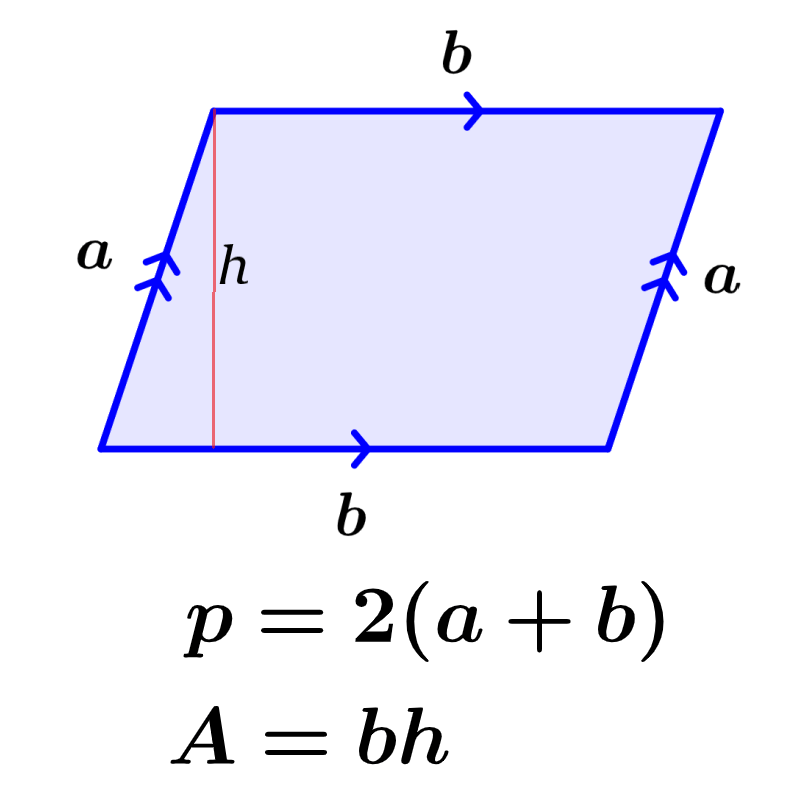
O perímetro de um paralelogramo representa o comprimento do contorno do paralelogramo. Por outro lado, a área é uma medida do espaço bidimensional ocupado pela figura. Podemos encontrar o perímetro do paralelogramo somando os comprimentos de seus quatro lados, e podemos encontrar a área multiplicando o comprimento de sua base por sua altura.

A seguir, aprenderemos tudo sobre o perímetro e a área de um paralelogramo. Conheceremos suas fórmulas e as aplicaremos para resolver alguns exercícios práticos.

GEOMETRIA

Fórmulas-para-o-perímetro-e-área-de-um-paralelogramo

Relevante para…

Aprender sobre o perímetro e a área dos paralelogramos.

Ver exercícios

Conteúdo

GEOMETRIA

Relevante para…

Aprender sobre o perímetro e a área dos paralelogramos.

Ver exercícios

freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_01" });

Como calcular o perímetro de um paralelogramo?

Para encontrar o perímetro de um paralelogramo, temos que somar os comprimentos de todos os seus lados. Considerando que os lados opostos de um paralelogramo têm o mesmo comprimento, podemos formar a seguinte fórmula:

$latex p=a+b+a+b$

$latex p=2a+2b$

$latex p=2(a+b)$

Calcular o perímetro de um paralelogramo com base e altura

Para calcular o perímetro de um paralelogramo usando sua base e altura, precisamos do ângulo entre sua altura e seu lado lateral, conforme mostrado no diagrama abaixo.

paralelogramo-com-altura-base-e-ângulo-lateral

Em um paralelogramo, os lados opostos são paralelos e iguais, e o perímetro do paralelogramo é definido como duas vezes o produto da base pela altura multiplicado pelo cosseno do ângulo:

$latex p=2(b+h~\cos(\theta))$

onde, $latex \theta$ é o ângulo entre a altura e o lado lateral do paralelogramo.

freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_d1" });

Como calcular a área de um paralelogramo?

Para calcular a área de um paralelogramo, podemos multiplicar o comprimento da base pela sua altura. Devemos considerar que a base e a altura do paralelogramo são perpendiculares entre si, enquanto o lado lateral do paralelogramo não é perpendicular à base.

Por exemplo, no diagrama abaixo, podemos ver que a altura do paralelogramo é diferente de seu lado lateral:

Assim, podemos usar a seguinte fórmula para encontrar a área de um paralelogramo:

$latex A=bh$

onde, b é o comprimento da base e h é a altura.

Calcular a área de um paralelogramo sem usar a altura

Podemos calcular a área de um paralelogramo sem sua altura se conhecermos os comprimentos de seus lados e o ângulo entre seus lados. Assim, usamos a seguinte fórmula:

$latex A=ab\sin(x)$

onde a e b são os comprimentos dos lados do paralelogramo e x é a medida do ângulo entre os lados.

Calcular a área de um paralelogramo usando diagonais

Podemos calcular a área de um paralelogramo quando conhecemos os comprimentos das diagonais e o ângulo de interseção das diagonais. Assim, usamos a seguinte fórmula:

$latex A=\frac{d_{1}\times d_{2}\sin(y)}{2}$

onde, $latex d_{1}, ~d_{2}$ são os comprimentos das diagonais e y é o ângulo de intersecção das diagonais.

freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_d2" });

Perímetro e área de um paralelogramo – Exercícios resolvidos

EXERCÍCIO 1

Encontre o perímetro de um paralelogramo com lados de 8 mm e 12 mm.

Solução

Temos os seguintes comprimentos:

Lado 1, $latex a=8$ mm
Lado 2, $latex b=12$ mm

Aplicando a fórmula do perímetro com esses valores, temos:

$latex p=2(a+b)$

$latex p=2(8+12)$

$latex p=2(20)$

$latex p=40$

O perímetro do paralelogramo é igual a 40 mm.

const alltoggles = document.getElementsByClassName("wp-block-ub-content-toggle-accordion-title-wrap"); const toggle1 = alltoggles[0]; toggle1.addEventListener('click', runToggle1); function runToggle1() { freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3" }); toggle1.removeEventListener('click', runToggle1); }

EXERCÍCIO 2

Encontre a área de um paralelogramo que tem bases de 12 m de comprimento e 11 m de altura.

Solução

Temos o seguinte:

Base, $latex b=12$m
Altura, $latex h=11$ m

Usando a fórmula da área com esses comprimentos, temos:

$latex A=bh$

$latex A=(12)(11)$

$latex A=132$

A área do paralelogramo é de 132 m².

const toggle2 = alltoggles[1]; toggle2.addEventListener('click', runToggle2); function runToggle2() { freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_2" }); toggle2.removeEventListener('click', runToggle2);}

EXERCÍCIO 3

Encontre o perímetro de um paralelogramo que tem lados de 15 cm e 17 cm.

Solução

Temos o seguinte:

Lado 1, $latex a=15$ cm
Lado 2, $latex b=17$ cm

Usando a fórmula do perímetro com esses valores, temos:

$latex p=2(a+b)$

$latex p=2(15+17)$

$latex p=2(32)$

$latex p=64$

O perímetro do paralelogramo é igual a 64 cm.

const toggle3 = alltoggles[2]; toggle3.addEventListener('click', runToggle3); function runToggle3() { freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_3" }); toggle3.removeEventListener('click', runToggle3);}

EXERCÍCIO 4

Encontre a área de um paralelogramo com uma base de 15 mm e uma altura de 20 mm.

Solução

Temos os seguintes comprimentos:

Base, $latex b=15$ mm
Altura, $latex h=20$ mm

Usando a fórmula da área com esses comprimentos, temos:

$latex A=bh$

$latex A=(15)(20)$

$latex A=300$

A área do paralelogramo é igual a 300 mm².

const toggle4 = alltoggles[3]; toggle4.addEventListener('click', runToggle4); function runToggle4() { freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_4" }); toggle4.removeEventListener('click', runToggle4);}

EXERCÍCIO 5

Se o perímetro de um paralelogramo mede 90 cm e um lado mede 21 cm, qual o comprimento do outro lado?

Solução

Temos o seguinte:

Perímetro, $latex p=90$ cm
Lado 1, $latex a=21$ cm

Neste caso, conhecemos o perímetro e queremos encontrar o comprimento do outro lado do paralelogramo. Então, usamos a fórmula do perímetro e resolvemos o lado que falta:

$latex p=2(a+b)$

$latex 90=2(21+b)$

$latex 90=42+2b$

$latex 2b=48$

$latex b=24$

O comprimento do outro lado é igual a 24 cm.

const toggle5 = alltoggles[4]; toggle5.addEventListener('click', runToggle5); function runToggle5() { freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_5" }); toggle5.removeEventListener('click', runToggle5);}

EXERCÍCIO 6

Qual é a área de um paralelogramo com lados de comprimentos 14 m e 12 m e o ângulo entre eles é 60°?

Solução

Temos o seguinte:

Lado 1, $latex a=14$ m
Lado 2, $latex b=12$ m
Ângulo, $latex x=60°$

Usando a segunda fórmula para a área de um paralelogramo, temos:

$latex A=ab\sin(x)$

$latex A=(14)(12)\sin(60°)$

$latex A=(168)(0,866)$

$latex A=145,5$

A área do paralelogramo é de 145,5 m².

const toggle6 = alltoggles[5]; toggle6.addEventListener('click', runToggle6); function runToggle6() { freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_6" }); toggle6.removeEventListener('click', runToggle6);}

EXERCÍCIO 7

Encontre o perímetro de um paralelogramo com uma altura de 10 m e uma base de 12 m se o ângulo entre a altura e o lado lateral for de 60°.

Solução

Temos o seguinte:

Altura, $latex h=10$ m
Base, $latex b=12$ m
Ângulo, $latex \theta=60°$

Usamos a segunda fórmula do perímetro e temos:

$latex p=2(b+h~\cos(\theta))$

$latex p=2(12+10~\cos(60°))$

$latex p=2(12+10(0,5))$

$latex p=2(12+5)$

$latex p=2(17)$

$latex p=34$

O perímetro do paralelogramo é igual a 34 m.

const toggle7 = alltoggles[6]; toggle7.addEventListener('click', runToggle7); function runToggle7() { freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_7" }); toggle7.removeEventListener('click', runToggle7);}

EXERCÍCIO 8

Um paralelogramo tem diagonais com comprimentos 10 mm e 9 mm. Se o ângulo de intersecção das diagonais é de 30°, qual é a sua área?

Solução

Temos o seguinte:

Diagonal 1, $latex d_{1}=10$ mm
Diagonal 2, $latex d_{2}=9$ mm
Ângulo, $latex y=30°$

Usando a fórmula da terceira área com as informações fornecidas, temos:

$$A=\frac{d_{1}\times d_{2}\sin(y)}{2}$$

$$A=\frac{10\times 9\sin(30°)}{2}$$

$$A=\frac{(90)(0,5)}{2}$$

$$A=\frac{45}{2}$$

$latex A=22,5$

A área do paralelogramo é igual a 22,5 mm².

const toggle8 = alltoggles[7]; toggle8.addEventListener('click', runToggle8); function runToggle8() { freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_8" }); toggle8.removeEventListener('click', runToggle8);}

EXERCÍCIO 9

Encontre o perímetro de um paralelogramo com uma altura de 20 cm e uma base de 15 cm se o ângulo entre a altura e o lado lateral for de 60°.

Solução

Temos o seguinte:

Altura, $latex h=20$ cm
Base, $latex b=15$ cm
Ângulo, $latex \theta=60°$

Usamos esses valores na segunda fórmula do perímetro e temos:

$latex p=2(b+h~\cos(\theta))$

$latex p=2(15+20~\cos(60°))$

$latex p=2(15+20(0,5))$

$latex p=2(15+10)$

$latex p=2(25)$

$latex p=50$

O perímetro do paralelogramo é igual a 50 cm.

const toggle9 = alltoggles[8]; toggle9.addEventListener('click', runToggle9); function runToggle9() { freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_9" }); toggle9.removeEventListener('click', runToggle9);}

EXERCÍCIO 10

A área de um paralelogramo é igual a 182 mm². Se sua altura é 13 mm, qual é o comprimento de sua base?

Solução

Temos os seguintes valores:

Área, $latex A=182$ mm²
Altura, $latex h=13$ mm

Usamos a fórmula da área com as informações fornecidas e resolvemos para a base, b:

$latex A=bh$

$latex 182=13b$

$latex b=14$

O comprimento da base é de 14 mm.

freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_d3" });

Perímetro e área de um paralelogramo – Exercícios para resolver

Encontre o perímetro de um paralelogramo com lados de comprimento 11 mm e 19 mm.

Escolha uma resposta

$latex p=30$ mm

$latex p=40$ mm

$latex p=60$ mm

$latex p=64$ mm

Encontre a área de um paralelogramo com 15 m de altura e 8 m de base.

Escolha uma resposta

$latex A=80~{{m}^2}$

$latex A=100~{{m}^2}$

$latex A=120~{{m}^2}$

$latex A=140~{{m}^2}$

freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_p1" });

Encontre o perímetro de um paralelogramo com lados de comprimento 17 cm e 21 cm.

Escolha uma resposta

$latex p=68$ cm

$latex p=76$ cm

$latex p=82$ cm

$latex p=84$ cm

Encontre a área de um paralelogramo que tem 21 cm de altura e 22 cm de base.

Escolha uma resposta

$latex A=422~{{cm}^2}$

$latex A=462~{{cm}^2}$

$latex A=482~{{cm}^2}$

$latex A=492~{{cm}^2}$

freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_p2" });

Qual é o perímetro de um paralelogramo com uma altura de 8 m, uma base de 12 m e o ângulo entre a altura e o lado lateral é de 60°?

Escolha uma resposta

$latex p=20$ m

$latex p=32$ m

$latex p=36$ m

$latex p=40$ m

Encontre a área de um paralelogramo com diagonais de 13m e 15m e o ângulo entre as diagonais é 30°.

Escolha uma resposta

$latex A=42,5~{{m}^2}$

$latex A=48,75~{{m}^2}$

$latex A=97,5~{{m}^2}$

$latex A=195~{{m}^2}$

freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_3", slotId: "neurochispas_leaderboard_3_d4" });

Veja também

Interessado em aprender mais sobre perímetros e áreas de figuras geométricas? Você pode olhar para estas páginas:

Jefferson Huera Guzman

Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.

.author-box {margin: 70px 0; padding: 30px; background-color: #f9fcff; border-radius: 15px; box-shadow: 0px 0px 10px #ccc; max-width:1100px; margin-left:auto !important; margin-right:0px !important; } .author-box img {margin:auto; border-radius: 50%;} .author-box h3 {margin-top: 20px; font-size:19px;} .author-box p {margin: 10px 0; text-align:left; } .author-box a {display: inline-block; margin-right: 10px; color: black; text-decoration: none;} { "@context": "http://schema.org", "@type": "Person", "name": "Jefferson Huera Guzman", "image": "https://br.neurochispas.com/wp-content/uploads/2021/05/imagen-autor.png", "url": "https://br.neurochispas.com/jefferson-huera-guzman", "description": "Jefferson é o principal autor e administrador do Neurochispas.com.", "sameAs": [ "https://www.instagram.com/jeffersonhuera/", "https://www.jeffersonhuera.com/"], "email": "[email protected]", "worksFor": { "@type": "Organization", "name": "Interacti Digital LLC"}, "alumniOf": { "@type": "CollegeOrUniversity", "name": "The University of Manchester"}, "knowsAbout": [ "Algebra", "Calculus", "Geometry", "Mathematics", "Physics"] }

Aprenda matemática com nossos recursos adicionais em diferentes tópicos

APRENDER MAIS

freestar.config.enabled_slots.push({ placementName: "neurochispas_leaderboard_1", slotId: "neurochispas_leaderboard_1_30" });

GEOMETRIA

GEOMETRIA

Como calcular o perímetro de um paralelogramo?

Calcular o perímetro de um paralelogramo com base e altura

Como calcular a área de um paralelogramo?

Calcular a área de um paralelogramo sem usar a altura

Calcular a área de um paralelogramo usando diagonais

Perímetro e área de um paralelogramo – Exercícios resolvidos

EXERCÍCIO 1

Solução

EXERCÍCIO 2

Solução

EXERCÍCIO 3

Solução

EXERCÍCIO 4

Solução

EXERCÍCIO 5

Solução

EXERCÍCIO 6

Solução

EXERCÍCIO 7

Solução

EXERCÍCIO 8

Solução

EXERCÍCIO 9

Solução

EXERCÍCIO 10

Solução

Perímetro e área de um paralelogramo – Exercícios para resolver

Encontre o perímetro de um paralelogramo com lados de comprimento 11 mm e 19 mm.

Encontre a área de um paralelogramo com 15 m de altura e 8 m de base.

Encontre o perímetro de um paralelogramo com lados de comprimento 17 cm e 21 cm.

Encontre a área de um paralelogramo que tem 21 cm de altura e 22 cm de base.

Qual é o perímetro de um paralelogramo com uma altura de 8 m, uma base de 12 m e o ângulo entre a altura e o lado lateral é de 60°?

Encontre a área de um paralelogramo com diagonais de 13m e 15m e o ângulo entre as diagonais é 30°.

Veja também

Jefferson Huera Guzman

Aprenda matemática com nossos recursos adicionais em diferentes tópicos

INFORMAÇÃO

RECURSOS

SUPORTE