O perímetro de um triângulo equilátero é o comprimento do contorno do triângulo. Por outro lado, a área é uma medida do espaço ocupado pelo triângulo. Podemos encontrar o perímetro do triângulo equilátero somando os comprimentos de seus três lados, e podemos encontrar sua área multiplicando o comprimento de sua base por sua altura e dividindo por 2.
A seguir, aprenderemos tudo sobre o perímetro e a área de um triângulo equilátero. Conheceremos suas fórmulas e as aplicaremos para resolver alguns exercícios práticos.
GEOMETRIA
Relevante para…
Aprender sobre o perímetro e a área de um triângulo equilátero.
GEOMETRIA
Relevante para…
Aprender sobre o perímetro e a área de um triângulo equilátero.
Como calcular o perímetro de um triângulo equilátero?
Para calcular o perímetro de um triângulo equilátero, temos que somar os comprimentos de seus três lados. Lembrando que um triângulo equilátero tem todos os lados do mesmo comprimento, basta multiplicar o comprimento de um dos lados por 3:
| $latex p=3a$ |
onde, a é o comprimento de um lado do triângulo.
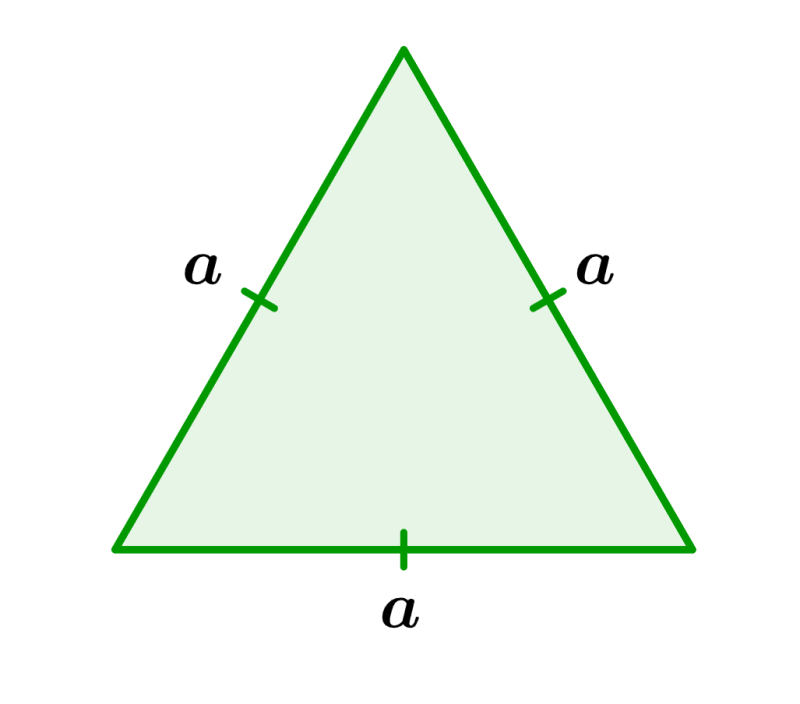
Isso significa que só precisamos saber o comprimento de um dos lados do triângulo equilátero para calcular seu perímetro.
Como calcular a área de um triângulo equilátero?
Para calcular a área de qualquer triângulo, podemos multiplicar sua base por sua altura e dividir por 2. No caso de triângulos equiláteros, podemos usar a seguinte fórmula para calcular sua área:
| $latex A= \frac{ \sqrt{3}}{4}{{a}^2}$ |
onde, a é o comprimento de um dos lados do triângulo equilátero.
Prova da fórmula para a área de um triângulo equilátero
Para provar a fórmula da área de um triângulo equilátero, vamos usar o seguinte diagrama, onde desenhamos uma bissetriz perpendicular à base com altura h:
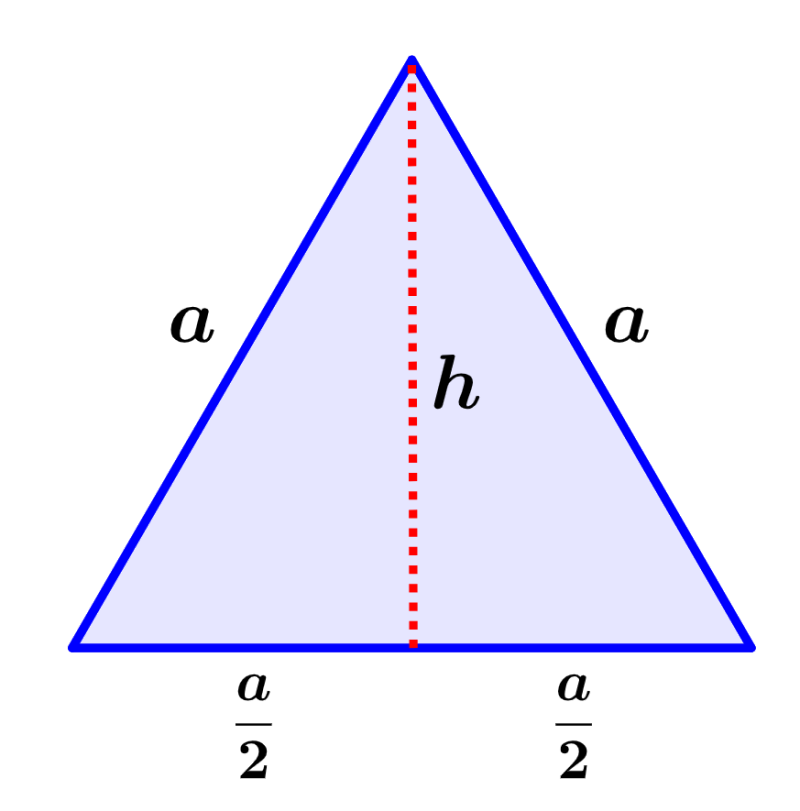
Lembramos que a área de qualquer triângulo pode ser calculada com a seguinte fórmula:
$latex \text{Área}= \frac{1}{2} \times \text{base} \times \text{altura}$
Aqui, a base é igual a “a” e a altura é igual a “h”.
Usando o teorema de Pitágoras para calcular a altura, temos:
$latex {{a}^2}={{h}^2}+{{( \frac{a}{2})}^2}$
⇒ $latex {{h}^2}={{a}^2}- \frac{{{a}^2}}{4}$
⇒ $latex {{h}^2}=\frac{3{{a}^2}}{4}$
⇒ $latex h=\frac{\sqrt{3}~a}{2}$
Agora que temos uma expressão para h, podemos usá-la na fórmula da área de um triângulo:
$latex \text{Área}= \frac{1}{2} \times \text{base} \times \text{altura}$
$latex A=\frac{1}{2}\times a \times \frac{\sqrt{3}~a}{2}$
⇒ $latex A=\frac{\sqrt{3}~{{a}^2}}{4}$
Área e perímetro de um triângulo equilátero – Exercícios resolvidos
EXERCÍCIO 1
Encontre o perímetro de um triângulo equilátero com lados de comprimento 5 mm.
Solução
Usamos a fórmula do perímetro com o valor $latex a=5$. Então temos:
$latex p=3a$
$latex p=3(5)$
$latex p=15$
O perímetro do triângulo equilátero é igual a 15 mm.
EXERCÍCIO 2
Qual é a área de um triângulo equilátero com lados de 10 cm de comprimento?
Solução
Usamos a fórmula da área com comprimento a=10:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex A= \frac{ \sqrt{3}}{4}({{10}^2})$
$latex A= \frac{ \sqrt{3}}{4}(100)$
$latex A=43,3$
A área do triângulo equilátero é igual a 43,3 cm².
EXERCÍCIO 3
Encontre o perímetro de um triângulo equilátero com lados de 8 cm de comprimento.
Solução
Usando o valor $latex a=8$ na fórmula do perímetro, temos:
$latex p=3a$
$latex p=3(8)$
$latex p=24$
O perímetro do triângulo equilátero é igual a 24 cm.
EXERCÍCIO 4
Encontre a área de um triângulo equilátero com lados de comprimento 14 cm.
Solução
Aplicando a fórmula da área com o comprimento dado, temos:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex A= \frac{ \sqrt{3}}{4}({{14}^2})$
$latex A= \frac{ \sqrt{3}}{4}(196)$
$latex A=84,87$
A área do triângulo equilátero é igual a 84,87 cm².
EXERCÍCIO 5
Qual é o perímetro de um triângulo equilátero com lados de 15 cm de comprimento?
Solução
Aplicando a fórmula do perímetro com o valor $latex a=15$:
$latex p=3a$
$latex p=3(15)$
$latex p=45$
O perímetro do triângulo é igual a 45 cm.
EXERCÍCIO 6
Qual é a área de um triângulo equilátero com lados com comprimento de 15 m?
Solução
Usamos o comprimento $latex a=15$ na fórmula da área:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex A= \frac{ \sqrt{3}}{4}({{15}^2})$
$latex A= \frac{ \sqrt{3}}{4}(225)$
$latex A=97,43$
A área do triângulo equilátero é igual a 97,43 m².
EXERCÍCIO 7
Encontre o comprimento dos lados de um triângulo equilátero com um perímetro de 39 m.
Solução
Neste exercício, conhecemos o perímetro do triângulo e temos que encontrar o comprimento de um lado. Então, usamos a fórmula do perímetro e resolvemos para a:
$latex p=3a$
$latex 39=3a$
$latex a=13$
Os lados do triângulo têm um comprimento de 13 m.
EXERCÍCIO 8
Encontre o comprimento dos lados de um triângulo equilátero com uma área de 35,07 m².
Solução
Neste caso, conhecemos a área e precisamos encontrar o comprimento dos lados. Então, usamos a fórmula da área e resolvemos para a:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex 35,07= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex 35,07=0,433{{a}^2}$
$latex {{a}^2}=81$
$latex a=9$
Os lados do triângulo têm um comprimento de 9 m.
EXERCÍCIO 9
Encontre o comprimento dos lados de um triângulo equilátero com um perímetro de 102 mm.
Solução
Vamos usar a fórmula do perímetro com o valor $latex p=102$ e resolver para a:
$latex p=3a$
$latex 102=3a$
$latex a=34$
O comprimento de um lado do triângulo é 34 mm.
EXERCÍCIO 10
Encontre o comprimento dos lados de um triângulo equilátero com uma área de 73,18 m².
Solução
Usamos a fórmula da área com o valor dado e resolvemos para a:
$latex A= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex 73,18= \frac{ \sqrt{3}}{4}{{a}^2}$
$latex 73,18=0,433{{a}^2}$
$latex {{a}^2}=169$
$latex a=13$
O comprimento dos lados do triângulo é 13 m.
Área e perímetro de um triângulo equilátero – Exercícios resolvidos
Veja também
Interessado em aprender mais sobre perímetros e áreas de figuras geométricas? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
