Matrizes são comumente usadas em matemática e outras áreas para representar dados ou resolver equações. Para somar e subtrair matrizes, basta somar e subtrair os elementos correspondentes em cada posição.
Neste artigo, aprenderemos as etapas necessárias para adicionar e subtrair matrizes 3×3, fornecer vários exemplos com soluções e oferecer problemas práticos para ajudá-lo a desenvolver suas habilidades.
ÁLGEBRA LINEAR
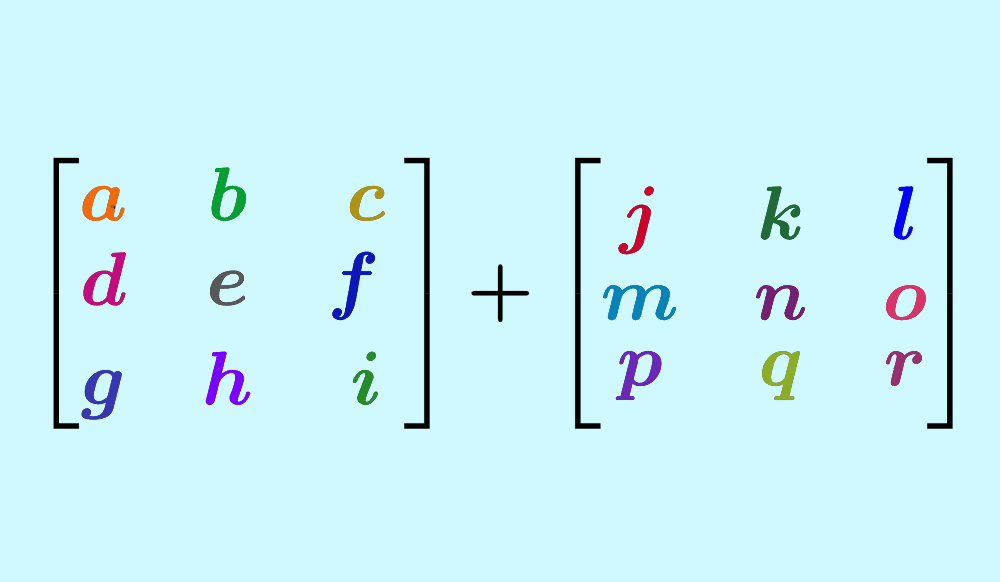
Relevante para…
Aprender a somar e subtrair matrizes 3×3 com exercícios.
ÁLGEBRA LINEAR
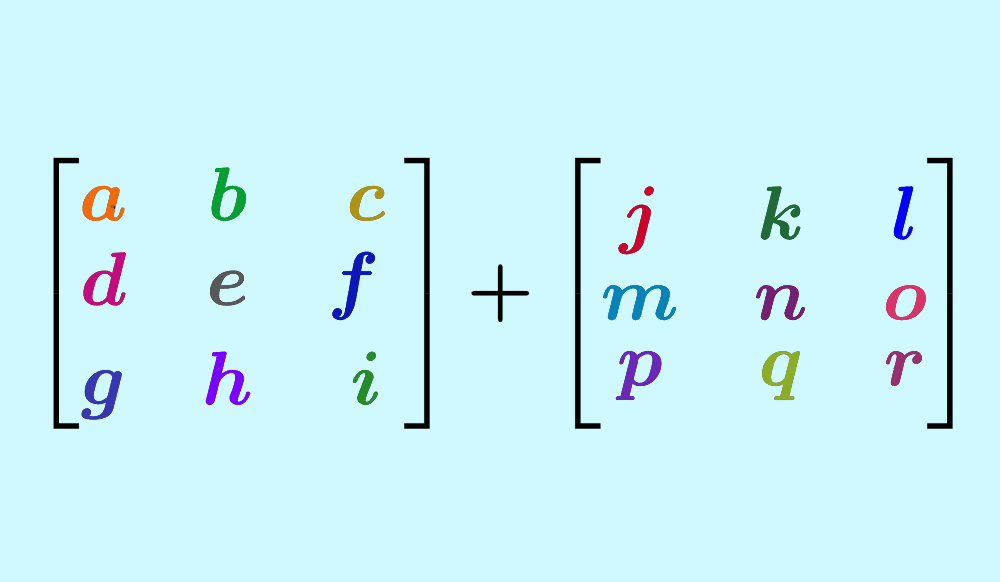
Relevante para…
Aprender a somar e subtrair matrizes 3×3 com exercícios.
Como adicionar e subtrair matrizes 3×3?
Para adicionar e subtrair matrizes 3×3 temos que adicionar ou subtrair cada elemento correspondente de duas, ou mais matrizes do mesmo tamanho.
Podemos adicionar ou subtrair matrizes 3×3 seguindo os seguintes passos:
Passo 1: Escreva as duas matrizes que deseja adicionar lado a lado com um símbolo de mais (+) ou subtração (-) entre elas.
Passo 2: Adicione ou subtraia cada elemento correspondente das duas matrizes.
Por exemplo, adicione o primeiro elemento da primeira matriz ao primeiro elemento da segunda matriz e assim por diante. Escreva o resultado em uma nova matriz do mesmo tamanho.
Passo 3: Repita o passo 2 para cada elemento correspondente até adicionar ou subtrair todos os elementos.
Por exemplo, suponha que temos as seguintes matrizes 3×3:
$$A = \begin{bmatrix} 1& 2 & 3 \\ 7& 8&9 \\ 5& 4&6\end{bmatrix}$$
$$B = \begin{bmatrix} 4& 5 & 6 \\ 2& 3&1 \\ 0& 1&2\end{bmatrix}$$
Somamos as matrizes para obter A+B:
$$A+B = \begin{bmatrix} 1+4& 2+5 & 3+6 \\ 7+2& 8+3&9+1 \\ 5+0& 4+1&6+2\end{bmatrix}$$
$$A+B = \begin{bmatrix} 5& 7&9\\ 9& 11 & 10 \\ 5& 5 &8\end{bmatrix}$$
Subtraímos as matrizes para obter A-B
$$A+B = \begin{bmatrix} 1-4& 2-5 & 3-6 \\ 7-2& 8-3&9-1 \\ 5-0& 4-1&6-2\end{bmatrix}$$
$$A+B = \begin{bmatrix} -3& -3&-3\\ 5& 5 & 8 \\ 5& 3 &4\end{bmatrix}$$
Nota: Tenha em mente que você só pode adicionar ou subtrair matrizes do mesmo tamanho, portanto, neste caso, ambas as matrizes devem ser matrizes 3×3.
Exercícios resolvidos de adição e subtração de matrizes 3×3
EXERCÍCIO 1
Qual é a soma das seguintes matrizes?
$$ A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$
$$ B= \begin{bmatrix} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix} $$
Solução
Podemos resolver este exercício adicionando os elementos correspondentes de ambas as matrizes em cada posição:
$$ A+B= \begin{bmatrix} 1+0 & 2+1 & 3+2 \\ 4+3 & 5+4 & 6+5 \\ 7+6 & 8+7 & 9+8 \end{bmatrix}$$
$$A+B = \begin{bmatrix} 1 & 3 & 5 \\ 7 & 9 & 11 \\ 13 & 15 & 17 \end{bmatrix} $$
EXERCÍCIO 2
Encontre a subtração AB das seguintes matrizes.
$$ A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$
$$ B= \begin{bmatrix} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix} $$
Solução
Este exercício nos pede para subtrair a matriz B da matriz A. Em seguida, subtraímos os elementos correspondentes:
$$ A-B= \begin{bmatrix} 1-0 & 2-1 & 3-2 \\ 4-3 & 5-4 & 6-5 \\ 7-6 & 8-7 & 9-8 \end{bmatrix}$$
$$A-B = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} $$
EXERCÍCIO 3
Determine o resultado da subtração B-A.
$$ A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$
$$ B= \begin{bmatrix} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix} $$
Solução
Para resolver este exercício, devemos considerar que a subtração B-A não é igual à subtração A-B. Neste caso, subtraímos a matriz A da matriz B:
$$ B-A= \begin{bmatrix} 0-1 & 1-2 & 2-3 \\ 3-4 & 4-5 & 5-6 \\ 6-7 & 7-8 & 8-9 \end{bmatrix}$$
$$B-A = \begin{bmatrix} -1 & -1 & -1 \\ -1 & -1 & -1 \\ -1 & -1 & -1 \end{bmatrix} $$
EXERCÍCIO 4
Qual é o resultado da adição e subtração (A-B) das seguintes matrizes?
$$A = \begin{bmatrix} 6 & 3 & 2 \\ -3 & 5 & 3 \\ -5 & 2 & -9 \end{bmatrix} $$
$$B = \begin{bmatrix} -3 & 7 & 8 \\ 11 & -8 & 5 \\ -5 & 8 & 12 \end{bmatrix} $$
Solução
Quando somamos as matrizes, temos:
$$A+B = \begin{bmatrix} 6-3 & 3+7 & 2+8 \\ -3+11 & 5-8 & 3+5 \\ -5-5 & 2+8 & -9+12 \end{bmatrix} $$
$$A+B = \begin{bmatrix} 3 & 10 & 10 \\ 8 & -3 & 2 \\ -10 & 10 & 3 \end{bmatrix} $$
Quando subtraímos as matrizes, temos:
$$A-B = \begin{bmatrix} 6+3 & 3-7 & 2-8 \\ -3-11 & 5+8 & 3-5 \\ -5+5 & 2-8 & -9-12 \end{bmatrix} $$
$$A-B = \begin{bmatrix} 9 & -4 & -6 \\ -14 & 13 & -2 \\ 0 & -6 & -21 \end{bmatrix} $$
EXERCÍCIO 5
Determine a soma e a diferença B-A das seguintes matrizes.
$$A = \begin{bmatrix} 12 & -13 & 9 \\ -8 & 15 & 13 \\ -6 & -14 & 8 \end{bmatrix} $$
$$A = \begin{bmatrix} 6 & -8 & 12 \\ 11 & 13 & -7 \\ 5 & 12 & -9 \end{bmatrix} $$
Solução
Somando as matrizes A e B fornecidas, temos:
$$A+B = \begin{bmatrix} 12+6 & -13-8 & 9+12 \\ -8+11 & 15+13 & 13-7 \\ -6+5 & -14+12 & 8-9 \end{bmatrix} $$
$$A+B = \begin{bmatrix} 18 & -21 & 21 \\ 3 & 28 & 6 \\ -1 & -2 & 1 \end{bmatrix} $$
O resultado da subtração B-A é
$$B-A = \begin{bmatrix} 6-12 & -8+13 & 12-9 \\ 11+8 & 13-15 & -7-13 \\ 5+6 & 12+14 & -9-8 \end{bmatrix} $$
$$A+B = \begin{bmatrix} -6& 5 & 3 \\ 19 & -2 & -20 \\ 11 & 26 & -17 \end{bmatrix} $$
EXERCÍCIO 6
Se tivermos as seguintes matrizes, quais são os valores de $latex a$ e $latex b$.
$$A = \begin{bmatrix} 7 & 11 & -12 \\ 9 & 23 & 11 \\ -8 & -6 & a \end{bmatrix} $$
$$B = \begin{bmatrix} 4 & -8 & 7 \\ 14 & b & -7 \\ 5 & 2 & -9 \end{bmatrix} $$
$$A+B = \begin{bmatrix} 11 & 3 & -5 \\ 23 & 11 & 4 \\ 3 & -4 & -2 \end{bmatrix} $$
Solução
Neste exercício sabemos a soma das matrizes e temos que encontrar os valores de $latex a$ e $latex b$.
Para isso, podemos formar equações com a soma em cada posição do elemento requerido:
$latex a+(-9)=-2$
$latex 23+b=11$
Resolvendo as equações, temos:
$latex a=7$
$latex b=-12$
Exercícios de adição e subtração de matrizes 3×3 para resolver
Escreva a resposta na caixa de entrada.
Veja também
Interessado em aprender mais sobre matrizes? Você pode consultar estas páginas:
–
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
